2. Нормальное распределение.

Случайная величина называется распределенной по нормальному закону, если она имеет плотность вероятности следующего вида:

,

здесь постоянные величины, смысл которых станет ясен при дальнейшем рассмотрении. Пока же будем называть их параметрами кривой,- основание натурального логарифма ()

График этой функции приведен на рисунке.

Часто эту кривую называют колоколом за ее форму. Отметим ее основные особенности. Кривая симметрична. Центр симметрии, и это легко доказать, есть точка . Значит параметрмож­но назвать центром симметрии. При возрастании величины, например, для, кривая, не меняя своей формы будет смещаться вдоль оси абсцисс вправо.

Ветви кривой не пересекают ось абсцисс, а лишь асимптотически приближаются к ней, то есть

Исследование заданной функции с помощью производных, а именно нахождение максимума и точек перегиба (что рекомендуется проделать самостоятельно) дает следующие результаты:

1. 

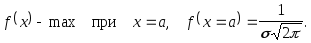
2. Координаты точек перегиба .

Параметр часто называют параметром ширины кривой. При возрастанииформа кривой будет изменяться. Во-первых, будут смещаться точки перегиба, разбегаясь от центра симметрии. Во-вторых, будет уменьшаться высота кривой, так как она обратно пропорциональна. В-третьих, и это очень важно, нужно вспомнить условие нормировки для непрерывной случайной величины:

Это значит, что площадь под кривой должна сохраняться постоянной, равной единице. Следовательно, если вершина колокола опускается, то ветви будут подниматься. Вот пример двух кривых Гаусса для разных . Пусть

3. Числовые характеристики непрерывной случайной величины, распределенной по нормальному закону.

1. Математическое ожидание.

Вспомним общую формулу для .

Подставим вместо функцию Гаусса:

.

Чтобы взять этот интеграл, введем замену переменной:

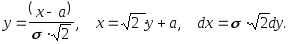
Сократив на и представив интеграл от суммы функций, как сумму интегралов, имеем:

.

Решая первый интеграл, получаем:

.

При подстановке значений верхнего и нижнего пределов интеграл обращается в ноль.

Обратимся ко второму интегралу. Функция вида - есть табличный интеграл.

В результате интегрирования мы пришли к интересному и важному результату: .

2. Дисперсия.

.

Подставляя под интеграл функцию Гаусса и пользуясь только что полученным соотношением , имеем:

Дисперсия была введена как мера рассеяния всех значений вблизи математического ожидания. Оказалось, что параметр ширины кривой играет ту же роль. Его называют среднеквадратичным отклонением . Пользоваться величиной для оценки меры отклонения гораздо удобнее, так как размерности самой случайной величины, ее математического ожидания и средне­квад­ра­тич­но­го отклонения совпадают. Например, если случайная величина это длина, тоиз­ме­ряются в метрах, в то время как дисперсия измеряется в метрах квадратных.

4. Нормированные случайные величины. Нормальная функция распределения.

В прикладных задачах при изучении случайных непрерывных величин чаще всего встре­ча­ют­ся ситуации, когда необходимо проводить сравнение поведения нескольких случайных ве­ли­чин, либо рассчитывать вероятности попадания случайной величины в заданный интервал на чис­ло­вой оси. Возникает потребность привести сравниваемые случайные величины к одному уров­ню, стандартизировать их. Тогда не нужно будет сравнивать метры и килограммы, градусы и мил­ли­метры ртутного столба. С этой целью было предложено нормировать случайные величины с помощью линейного преобразования

.

Нормированная случайная величина обладает целым рядом ценных качеств. Во-первых, она без­раз­мерна. Во-вторых, ее математическое ожидание равно нулю. В-третьих, ее сред­не­квад­ратичное отклонение равно 1,

Плотность вероятности нормированной случайной величины будет соответственно:

.

А функция распределения равна:

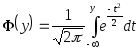
и называется нормальной функцией распределения.

Вероятность попадания случайной величины на заданный отрезок определяется соот­но­ше­ни­ем:.

Вспомним, что вероятность попадания случайной величины на заданный отрезок численно рав­на площади под кривой. Как она будет выглядеть для нормированной случайной вели­чи­ны?

Приведем фрагмент таблицы для нормальной функции распределения

Интервал	Вероятность

Значения функции распределения отдос шагом 0,01 можно найти в таблицах математической статистики.

Перечислим свойства нормальной функции распределения.

Последнее свойство широко используется, если требуется найти значение нормальной функции рас­пределения для отрицательных значений нормированной случайной величины. В таблицах ма­те­матической статистики обычно приводятся значения только для положительных.

График нормальной функции распределения имеет следующий вид:

21