5. Непрерывная случайная величина.

Случайную величину называют непрерывной, если она может принимать все значения из некоторого конечного или бесконечного интервала. Для непрерывной случайной величины нельзя построить ряд распределения. Непрерывная случай­ная величина имеет бесчисленное множество возможных значений сплошь заполняющих неко­то­рый промежуток (так называемое несчетное множество). Составить таблицу, в которой были бы пе­речислены все возможные значения такой случайной величины, невозможно. Каждое отдельное зна­чение непрерывной случайной величины обычно не обладает никакой отличной от нуля веро­ят­ностью. Однако, различные области возможных значений случайной величины все же не явля­ют­ся одинаково вероятными, и для непрерывной величины существует распределение вероят­нос­тей, хотя и не в том смысле, как для дискретной.

Закон распределения непрерывной случайной величины может быть задан в виде:

• интервальной таблицы;

• графика;

• функции распределения;

• плотности распределения.

Закон распределения в виде интервальной таблицы частот:

		...
		...

Здесь относительное число значений, попавших в интервал, или частота попадания в заданный интервал.

График распределения - гистограмма .

Функция распределения.

Для количественной характеристики распределения вероятностей непрерывной случайной величины удобно воспользоваться не вероятностью события , а вероятностью.

Здесь под понимается текущая переменная. Тогда функция распределения может быть определена следующим образом:

Функция распределения самая универсальная характеристика случайной величины.

График функции распределения :

В пределе при уменьшении длины интервала от ступенчатой кривой переходим к плавнойS-об­разной линии

Свойства функции распределения:

Еще одной формой задания закона распределения непрерывной случайной величины является фун­кция плотности распределения. Но прежде, чем ее рассмотреть, остановимся на следующем вопросе.

6. Вероятность попадания непрерывной случайной величины на заданный участок числовой оси.

Имеем участок числовой оси в пределах от до. Рассмотрим отдельно три события?

Событие , которое состоит в том, что.

Событие , которое состоит в том, что.

Событие , которое состоит в том, что.

По теореме сложения вероятностей для получаем:

Оказывается, вероятность попадания случайной величины на заданный участок числовой оси равна приращению функции распределения на этом участке.

Найдем теперь

.

Это есть не что иное как производная функции распре­де­ле­ния. Обозначим ее и назовем плотностью распределения. Плотность распре­де­ле­ния, так же как и функция распределения, есть одна из форм задания закона распределения для не­пре­рывной случайной величины. В противоположность функции распределения, эта форма не яв­ля­ется универсальной, она существует только для непрерывной случайной величины.

Рас­смотрим непрерывную случайную величину с плотностью распределения и эле­мен­тар­ный участок, примыкающий к точке.

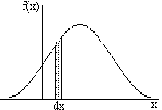
Вероятность попадания случайной величины на этот элементарный участок (с точностью до бес­ко­нечно малых высшего порядка) равна . Эту величинупринято называть эле­мен­том вероятности. Геометрически это заштрихованная на рисунке площадь элементарного пря­мо­угольника, опирающегося на отрезок.Если увеличить область на числовой оси до некоторого интервала, то вероятность попа­да­ния на этот отрезок будет равна сумме эле­ме­н­тов вероятности на всем участке, то есть интегралу

.

Геометрически это опять будет площадь.

Как можно представить функцию распределения на этом графике?

Сначала запишем формулу для функции распределения: .

Геометрический смысл функции распределения это площадь, ограниченная сверху графиком функции, а снизуосью абсцисс, справавертикальным отрезком.

Условие нормировки для непрерывной случайной величины.

Чему равна вероятность попасть на любой участок числовой оси.? То есть при нахождении такой вероятности мы должны взять интеграл в пределах от -до +. А геометрически это будет площадь под всей кривой..