Дисперсия дискретной случайной величины.

1.Целесообразность введения числовой характеристики рассеяния случайной величины. Отклонение случайной величины от её математического ожидания.

Легко указать такие случайные величины, которые имеют одинаковые математические ожидания, но различные возможные значения. Рассмотрим, например, дискретные случайные величины X и Y, заданные следующими законами распределения:

X	– 0,01	0,01	Y	– 100	100
р	0,5	0,5	g	0,5	0,5

Найдем математические ожидания этих величин:

М(Х) = – 0,010,5 + 0,010,5 = 0,

М(Y) = – 1000,5 + 1000,5 = 0.

Здесь математические ожидания обеих величин одинаковы, а возможные значения различны, причем X имеет возможные значения, близкие к математическому ожиданию, а Y – далекие от своего математического ожидания. Таким образом, зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она может принимать, ни о том, как они рассеяны вокруг математического ожидания. Другими словами, математическое ожидание полностью случайную величину не характеризует.

По этой причине наряду с математическим ожиданием вводят и другие числовые характеристики. Так, например, для того чтобы оценить, как рассеяны возможные значения случайной величины вокруг ее математического ожидания, пользуются, в частности, числовой характеристикой, которую называют дисперсией. Прежде чем перейти к определению и свойствам дисперсии, введем понятие отклонения случайной величины от ее математического ожидания.

Отклонением называют разность между случайной величиной и ее математическим ожиданиям.

Пусть закон распределения X известен:

X	x1	x2	…	xn
р	р1	р2	…	pn

Напишем закон распределения отклонения. Для того чтобы отклонение приняло значение х₁ – М(X), достаточно, чтобы случайная величина приняла значение х₁. Вероятность же этого события равна р₁; следовательно, и вероятность того, что отклонение примет значение х₁ – М(X), также равна р₁. Аналогично обстоит дело и для остальных возможных значений отклонения.

Таким образом, отклонение имеет следующий закон распределения:

X – М(X)	x1 – М(X)	x2 – М(X)	…	xn – М(X)
р	р1	р2	…	pn

Приведем важное свойство отклонения, которое используется далее.

Теорема. Математическое ожидание отклонения равно нулю:

М[X – М(X)] = 0.

2.Дисперсия дискретной случайной величины. Формула вычисления дисперсии.

Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величиныот ее математического ожидания:

D(X) = М(X ²)– М ²(X).

3.Свойства дисперсии.

• Свойство 1. Дисперсия постоянной величины С равна нулю:

D(С) = 0.

• Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:

D(СX) = C² D(X).

• Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:

D(X + Y) = D(X) + D(Y)

• Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий:

D(X – Y) = D(X) + D(Y).

4.Дисперсия числа появлений события в независимых испытаниях.

Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:

D(X) = npq.

5.Среднее квадратическое отклонение Среднее квадратическое отклонение суммы взаимно независимых случайных величин.

Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии:

Сигма

Среднее квадратическое отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:

6.Одинаковое распределение взаимно независимых случайных величин.

Обозначим среднее арифметическое рассматриваемых случайных величин через :

.

Следующие ниже три положения устанавливают связь между числовыми характеристиками среднего арифметического и соответствующими характеристиками каждой отдельной величины.

1. Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию, а каждой из величин:

.

2. Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в n раз меньше дисперсии D каждой из величин:

3. Среднее квадратическое отклонение среднего арифметического n одинаково распределенных взаимно независимых случайных величин в 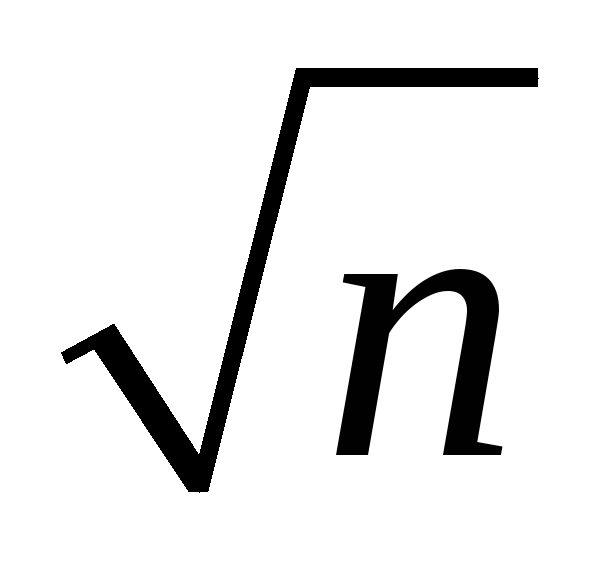раз меньше среднего квадратического отклонения, а каждой из величин:

7.Начальные и центральные теоретические моменты.

Определение. Начальным моментом порядка k случайной величины X называют математическое ожидание величины X^k:

v_k = M(X^k).

В частности,

v₁ = M(X), v₂ = M(X²).

Пользуясь этими моментами, формулу для вычисления дисперсии D(X) = М(X²) – [М(X)]² можно записать так:

. (7.5)

Кроме моментов случайной величины X целесообразно рассматривать моменты отклонения X – М(X).

Определение. Центральным моментом порядка k случайной величины X называют математическое ожидание величины (X – М(X))^k:

.

В частности,

. (7.6)

. (7.7)

Легко выводятся соотношения, связывающие начальные и центральные моменты. Например, сравнивая (7.5) и (7.7), получим