Нормальное распределение.

1.Числовые характеристики непрерывных случайных величин.

Определение. Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называют определенный интеграл

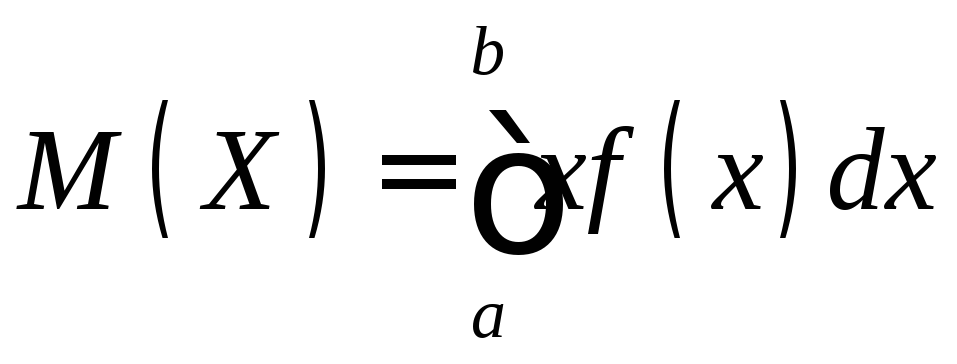. (11.1)

Если возможные значения принадлежат всей оси Ох, то

.

Предполагается, что несобственный интеграл сходится абсолютно, т.е. существует интеграл . Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к –, а верхнего – к +.

По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины.

Определение. Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения X принадлежат отрезку [а, b], то

;

если возможные значения принадлежат всей оси х, то

.

Определение. Среднее кеадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством

2.Нормальное распределение. Нормальная кривая.

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью

.

График плотности нормального распределения называют нормальной кривой (кривой Гаусса).

3.Вероятность попадания в заданный интервал нормальной случайной величины. Вычисление вероятности заданного отклонения. Правило 3х сигм.

в зад инт

Зад откл

3 сигм

Показательное распределение.

1.Определение показательного распределения. Вероятность попадания в заданный интервал показательно-распределительной случайной величины. Числовые характеристики показательного распределения.

Показательным или экспоненциальным называют распределение, которое характеризуется следующей функцией плотности: , где

Убедимся в том, что перед нами не «подделка». Поскольку и несобственный интеграл: , то функция действительно задаёт закон распределения НСВ

Таким образом, математическое ожидание показательного распределения равно величине, обратной параметру . Поэтому, если переменная x – время некоего процесса, то МХ=1/ имеет смысл времени релаксации (ослабления) этого процесса, когда плотность вероятности затухает в е раз. Тогда вероятность, что событие произойдет (например, лампочка перегорит) за время 1/, равна F(1/)–F(0)=1– 1/е=0.632.

Найдем дисперсию:

. (2.43)

Отсюда MX=(X)=1/.

Найдем вероятность попадания непрерывной случайной величины X, распределенной по показательному закону, на интервал (a;b). Воспользуемся общей формулой вероятности попадания непрерывной случайной величины X на заданный интервал:

P(a<X<b)=F(b)-F(a), где F(b)=1, аF(a)=1 Тогда имеем

P(a<X<b)=F(b) F(a)=1 (1)=

Буквы иные

2.Функция надёжности. Показательный закон надёжности.

пусть элемент начинает работать в момент времени t₀=0, а по истечении времени длительностью t происходит отказ. Обозначим через Т непрерывную случайную величину – длительность времени безотказной работы элемента. Если элемент проработал безотказно (до наступления отказа) время, меньшее t, то, следовательно, за время длительностью t наступит отказ.

Таким образом, функция распределения F(t) = P(T < t) определяет вероятность отказа за время длительностью t. Следовательно, вероятность безотказной работы за это же время длительностью t, т.е. вероятность противоположного события Т > t, равна

. (12.4)

Функцией надежности R(t) называют функцию, определяющую вероятность безотказной работы элемента за время длительностью t: .

Часто длительность времени безотказной работы элемента имеет показательное распределение, функция распределения которого . Следовательно, в силу соотношения (12.4) функция надежности в случае показательного распределения времени безотказной работы элемента имеет вид

.

Показательным законом надежности называют функцию надежности, определяемую равенством

. (12.5)

где  – интенсивность отказов.

Как следует из определения функции надежности, эта формула позволяет найти вероятность безотказной работы элемента на интервале времени длительностью t, если время безотказной работы имеет показательное распределение.