Векторная алгебра.

1.Декартова прямоугольная система координат. Полярная система координат. Связь декартовых и полярных координат.

Системы координат на плоскости.

Декартовы прямоугольные координаты (рис. 4.1). О - начало координат, Ох - ось абсцисс, Оy - ось ординат,- базисные векторы,- абсцисса точки M (- проекция точки M на ось Ох параллельно оси Оy),- ордината точки M (- проекция точки M на ось Oy параллельно оси Ox).

Системы координат в пространстве.

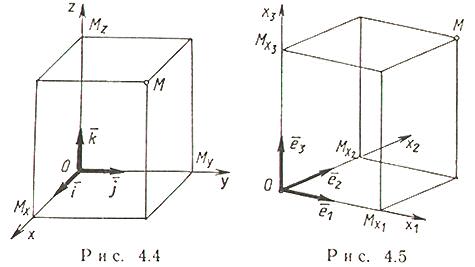
Декартовы прямоугольные координаты (рис. 4.4). О - начало координат, Ох - ось абсцисс, Оy - ось ординат, Оz - ось аппликат, - базисные векторы. Oxy, Oxz, Oyz - координатные плоскости,- абсцисса точки M (- проекция точки M на ось Ох параллельно плоскости Оyz),- ордината точки M (- проекция точки M на ось Oy параллельно плоскости Oxz),- ордината точки M (- проекция точки M на ось Oz параллельно плоскости Oxy).

Полярные координаты на плоскости. О - полюс, Ox - полярная ось, - полярный радиус,- полярный угол. Главные значенияи:(иногда).

Выражение декартовых прямоугольных координат через полярные:

Выражение полярных координат через декартовы прямоугольные:

2.Расстояние между двумя точками. Деление отрезка в данном отношении.

. В координатах:

на прямой ; на плоскости,; в пространстве,,.

3.Определение вектора. Линейные операции над векторами.

Вектором называется направленный отрезок (упорядоченная пара точек). К векторам относится также и нулевой вектор, начало и конец которого совпадают.

Ортом вектора а называется вектор а⁰, который имеет единичную длину и то же направление, что и вектор а.

Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.

Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.

Два вектора считаются равными, если они коллинеарные, одинаково направлены и равны по длине.

Линейными операциями над векторами называется сложение и умножение на число.

Суммой двух векторов a и b называется вектор c, направленный из начала вектора a в конец вектора b при условии, что начало b совпадет с концом вектора a. Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты.

Сумма любого конечного числа векторов может быть найдена по правилу многоугольника: чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего.

Разностью векторов a и b называют вектор a+(-b). Второе слагаемое является вектором, противоположным вектору b по направлению, но равным ему по длине.

4.Линейная зависимость и независимость векторов.

Векторы называются линейно зависимыми, если существует такая линейная комбинация , при не равных нулю одновременно a_i, т.е. . Если же только при a_i = 0 выполняется , то векторы называются линейно независимыми.

• Свойство 1. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы.

• Свойство 2. Если к системе линейно зависимых векторов добавить один или несколько векторов, то полученная система тоже будет линейно зависима.

• Свойство 3. Система векторов линейно зависима тогда и только тогда, когда один из векторов раскладывается в линейную комбинацию остальных векторов.

• Свойство 4. Любые 2 коллинеарных вектора линейно зависимы и, наоборот, любые 2 линейно зависимые векторы коллинеарны.

• Свойство 5. Любые 3 компланарных вектора линейно зависимы и, наоборот, любые 3 линейно зависимые векторы компланарны.

• Свойство 6. Любые 4 вектора линейно зависимы.

Условия коллинеарности, ортогональности и компланарности векторов.

Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.

Векторы называются ортогональными, если их скалярное произведение равно нулю.

Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными.

5.Понятие базиса. Координаты вектора в данном базисе.

1) Базисом в пространстве называются любые 3 некомпланарных вектора, взятые в определенном порядке.

2) Базисом на плоскости называются любые 2 неколлинеарные векторы, взятые в определенном порядке.

3) Базисом на прямой называется любой ненулевой вектор.

Три вектора, a,b,c, называются линейно-независимыми, если они не лежат в одной плоскости.

Базисом в трехмерном пространстве R³ называется упорядоченная тройка любых линейно-независимых векторов.

Упорядоченная тройка некомпланарных векторов e₁, e₂, e₃ называется базисом в множестве всех геометрических векторов. Всякий геометрический вектор a может быть единственным образом представлен в виде a=x₁e₁+x₂e₂+x₃e₃ числа x₁ , x_{2 ,} x₃ называют координатами вектора а в базисе (e₁, e₂, e₃).

6.Свойства, характерные для ортонормированного базиса. Направляющие косинусы и модуль вектора.

Векторы, расположенные на одной прямой или на параллельных прямых, называются коллинеарными.

Векторы называются ортогональными, если их скалярное произведение равно нулю.

Векторы, лежащие в одной плоскости или параллельные одной плоскости, называются компланарными

Определение. Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат.

Направляющие косинусы однозначно задают направление вектора.

Основное соотношение. Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора.

Соответственно, координаты единичного вектора равны его направляющим косинусам.

Свойство направляющих косинусов. Сумма квадратов направляющих косинусов равна единице.

7.Линейные операции над векторами в координатной форме.

Линейными операциями над векторами называется сложение и умножение на число.

Суммой двух векторов a и b называется вектор c, направленный из начала вектора a в конец вектора b при условии, что начало b совпадет с концом вектора a. Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты.

Сумма любого конечного числа векторов может быть найдена по правилу многоугольника: чтобы построить сумму конечного числа векторов, достаточно совместить начало каждого последующего вектора с концом предыдущего и построить вектор, соединяющий начало первого вектора с концом последнего.

Разностью векторов a и b называют вектор a+(-b). Второе слагаемое является вектором, противоположным вектору b по направлению, но равным ему по длине.

8.Основные теоремы о проекциях векторов.

Проекции векторов. Обозначения: - проекции векторана ось l;- величина проекции векторана ось l. Свойства проекций:

Составляющие (компоненты) вектора:

Координаты вектора :(- углы, образуемые вектором с положительными направлениями осей координат Ox, Oy, Oz прямоугольной декартовой системы координат).

, ,называются направляющими косинусами векторагдеЕсли- единичный вектор в направлении, то

9.Скалярное произведение векторов и его свойства. Угол между векторами.

Пусть даны два вектора. Параллельным переносом приведем их к общему началу. Наименьший угол, на который надо повернуть один вектор до совпадения с другим, называется углом между векторами.

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними, т.е. Из определения следуетгде φ - угол между векторами. Скалярная величинаназывается проекцией вектора на вектор .

В зависимости от значения угла между векторами, проекция может принимать отрицательные, положительные или нулевое значения.

Теперь можно написать . Из определения скалярного произведения следует, что если векторы ортогональны, то(условие ортогональности ненулевых векторов).

Свойства скалярного произведения.