МАТЕМЕТИКА

Матрицы. Решение систем линейных уравнений. Метод Гаусса.

1.Матрицы, виды матриц. Операции над матрицами: сложение, Умножение на число, Умножение матриц, транспонирование.

Матрицей называется прямоугольная таблица чисел, содержащая n строк и m столбцов.

Виды матриц:

• Две матрицы называются равными, если их соответствующие элементы равны.

• Если в матрице число строк равно числу столбцов (n=m), то матрица называется квадратной.

• Матрица, у которой все элементы, стоящие вне главной диагонали равны 0, называется диагональной.

• Диагональная матрица, у которой все диагональные элементы равны 1, называется единичной.

• Матрица, состоящая из одних нулей, называется нулевой.

• Если в квадратной матрице все элементы, стоящие ниже (выше) главной диагонали равны 0, то она называется верхний (нижний) треугольник.

• Если в матрице А строки записать столбцами с теми же номерами, то полученная матрица будет называться транспонированной к матрице А.

• Если матрица А равна транспонированной, то она называется симметричной.

Действия над матрицами:

• Умножение матрицы на число. В результате умножения матрицы на число получается матрица такой же размерности, что и исходная, каждый элемент которой является результатом произведения соответствующего элемента исходной матрицы на число. Мы получим одинаковый результат, умножая число на матрицу, или матрицу на число. Из определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.

• Сложение и вычитание матриц. Складывать и вычитать можно только матрицы одинаковой размерности. Суммой (разностью) двух матриц называется матрица той же размерности, что и исходные, каждый элемент которой определяется как сумма (разность) соответствующих элементов матриц. Очевидно, результат сложения не изменится, если слагаемые матрицы поменять местами. Если к матрице прибавить или от нее отнять нулевую матрицу той же размерности, то получим исходную матрицу.

• Умножение матрицы на матрицу. Умножать друг на друга можно только те матрицы, для которых число столбцов первого сомножителя равно числу строк второго сомножителя. Результатом умножения является матрица, у которой число строк равно числу строк первого сомножителя, а число столбцов совпадает с числом столбцов второго сомножителя. Иными словами, перемножать можно те матрицы, у которых совпадают средние индексы. Крайние индексы определяют размерность получаемого результата.

• Транспонирование матрицы-это операция над матрицей, когда ее строки становятся столбцами с теми же номерами.

2.Элементарные преобразования матриц. Ранг матрицы. Обратная матрица.

Элементарные преобразования матрицы — это такие преобразования матрицы, в результате которых сохраняется эквивалентность матриц, то есть, элементарные преобразования не изменяют множество решений системы линейных алгебраических уравнений, которую представляет эта матрица.

Элементарными преобразованиями строк называют:

• перестановку местами любых двух строк матрицы;

• умножение на ненулевую константу любой строки матрицы;

• прибавление к любой строке матрицы другой строки, умноженной на ненулевое число.

Аналогично определяются элементарные преобразования столбцов.

Рангом матрицы А (обозначается r(A)) называется наибольший порядок минора этой матрицы, отличного от нуля. Если все элементы матрицы равны нулю, то ранг такой матрицы принимают равным нулю.

Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы.

Ранг матрицы не изменится от следующих преобразований, называемых элементарными преобразованиями матрицы:

• замены строк столбцами, а столбцов соответствующими строками;

• перестановки строк матрицы;

• вычеркивания строки, все элементы которой равны нулю;

• умножения строки на число, отличное от нуля;

• прибавления к элементам строки соответствующих элементов другой строки, умноженной на одно и то же число.

Подчеркнем, что сама матрица при элементарных преобразованиях меняется, но ранг матрицы не изменится.

Обратная матрица. Матрицей, обратной матрице А, называется матрица A^-1 такая, что A^-1A = A A^-1 = E.

Обратная матрица может существовать только для квадратной матрицы. Причем сама является той же размерности, что и исходная матрица.

Можно показать, что для того, чтобы квадратная матрица имела обратную, она должна быть невырожденной (т.е. Δ ≠ 0 ). Это условие является и достаточным для существования A^-1 матрице А. Итак, всякая невырожденная матрица имеет обратную, и, притом, единственную.

Сформулируем правило нахождения обратной матрицы на примере матрицы А.

1. Находим определитель матрицы. Если Δ ≠ 0, то матрица A^-1 существует.

2. Составим матрицу В алгебраических дополнений элементов исходной матрицы А. Т.е. в матрице В элементом i - ой строки и j - го столбца будет алгебраическое дополнение A_ij элемента a_ij исходной матрицы.

3. Транспонируем матрицу В и получим B^T.

3.Системы уравнений. Матрица системы, расширенная матрица системы, расширение системы уравнений, совместимые и несовместимые системы.

Системы линейных уравнений. Уравнение называется линейным, если оно содержит неизвестные в первой степени и не содержит их произведений.

Запись в матричной форме.

- система линейных уравнений.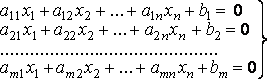

Обозначим, - матрица коэффициентов, - вектор неизвестных,

-вектор свободных членов. A_mn X_n1 + B_m1 = 0 - матричная запись системы уравнений.

Если система уравнений имеет решение, она называется совместной, не имеет – несовместной. Совместная система, имеющая одно решение, называется определенной, если много – неопределенной. Две системы уравнений называются равносильными или эквивалентными, если каждое решение является решением уравнения системы или наоборот.

РАСШИРЕННАЯ МАТРИЦА СИСТЕМЫ УРАВНЕНИЙ — матрица из коэффициентов системы линейных уравнений с неизвестными:

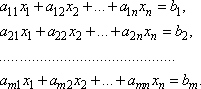
Р. м. с. у. получается добавлением к матрице системы столбца из свободных членов:

.

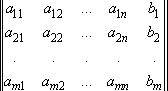Равенство рангов матрицы системы и Р. м. с. у. является необходимым и достаточным условием для совместности системы линейных уравнений. Это утверждение является содержанием Кронекера — Капелли теоремы.

Продолжаем разбираться с системами линейных уравнений. До сих пор я рассматривал системы, которые совместны и имеют единственное решение. Такие системы можно решить любым способом: методом подстановки («школьным»), по формулам Крамера, матричным методом, методом Гаусса. Однако на практике широко распространены еще два случая:

– Система несовместна (не имеет решений); – Система совместна и имеет бесконечно много решений.

Теорема Кронекера-Капелли. Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы. RgA = RgA*.

Исследование системы линейных уравнений.

4.Метод Гаусса: случай единственного решения и множества решений системы.

Решение и исследование систем линейных уравнений методом Гаусса. Этот метод решения систем линейных уравнений пригоден для решения систем с любым числом уравнений и неизвестных.

Суть метода Гаусса заключается в преобразовании заданной системы уравнений с помощью элементарных преобразований в эквивалентную систему ступенчатого треугольного вида.

Полученная система содержит все неизвестные в первом уравнении. Во втором уравнении отсутствует первое неизвестное, в третьем уравнении отсутствуют первое и второе неизвестные и т. д.

Если система совместна и определена (единственное решение), то последнее уравнение содержит одно неизвестное. Найдя последнее неизвестное, из предыдущего уравнения находим еще одно - предпоследнее. Подставляя полученные величины неизвестных, мы последовательно найдем решение системы.

Элементарными преобразованиями системы линейных уравнений, используемыми для приведения системы к треугольному виду, являются следующие преобразования:

- перестановка местами двух уравнений;

- умножение обеих частей одного из уравнений на любое число, отличное от нуля;

- прибавление к обеим частям одного уравнения соответствующих частей другого уравнения, умноженных на любое число.

Элементарные преобразования переводят данную систему линейных алгебраических уравнений в эквивалентную систему.

Две системы называются эквивалентными, если всякое решение первой системы является решением другой системы и наоборот.