
- •Курсова робота
- •Розділ 1 вибір промислового виду транспорту
- •Залежності для визначення витрат на перевезення
- •Витрати на перевезення різними видами транспорту
- •Розділ 2 визначення характеристик пасажирського транспорту міста
- •Результати розрахунку показників маршрутної мережі
- •Розділ 3 вибір транспортно-технологічної схеми доставки вантажів у магістральному сполученні
- •3.1 Пряме автомобільне сполучення
- •3.2 Автомобільно-залізничне сполучення
- •3.3 Автомобільно-водне сполучення
- •Висновки
- •Список використаної літератури
Розділ 2 визначення характеристик пасажирського транспорту міста
Забудована площа міста, км2
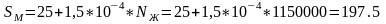
Середня довжина міського маршруту, км
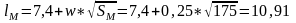
Мінімальна кількість маршрутів визначається з умови охоплення сполученням всіх транспортних мікрорайонів міста
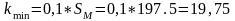
Максимальна кількість маршрутів визначається з умови забезпечення пасажирів всіх транспортних мікрорайонів сполученням без пересадок. З точністю достатньою для практичних розрахунків максимальна кількість маршрутів обчислюється залежністю:

Сумарна максимальна довжина маршрутів, км
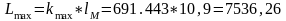
Мінімальна довжина маршрутної мережі, км

Сумарна довжина k маршрутів, км

Коефіцієнт пересадочності
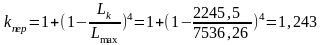
9) Щільність дорожньо-вуличної мережі, км/км2
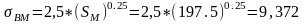
10) Маршрутний коефіцієнт
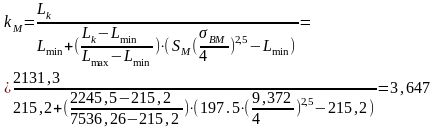
11) Щільність маршрутної мережі, км/км2

12) Середня відстань переміщення пасажира, км

13) Середня відстань поїздки пасажира, км
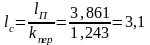
14) Витрати на підхід до зупинки, год

де Vn – швидкість пішохода (4 км/год)
lД – середня довжина перегону (0,7 км)
15) Розрахункова кількість рухомого складу

16) Витрати часу на очікування рухомого складу, год

17) Витрати часу на пересадку, год

18) Витрати часу на рух, год

де Vc – швидкість сполучення (Vc=1,2*Ve =1,2*18,4=22,08) км/год
19) Сумарні витрати часу на переміщення, год

Для
побудови залежностей приймаємо крок

Результати обчислень за формулами (2.7) – (2.19) заносимо в таблицю 2.1.
Таблиця 2.1
Результати розрахунку показників маршрутної мережі
L, км |
tn, год |
to, год |
tnp, год |
tp, год |
t, год |
206,1 |
0,289 |
0,013 |
0,012 |
0,278 |
0,593 |
672,1 |
0,232 |
0,044 |
0,029 |
0,242 |
0,547 |
1138,2 |
0,202 |
0,074 |
0,036 |
0,213 |
0,525 |
1604,2 |
0,183 |
0,104 |
0,036 |
0,191 |
0,514 |
2070,3 |
0,171 |
0,134 |
0,033 |
0,173 |
0,510 |
2536,3 |
0,161 |
0,164 |
0,027 |
0,159 |
0,511 |
3002,4 |
0,155 |
0,194 |
0,020 |
0,149 |
0,518 |
3468,4 |
0,149 |
0,225 |
0,014 |
0,141 |
0,528 |
3934,5 |
0,145 |
0,255 |
0,009 |
0,135 |
0,543 |
4400,6 |
0,141 |
0,285 |
0,005 |
0,130 |
0,561 |
На основі цих даних з таблиці 2.1 будуємо залежності tп = f(Lk), tо = f(Lk), tпр = f(Lk), tр = f(Lk), t = f(Lk), які зображаємо на рис.2.1.
Мінімальне
значення t за графіком t = f(Lk)
визначає оптимальну маршрутну мережу
загальною довжиною Lопт.
За допомогою залежностей (2.7)-(2.13)
визначаємо основні оптимальні
характеристики маршрутної мережі при
Lk=Lопт:
kпер=
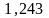 ;kM=
;kM=
 ;
; =
=
 ;l
;l =
=
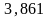 ;l
;l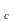 =3,1
=3,1

Рис. 2.1 Залежність витрат часу від довжини маршрутної мережі.
З рис. 2.1 видно, що мінімальне значення часу t = 0,510 год відповідає точці L = 2070,3 км. Це і є бажаний оптимум довжини маршрутної мережі.
20) Середня добова рухомість населення, поїздок:

21) Середня місткість рухомого складу, пас

де kH – коефіцієнт, що враховує нерівномірність пасажиро потоку у часі
(=2,5 - 2,8);
γ – середньодобовий коефіцієнт використання місткості рухомого складу
(=0,2 – 0,3)
ТН – час роботи транспорту на маршрутах міста (=18 год)
22) Математичне очікування середньої добової потужності пасажиро потоку на маршрутах, пас.км/км

Показавши, що А розподілено за нормальним законом і σ = А/3, визначаємо необхідний інтервал місткості рухомого складу.
Ця задача розв’язується графічним шляхом. Графік розподілу потужності пасажиропотоку f(A) поєднуємо з шкалою місткості рухомого складу так, як це показано на рис. 2.2, тобто точка середньої розрахункової місткості q (q=51 місць) сполучаємо (лінія Aq) із значенням середньої потужності пасажиропотоку А (А=4 пас.км/км). Потім знаходимо найближчу місткість автобуса – q1 , це автобус Богдан-А-095(місткість 68 пасажирів). Від точки q1 проводимо лінію q1A1 паралельно лінії Aq. Вона визначає А1, яке дорівнює 3,4 пас.км/км (див.рис.2.2). Величинам А1 і q1 приписуються перевезення з інтервалом Іс.
З умови пропорційності пасажирообігу інтервалу руху визначаємо:
 (2.25)
(2.25)
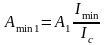 (2.26)
(2.26)
де Іmax = 15 хв;
Іmin =2 хв.
З (2.25) і (2.26) маємо:
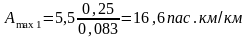

Будуємо інтервал Аmin1 – Amax1 .
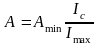 (2.27)
(2.27)
Звідси маємо:
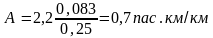 .
.
A` проекцюють на вісь q і знаходимо точку q́́́́`, яка становить 9 пасажиромісць. Найближча до цієї точки місткість рухомого складу – q2 визначає другу модель транспортного засобу. Це “ГАЗель”-32213 загальною пасажиромісткістю 12 місць. Проекцією точки q2 на вісь А одержуємо точку A2 (1.2). Підстановкою значення A2 замість A1 у формули (2.25) і (2.26) визначаємо кордони потужності пасажиропотоку (Аmin2–Amax2), який може бути засвоєний другою моделлю рухомого складу:
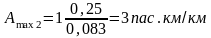
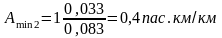
Будуємо інтервал Аmin2–Amax2. Перевіряємо, чи перекриває одержаний розрив рухомий склад з місткістю, середньою між визначеними крайніми. Для цього зони перекриття ділять вертикальними лініями ( В-В, рис.2.2 ) на дві частини. Місце проведення вертикальних ліній – це ½ інтервалу Аmin – Amax. Лінії розподілу зон перекриття визначають кордони використання рухомого складу різних марок.
Імовірність попадання випадкової величини в кожний із зазначених інтервалів :
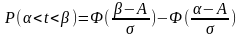 (2.28)
(2.28)
де Ф(~) – функція нормального закону розподілу, що визначається за таблицями;
α та β – нижній і верхній кордони інтервалу;
σ – параметр нормального закону, σ = А/3=4/3=1,33
Розглянемо два інтервали :
Рq2 (0<t<B(2,6))

Pq1 (2,6<t<6)
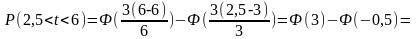
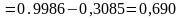
Перевірка Pq1 + Рq2 = 1, 0,307+0,690 = 0,997 ≈ 1.
Необхідна кількість рухомого складу:
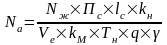 (2.31)
(2.31)
Кількість автобусів за моделями:
 (2.32)
(2.32)
де
P визначається за залежністю (2.29).
визначається за залежністю (2.29).
Таким чином, за формулою (2.31) розрахуємо необхідну кількість рухомого складу, а за формулою (2.32) кількість автобусів за моделями :
для автобуса місткістю q2 = 12 пас.:


для автобуса місткістю q1 = 68 пас.:
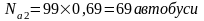
Отже, для міста необхідно 69 одиниць автобусів Богдан-А-095 загальною пасажиромісткістю 34 місць і 30 одиниць “ГАЗель”-32213 загальною пасажиромісткістю 12 місць.
