Свойство сравнимости в кольце многочленов над полем

Пусть P(x) – кольцо многочленов над полем Р

Опр.: a(x) = b(x) (mod f(x)) – сравнимы по модулю многочлена f(x), если остатки от деления совпадают:

a(x)=f(x)q₁(x)+r₁(x) и b(x)=f(x)q₂(x)+r₂(x) r₁=r₂

Утв.: Многочлены a(x)b(x) (mod f(x)) f(x)|a(x)-b(x)

Доказательство:

"" – очевидно из определения

"" – a(x)=f(x)q₁(x)+r₁(x) и b(x)=f(x)q₂(x)+r₂(x)

a(x)-b(x) = f(x)(q₁(x)-q₂(x)) + r₁(x)-r₂(x)

значит f(x)|r₁(x)-r₂(x), deg f(x)0, deg[r₁(x)-r₂(x)]<deg f(x)

следовательно r₁(x)-r₂(x)=0 ч.т.д.

Теорема: пусть f(x) – унитарный многочлен (далее везде). Для любого унитарного ненулевого многочлена f(x) – отношение сравнимости по (mod f(x)) – конгруэнция кольца.

Доказательство:

1. Покажем, что mod f(x) – отношение эквивалентности:

a(x)b(x)(mod f(x)) ~ f(x)|a(x)-b(x)

1. рефлексивность: f(x)|a(x)-a(x)

2. симметричность: f(x)|a(x)-b(x)

следовательно f(x)|b(x)-a(x), т.к. a(x)-b(x)=f(x)q(x)

значит b(x)-a(x)=f(x)(-q(x))

3. транзитивность: f(x)|a(x)-b(x), f(x)|b(x)-c(x) значит

a(x)-b(x)=f(x)q₁(x) + b(x)-c(x)=f(x)q₂(x)

a(x)-b(x)+b(x)-c(x)=a(x)-c(x)=f(x)(q₁(x)+q₂(x)). ч.т.д.

1. Покажем, что операции кольца многочленов согласованы с отношением mod f(x) – отношением эквивалентности:

2. множество многочленов кольца P[x]:

{a(x): a(x)b(x)(mod f(x))}=[b(x)]_f – класс эквивалентности для многочлена b(x);

2. берем два класса [a(x)], [b(x)] и по два многочлена a₁(x), a₂(x) и b₁(x), b₂(x), где a₁(x)a₂(x)(mod f(x)) и b₁(x)b₂(x)(mod f(x)).

Надо доказать, что

a₁(x)+ b₁(x) a₂(x)+ b₂(x)(mod f(x)) и a₁(x)^. b₁(x) a₂(x)^. b₂(x)(mod f(x)),

т.е. согласованность операций:

а) [a₁(x)-a₂(x)=f(x)^.q₁(x)] + [b₁(x)-b₂(x)=f(x)^.q₂(x)] значит

(a₁(x)+b₁(x))-(a₂(x)+b₂(x))= =f(x)(q₁(x)+q₂(x))

a₁(x)+b₁(x)a₂(x)+b₂(x) (mod f(x)) ч.т.д.

б) [a₁(x)=a₂(x)+f(x)q₁(x)][b₁(x)=b₂(x)+f(x)q₂(x)]

a₁(x)b₁(x)=a₂(x)b₂(x)+f(x)Q(x)

a₁(x)b₁(x)-a₂(x)b₂(x)=f(x)^.Q(x)

a₁(x)b₁(x)a₂(x)b₂(x) (mod f(x)) ч.т.д.

Следовательно это конгруэнция на кольце ч.т.д.

Следствие: Обозначим через – множество классов эквивалентности кольца многочленов P[x] относительно отношения эквивалентностити:

(mod f(x)). Определим на этих классах сложение и умножение: [a(x)]+[b(x)]=[a(x)+b(x)] и [a(x)]^.[b(x)]=[a(x)^.b(x)]

следовательно множество с введенными операциями – кольцо.

Доказательство:

1. Введенные операции определены корректно, т.е. результат не зависит от выбора элемента из класса:

a₁(x), a₂(x)[a(x)] значит [a(x)]=[a₁(x)]=[a₂(x)],

аналогично для b₁(x), b₂(x)[b(x)]. По теореме о конгруэнции [a₁(x)+b₁(x)]=[a₂(x)+b₂(x)], а [a₁(x)+b₁(x)]=[a₁(x)]+[b₁(x)] следовательно [a₁(x)]+[b₁(x)]=[a₂(x)]+[b₂(x)].

Аналогично для умножения. ч.т.д.

2. Выполнение аксиом кольца для многочлена (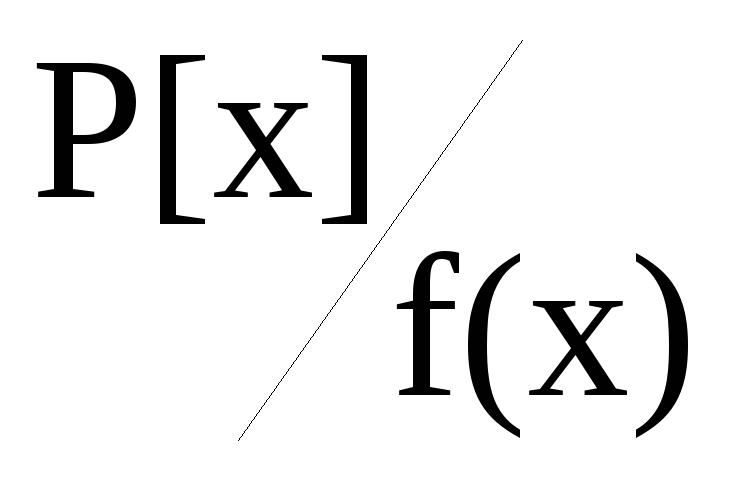,+,×) вытекает из их справедливости в кольце многочленов P[x].

Из [a(x)] выберем представителя и будем работать с ним, отождествляя результат со всем классом.

Опр.: Множество многочленов a₁(x), a₂(x),…,a_t(x) – полная система представителей классов эквивалентностити относительно отношения º(mod f(x)) если:

1. для любого j¹k a_j(x) не сравним с a_k(x)(mod f(x))

2. для люього b(x)P[x] существует k : b(x)=a_k(x) (mod f(x)).

Утв.: Пусть f(x)=xⁿ+_jx^j, т.е. унитарный многочлен степени n. Множество многочленов вида {_jx^j, c_jP, j=} – ПСПºf(x) – полная система представителей для данного отношения эквивалентности.

Утв.: Пусть |P|=q<+.

=qⁿ.

Доказательство: каждый класс однозначно определяется своими представителями вида _jx^j, а т.к. c_jP, то каждый класс сможем выбрать q способами, следовательно всего классов qⁿ.

Теорема: Многочлен a(x) – обратим в кольце (a(x),f(x))=1 (Под обратимостью многочлена a(x) понимаем, что существует

[b(x)] : [a(x)]^.[b(x)]=[e])

Доказательство:

"" Существуют u(х), v(х) : a(x)u(x)+f(x)v(x)=1

Разделим на f(x) и возьмем остатки от деления:

res_f(x)(a(x)^.u(x))=1, следовательно a(x)^.u(x)1 (mod f(x)), таким образом a(x) – обратим;

"" от противного:

a(x)=_jx^j. ] (a(x),f(x))=d(x), deg <deg f(x);

a(x)^. =f(x)=0 (mod f(x)).

и a(x) неэквивалентны 0 (mod f(x)), значит a(x) – делитель нуля, следовательно он необратимый элемент кольца (по теореме) – противоречие. ч.т.д.

Следствие: Множество - поле когда многочлен f(x) – неприводим.

Доказательство: переходим к представлению _jx^j, deg f(x)=n

"" Если f(x) – неприводим, то многочлен f(x) взаимопрост с любым ненулевым многочленом меньшей степени, следовательно по доказанной теореме c(x) – обратим:

(c(x),f(x))=1 и _jx^j0, т.е. любой ненулевой элемент обратим,

следовательно - поле. ч.т.д.

"" Если f(x) – приводим, т.е. f(x)=f₁(x)^.f₂(x), где 0<deg f₁(x)<deg f₂(x)<deg f(x) значит f₁(x)^.f₂(x)=0 (mod f(x)) , т.е. f₁(x) – делитель нуля, следовательно - не поле – противоречие. ч.т.д.