
- •Опр.: в конечном поле элемент с таким свойством называется примитивным т.Е. В конечном поле существует примитивный элемент, где 0, 1, 2, …,|p|-1 – все различные элементы поля р
- •Кольцо многочленов над полем
- •Алгоритм Евклида
- •Свойства взааимнопростых многочленов
- •Свойства неприводимых многочленов
- •Свойство сравнимости в кольце многочленов над полем
- •Корни многочленов над конечным полем и их свойства
- •Неприводимые многочлены над числовым полем с, полем действительных чисел r и полем рациональных чисел z
2)
– противоречит тому, что Р – поле,
следовательно наше предположение о
том, что Р=n1![]() n2
– ошибочно, значит Р – простое число.
n2
– ошибочно, значит Р – простое число.
Опр.:
Пусть Р – поле следовательно множество
Q![]() P – подполе
Р,
если Q
P – подполе
Р,
если Q![]() P и Q – поле.
P и Q – поле.
Пример: Q < R < C
Опр.:
Поле называется простым, если оно не
содержит собственных подполей, т.е. если
Q<P значит Q=P![]() (более
простых полей, чем Р в нем нет).
(более
простых полей, чем Р в нем нет).
Теорема: В каждом поле существует, причем единственное, простое подполе.
Доказательство:
1)
Пусть char P=0, e![]() P
P
Пусть
Q<P. Тогда
рассмотрим множество Q*=Q\0 – множество
ненулевых элементов подполя Q – это
мультипликативная группа, а Q*![]() P*.
Тогда Q*<P*, а е – подгруппа Q* совпадает
с е в Р*, т.к. ab-1
P*.
Тогда Q*<P*, а е – подгруппа Q* совпадает
с е в Р*, т.к. ab-1![]() Q*;
пусть a
Q*;
пусть a![]() Q*,
b=a и е=аа-1
Q*,
b=a и е=аа-1![]() Q*,
т.е. е
Q*,
т.е. е![]() Q*
- единица принадлежит подполю
Q*
- единица принадлежит подполю
![]() Qэ{0,e}, а т.к. Qэe , то 2e, 3e, …
Qэ{0,e}, а т.к. Qэe , то 2e, 3e, …
![]() Q
– в силу замкнутости по сложению.
Q
– в силу замкнутости по сложению.![]()
![]() а т.к. (Q,+) – группа, то -е, -2е, -3е, …
а т.к. (Q,+) – группа, то -е, -2е, -3е, …
![]() Q
Q
![]()
![]() n
n![]()
![]() \0,
(ne)-1
\0,
(ne)-1![]() Q
– существование обратного по умножению
Q
– существование обратного по умножению
![]()
![]() m
m![]()
![]() ,
n
,
n![]()
![]() \0,
(me)(ne)-1=
\0,
(me)(ne)-1=![]() e
e![]() Q
– в силу замкнутости по умножению
Q
– в силу замкнутости по умножению
Вывод:
если char P=0, то {![]() e
e![]() Q
Q![]() P,
m
P,
m![]()
![]() ,
n
,
n![]()
![]() \0}=P0,
т.е. если Q – подполе, то P0
\0}=P0,
т.е. если Q – подполе, то P0![]() Q,
для
Q,
для
![]() Q<P.
Q<P.
Теперь покажем, что Р0 – поле:


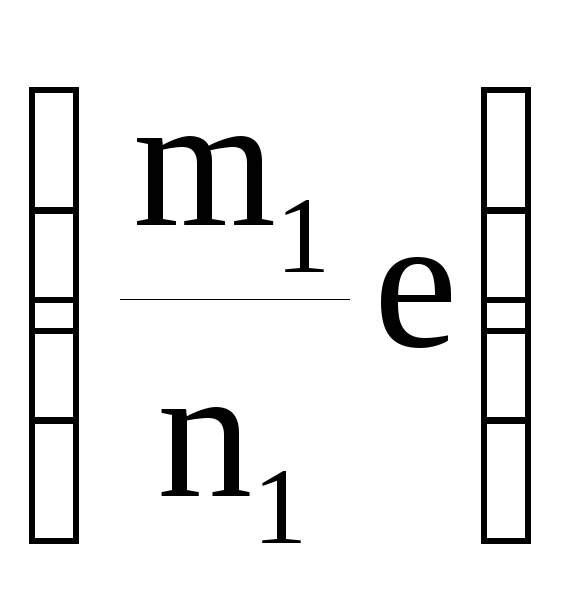 =
=
 операции сложения и умножения замкнуты
операции сложения и умножения замкнутыассоциативность, коммутативность следуют из ассоциативности, коммутативности Р
дистрибутивность
обратное по сложению
обратное по умножению
![]() Р0
– поле.
Р0
– поле.
Покажем, что Р0 – простое поле: Пусть существует Q'<P0, а по доказанному P0<Q' следовательно Q'=P0 ч.т.д.
Замечание:
из доказательства следует, что простое
подполе поля с характеристикой равной
нулю изоморфно полю рациональных чисел,
т.к. {![]()
![]() Q
Q![]() P,
m
P,
m![]()
![]() ,
n
,
n![]()
![]() \0}=P0
(е – опускаем).
\0}=P0
(е – опускаем).
2) Пусть char P=Р
а)
т.к. Q<P значит
e![]() Q
(было доказано выше), следовательно
е,2е,…,(р-1)е, ре=0, следовательно {0, e, 2e, …,
(p-1)e}=P0
Q
(было доказано выше), следовательно
е,2е,…,(р-1)е, ре=0, следовательно {0, e, 2e, …,
(p-1)e}=P0
Рассмотрим
Zp:
пусть
![]() :
P0
:
P0![]() Zp
Zp
![]() (a,e)=[a]p
– взаимно однозначное отображение
(a,e)=[a]p
– взаимно однозначное отображение
![]() (ae
(ae![]() be)=
be)=![]() (ae)
(ae)![]()
![]() (be), где
(be), где
![]()
![]()
следовательно
P0![]() Zp
(т.е. изоморфны), значит т.к. Р0
- поле, т.к. Zp
– поле.
Zp
(т.е. изоморфны), значит т.к. Р0
- поле, т.к. Zp
– поле.
б)
Р0
– простое, т.к. Q'![]() P0
и P0
P0
и P0![]() Q'
следовательно Q'=P0
ч.т.д.
Q'
следовательно Q'=P0
ч.т.д.
Теорема:
Пусть P – конечное поле, тогда существует
![]() Р
: ord
Р
: ord![]() =
=![]() -1;
(ord
-1;
(ord![]() - по умножению в мультипликативной
группе Р*).
- по умножению в мультипликативной
группе Р*).
Опр.: в конечном поле элемент с таким свойством называется примитивным т.Е. В конечном поле существует примитивный элемент, где 0, 1, 2, …,|p|-1 – все различные элементы поля р
{В
абелевой группе существует
![]() : ord
: ord![]() =expG}
=expG}
expG=min{t :
![]()
![]()
![]() G,
G,
![]() t=e}
t=e}
1) expP*=|P|-1
expP*/|P*|=|P|-1
Пусть
expP*<|P|-1 следовательно XexpP*-1=0
– это уравнение имеет в поле Р
(|P|-1)-решений, т.е.
![]() ненулевой элемент в поле – решение.
ненулевой элемент в поле – решение.
![]() противоречие: решений > степени
уравнения (что противоречит теореме
Безу)
противоречие: решений > степени
уравнения (что противоречит теореме
Безу)
![]() expP*<|P|-1
expP*<|P|-1
2)
P* - абелева группа, значит существует
![]() : ord
: ord![]() =expP*
=expP*
Из 1) и 2) следует утверждение теоремы.
Кольцо многочленов над полем
Пусть Р – поле;
Обозначим:
Р![]() - множество носителей с элементами из
Р; (а0
а1
а2
… ), аj
- множество носителей с элементами из
Р; (а0
а1
а2
… ), аj![]() Р
Р
![]()
![]() Р
Р![]() : если (а0
… аn
…)
: если (а0
… аn
…)![]()
![]() ,
то
,
то
![]() k
: аj=0,
для j
k
: аj=0,
для j![]() k,
т.е. начиная с какого-то номера они все
нули.
k,
т.е. начиная с какого-то номера они все
нули.
Определим
на множестве
![]() :
:
![]() +
+![]() =
=![]() ,
ck=ak+bk
,
ck=ak+bk
![]() ×
×![]() =
=![]() ,
ck=
,
ck=![]() ajbk-j
ajbk-j
Теорема:
(![]() ,+,×)
– коммутативное кольцо.
,+,×)
– коммутативное кольцо.
Доказательство: "по сложению":
1)
![]() +
+![]()
![]()
![]() ,
т. к. начиная с max(k, n) – все нули.
,
т. к. начиная с max(k, n) – все нули.
![]()
![]()
![]()
![]()
2) эта операция коммутативна
3)
![]() =(0,
0, …)
=(0,
0, …)
4)
-![]() =(
-а0
,-а1,
…)
=(
-а0
,-а1,
…)
"по
умножению": 1) замкнутость
![]() ×
×![]() =
=![]() max{j, aj
max{j, aj![]() 0}=k,
max{j, bj
0}=k,
max{j, bj![]() 0}=n,
тогда cn+k+1=
0}=n,
тогда cn+k+1=![]() ajbn+k-j+1=0
ajbn+k-j+1=0

 0,0,….,0
0,0,….,0
a0, a1, …, ak, ….…, an+k+1
![]()
![]()
![]() -
сумма индексов в столбце всегда (n+k+1)
-
сумма индексов в столбце всегда (n+k+1)
bn+k+1,…, bn+1,…..,b1,b0
 0,0,……,0
0,0,……,0
![]() каждое
произведение равно 0
каждое
произведение равно 0
![]() при
таком определении умножения мы из
множества
при
таком определении умножения мы из
множества
![]() не выходим.
не выходим.
2) коммутативность:
ck=![]() ajbk-j=
ajbk-j=![]() bk-jaj=
bk-jaj=![]() bj'ak-j'=dk,
где
bj'ak-j'=dk,
где
![]() =(
=(![]() ×
×![]() ),
),
![]() =(
=(![]() ×
×![]() )
)
3)
ассоциативность: пусть (![]() ×
×![]() )=
)=![]() ,
(
,
(![]() ×
×![]() )=
)=![]() и (
и (![]() ×
×![]() )
)![]() =
=![]() ,
,
![]() (
(![]() ×
×![]() )=
)=![]() ,
,
тогда
dk=![]() (vjck-j)=
(vjck-j)=![]()
![]() asbj-sck-j
asbj-sck-j
fk=![]() aswk-s=
aswk-s=![]()
![]() asbjck-j=
asbjck-j=
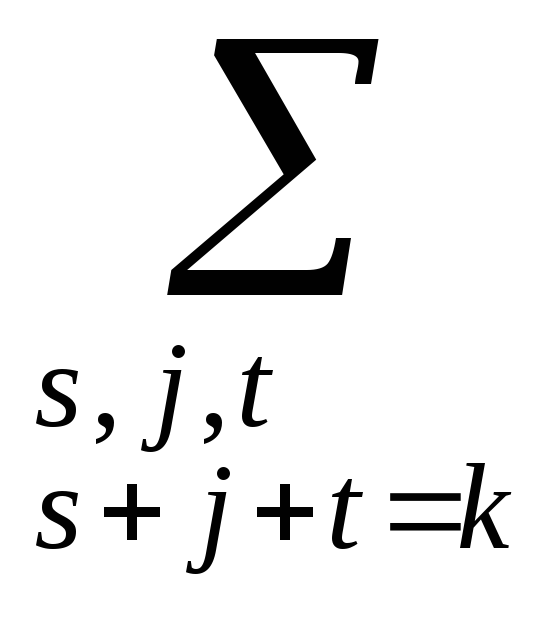 asbjct
asbjct
(![]() +
+![]() )
)![]() =
=![]()
![]() +
+![]()
![]() ч.т.д.
ч.т.д.
![]() вот
это кольцо - кольцо многочленов над
полем
вот
это кольцо - кольцо многочленов над
полем
![]()
Введем
обозначения:
![]() ×
(
×
(![]() )=(0,а0,а1,а2,
…) – такое умножение {ck=
)=(0,а0,а1,а2,
…) – такое умножение {ck=![]() ajbk-j=ak-1
при k-j=1
ajbk-j=ak-1
при k-j=1![]() j=k-1}
есть сдвиг последовательности вправо
а(0,1,0,…,0)=(0,а,0,…,0);
j=k-1}
есть сдвиг последовательности вправо
а(0,1,0,…,0)=(0,а,0,…,0);
![]() =
=![]() (0,…,аj,0,…)=
(0,…,аj,0,…)=
![]() аj(0,…,1,0,…)=
аj(0,…,1,0,…)=
![]() аj(0,1,0…)j={
]x=(0,1,0,...)}=
аj(0,1,0…)j={
]x=(0,1,0,...)}=
![]() аjxj
аjxj
Опр.: Будем говорить, что многочлен a(x) делит b(x), т.е. a(x)½b(x), если существует с(х) : a(x)× c(x)=b(x)
Опр.:
Степень
многочлена a(x)
– deg a(x) – номер наибольшего ненулевого
коэффициента в представлении: a(x)=![]() ajxj.
ajxj.
Если
а(х)=0, то полагаем deg a(x)= -![]()
(примечание:
пусть a(x)=a0![]() 0
тогда deg a(x)=0).
0
тогда deg a(x)=0).
Опр.: Разделить a(x) на b(x) с остатком – значит, что b(x) можно представить в виде b(x)=q(x)a(x)+r(x), deg r(x)<deg a(x)
Утв.:
Если а(х)![]() 0,
то любой многочлен над полем можно
разделить с остатком на а(х) и представление
b(x)=q(x)a(x)+r(x), deg r(x)<deg a(x) определено
однозначно.
0,
то любой многочлен над полем можно
разделить с остатком на а(х) и представление
b(x)=q(x)a(x)+r(x), deg r(x)<deg a(x) определено
однозначно.
Доказательство:
a(x)![]() 0
следовательно deg a(x)
0
следовательно deg a(x)![]() 0
0
a(x)=anxn+an-1xn-1+…+a0
(an![]() 0)
0)
b(x)=bmxm+bm-1xm-1+…+b0
m<n следовательно b(x)=0.a(x)+b(x)
m
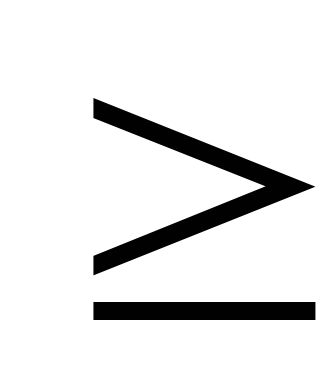 n следовательно
b(x)-a(x).an-1bmxm-n=bm-1(1)xm-1+…+b0(1)=b(1)(x)
n следовательно
b(x)-a(x).an-1bmxm-n=bm-1(1)xm-1+…+b0(1)=b(1)(x)
{т.е. степень понизили как минимум на 1}
Если deg b(n)(x)<n, то STOP иначе понижаем степень дальше также;
b(x)-a(x)an-1bmxm-n-a(x)an-1bdeg b(')(x)(1)xdeg b(')(x)-n=r(x); deg r(x)<n
(за конечное число шагов такое неравенство обязательно получим)
значит b(x)-a(x)q(x)=r(x)
Однозначность деления: -доказательство от противного-
пусть существует: b(x)=a(x)q'(x)+r'(x) deg r'(x)<deg a(x)
b(x)=a(x)q(x)+r(x) deg r(x)<deg a(x)
Вычитаем: 0=a(x)(q'(x)-q(x))+r'(x)-r(x) следовательно
r(x)-r'(x)=a(x)(q'(x)-q(x))
deg (r(x)-r'(x))<deg a(x)
deg
a(x)(q'(x)-q(x))=deg a(x)+deg (q'(x)-q(x))![]() deg
a(x)
deg
a(x)
возникает противоречие, т.е. q'(x)-q(x)=0 следовательно q'(x)=q(x) ч.т.д.
(ab)c=a(bc); пусть (ab)=u, (bc)=v, тогда
![]() ak-jvj=
ak-jvj=![]() asbj-s)ck-j=
asbj-s)ck-j=![]() asbj-sck-j=
asbj-sck-j=![]() asbj-sck-j={замена
t=k-j
asbj-sck-j={замена
t=k-j
![]() j=k-t}= =
j=k-t}= =![]() asbk-t-sct={замена
l=k-s
asbk-t-sct={замена
l=k-s
![]() s=k-l}=
s=k-l}=![]() ak-lbl-tct
ak-lbl-tct
![]()
![]() ujck-j=
ujck-j=![]() ak-jvj.
ak-jvj.
