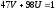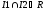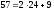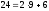Лекции / Лекции Кузьмина / ALG#04
.DOC
Утв:
Пусть
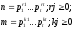
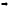
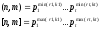
Кольцо вычетов целых чисел.
 -
конгруэнция на Z.
Пусть [a]n
– класс
эквивалентных элементов относительно
-
конгруэнция на Z.
Пусть [a]n
– класс
эквивалентных элементов относительно
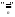 ;
;
 а остатков:
а остатков:
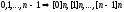 - разные классы.
- разные классы.
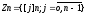 -
множество + операции:
-
множество + операции:
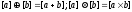 .
В
силу теоремы, что
.
В
силу теоремы, что
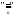 - конгруэнция, введенные операции –
введены корректно.
- конгруэнция, введенные операции –
введены корректно.
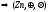 - это множество с этими операциями –
это кольцо из n
элементов.
- это множество с этими операциями –
это кольцо из n
элементов.
Для
простоты:
 - наименьший неотрицательный элемент
из класса [a]
- наименьший неотрицательный элемент
из класса [a]
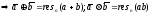 .
.
Идеалы колец.
Опр:
Пусть
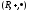 - кольцо
- кольцо
 - идеал кольца R,
если
- идеал кольца R,
если
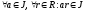 .
.
Пример:
R=Z,
J –
четные числа
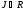 .
.
Рассматриваем свойства коммутативных колец.
Опр:
Идеал I
–
максимальный идеал, если из условия,
что
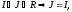 либо J=R.
либо J=R.
Утв:
Если есть 2 идеала:
 то:
то:
Док-во:
-
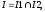 если
если
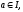 то
то
 для
для
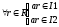
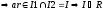
-
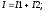 Пусть
Пусть
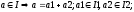
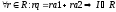
Опр:
Пусть
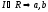 - сравнение по модулю идеала I:
- сравнение по модулю идеала I:
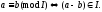
Теорема:
Пусть R-
коммутативное кольцо:
 :
:
-
Отношение сравнимости
 - конгруэнция кольца.
- конгруэнция кольца. -
Если I – max, то кольцо
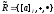 - поле.
- поле.
Док-во: это отношение эквивалентности, т.к.:
-
Рефлективное:
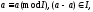 т.е.
т.е.
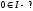 Пусть
Пусть

-
Симметричное:

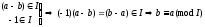
-
Транзитивное:
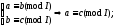
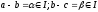 ;
;
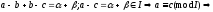 это
отношение эквивалентности, значит
разбивает кольцо на не пересекающиеся
классы:
это
отношение эквивалентности, значит
разбивает кольцо на не пересекающиеся
классы:
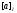
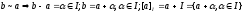
Определим операции на классах:
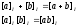
Док-во корректности введенных операций:
-
[a]+[b]=a+I+b+I=(a+b)+(I+I)=(a+b)+I=[a+b]
-
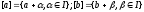

Отношение
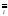 - конгруэнция
на R;
значит
получается, что
- конгруэнция
на R;
значит
получается, что
 - кольцо.
- кольцо.
Идеалы кольца целых чисел.
Теорема:
Все идеалы кольца целых чисел исчерпываются
множествами вида:
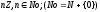 .
.
Док-во:
что
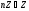
-
что nZ<Z, т.е. под кольцо
-
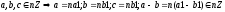 ,
т.е.
(nZ,+)
– кососимметричная группа.
,
т.е.
(nZ,+)
– кососимметричная группа. -
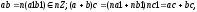 т.е.
дистрибутивность для данных чисел
выполняется в силу того, что она
выполняется для всех целых чисел.
т.е.
дистрибутивность для данных чисел
выполняется в силу того, что она
выполняется для всех целых чисел.
-
-
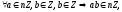 т.к.
т.к.
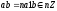
-
Покажем, что любой идеал имеет такой вид, т.е. если
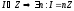
-
Если I={0}, то n=0, I=0*Z
-
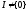 ,
т.е.
состоит не из одного нуля.
,
т.е.
состоит не из одного нуля.
 если и I
есть элементы не равные нулю, то там
есть положительные элементы, отличные
от нуля. Возьмем наименьшее такое
число:
если и I
есть элементы не равные нулю, то там
есть положительные элементы, отличные
от нуля. Возьмем наименьшее такое
число:
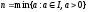 .
Введем:
.
Введем:
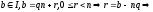
 но
но
 .
.
-
Теорема:
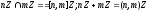 .
.
Док-во:
-
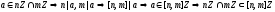 .
Возьмем:
.
Возьмем:

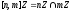
-
Аналогично:
 если
если
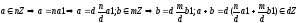 ,
т.е.
,
т.е.
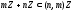 .
Обратно:
.
Обратно:

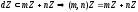 .
.
Следствие:
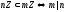 .
.
Теорема: Идеал nZ – max n – простое число.
Док-во:
(от противного) Прямое: Пусть
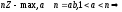
 - противоречит с тем, что nZ
– max => n – простое.
- противоречит с тем, что nZ
– max => n – простое.
Обратное:
n
– простое;
Пусть
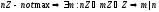 ,
а
т.к.
,
а
т.к.
 - противоречит тому, что n
– простое.
- противоречит тому, что n
– простое.
Теорема:
Кольцо вычетов Zm
– поле
m – простое
число.
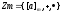 .
.
Док-во:
нужно проверить, что каждый элемент
является обратным, значит пусть Zm
– поле,
но m
– составное,
т.е.
 т.е.
[a]
и
[b]
–
делители нуля, а в поле их нет.
т.е.
[a]
и
[b]
–
делители нуля, а в поле их нет.
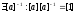 - по свойству поля.
- по свойству поля.
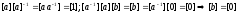 ,
но
,
но
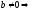 если
Zm
– поле, то m
– не может быть составным.
если
Zm
– поле, то m
– не может быть составным.
Обратно:
Пусть m
– простое.
Возьмем
 ,
но
,
но
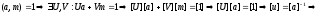 любой
элемент имеет обратный, значит Zm
–
поле.
любой
элемент имеет обратный, значит Zm
–
поле.
СМ.ПР
Решение сравнения в кольце целых чисел Zn.
Пусть
 - обозначение. Дано: Zn;
[a][x]=[b];
- обозначение. Дано: Zn;
[a][x]=[b];
 ;
Пусть
;
Пусть
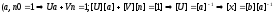
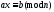 -
сравнение по модулю n,
здесь
решений бесконечное множество т.к. в
Zn.
-
сравнение по модулю n,
здесь
решений бесконечное множество т.к. в
Zn.
Теорема:
-
В Zn сравнение:
 имеет
решение (a,n)|b
имеет
решение (a,n)|b -
Если (a,n)|b, то сравнение имеет (a,n)=d различных по модулю n решений вида:
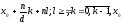 - некоторое фиксированное решение.
- некоторое фиксированное решение.
Док-во:
-
-
Прямое: Пусть есть решение
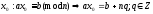 ;
;
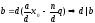
-
Обратное: Пусть
 где
где
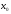 - решение 1-го сравнения
- решение 1-го сравнения
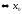 - решение 2-го сравнения. Покажем это:
Пусть
- решение 2-го сравнения. Покажем это:
Пусть
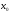 -
решение 1-го сравнения
-
решение 1-го сравнения
 ,
т.е.
эти равенства эквивалентны.
,
т.е.
эти равенства эквивалентны.
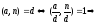 .
Пусть
.
Пусть
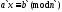 ,
где
,
где
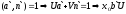 -
решение этого сравнения, т.к.
-
решение этого сравнения, т.к.
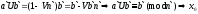 - это решение и исходного сравнения.
- это решение и исходного сравнения.
-
-
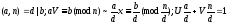 ,
то
,
то
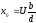 - решение. Пусть есть еще решение:
- решение. Пусть есть еще решение:
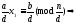
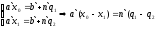 ,
а
т.к.
,
а
т.к.
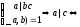
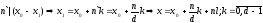 ,
т.е.
при фиксированном l
получаем
d
различных решений.
,
т.е.
при фиксированном l
получаем
d
различных решений.
Пример1:
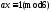
-
(a,6)=1 Пусть a=5;
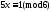
-
5U+6V=1; U=-1
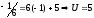
-
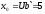
-
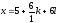
Пример2:
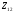 .
Найти
обратный к элементу [4]?
.
Найти
обратный к элементу [4]?
 нет
решений. Пусть
нет
решений. Пусть
 есть решение.
есть решение.
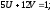 Пусть
Пусть
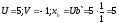
Пример3: Сумма пересечений идеалов:
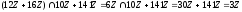
Пример4:

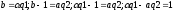
Пример5: 57, 24. Алгоритм Евклида:
U0=0
U1=-2
U2=U0-q2U1=0-2=-2
U3=U1-q3U2=-2-5=-7
V0=1
V1=-2
V2=V0-q2V1=1-2(-2)=5
V3=V1-q3V2=-2-5=-7
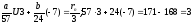
Пример6: 8,10,15 – их NOD в виде их линейной комбинации.
(6,10)=2; (2,15)=1 => (6,10,15)=1
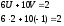 или
или
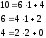
U0=0
U1=1
U2=U0-q2U1=-1
V0=1
V1=-q1=-1
V2=V0-q2V1=1-1(-1)=2
2=(-1)10+2*6
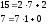
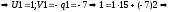
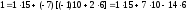
Пример8:
Кольцо
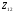 .
.
Обратимые: Необратимые:

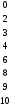
Найти
обратные: ab=1;
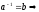 тоже
обратим
тоже
обратим
Обратные образуют мультипликативную группу:
-
Замкнутость: a,b – обратимы

-
Ассоциативность выполняется для любых элементов в кольце.
-
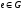 и
если а обратим
и
если а обратим
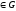 ,
то
,
то
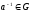 ,
т.к.
,
т.к.
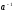 - обратим.
G={1,5,7,11}
- обратим.
G={1,5,7,11}
Пример9:
Кольцо

47
– обратим. Построим обратный к 47 по
умножению:
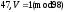
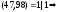 есть
решение.
есть
решение.