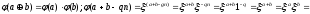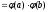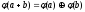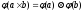Лекции / Лекции Кузьмина / ALG#01
.DOCЭлементы теории множеств.
Бинарное
отношение
на множестве Х – любое подмножество
декартового квадрата множества Х.
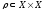 .
.
Декартово
произведение множеств:
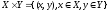 ,
для n
множеств
,
для n
множеств
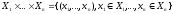 .
.
Если
 то
~
то
~
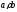 .
.
Свойства бинарного отношения:
-
Рефлексивность:
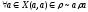
-
Симметричность:
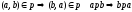
-
Транзитивность:
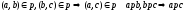
-
Ассимитричность:
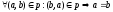
Отношение эквивалентности: если оно рефлексивно, симметрично, транзитивно.
Отношение порядка: если оно рефлексивно, транзитивно, ассимитрично.
(Строгого порядка – если 3.)
Пример 1: отношение равенства – отношение эквивалентности.
Пример
2:
Множество действительных чисел с
оператором
 - отношение порядка.
- отношение порядка.
Пример 3: R с < - выполняется только 3.
Пример 4: Выполняется 3, 4 и не выполняется 1, 2.
X={1,2,3}; p={(1,2),(2,3),(1,3)}
4 выполняется автоматически, так как нет пар (a,b),(b,a).
Теорема 1:
Опр:
Пусть р – отношение эквивалентности
на Х, тогда множество элементов
 - класс эквивалентных элементов для
элемента а по отношению р.
- класс эквивалентных элементов для
элемента а по отношению р.
-
Пусть р – отношение эквивалентности на Х, тогда множество Х представляется в виде пересечения попарно не пересекающихся классов эквивалентности.
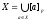
-
Любое разбиение множества Х на не пересекающиеся подмножества задает отношение эквивалентности на Х.
Доказательство: Докажем, что если два класса эквивалентности пересекаются, то они совпадают. Этого будет достаточно.
От
противного: Пусть
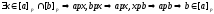
В
другую сторону: Пусть

Определим отношение эквивалентности:
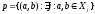 -
покажем, что это отношение эквивалентности:
-
покажем, что это отношение эквивалентности:
-
 -
рефлексивное
-
рефлексивное -
Пусть
 - симметричное
- симметричное -
Транзитивность: Пусть
 т.к.
по условию все
т.к.
по условию все
 не пересекаются попарно.
не пересекаются попарно.
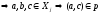
Будем
говорить, что а делится на в с остатком,
если
 .
.
Будем говорить, что a, b – сравнимы по mod n, если остатки от деления a, b на n совпадают:
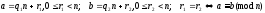
Отношение сравнимости по любому mod n на множестве Z – отношение эквивалентности.
Основные алгебраические структуры.
Опр:
Отображение множества Х в множество Y
– закон по которому каждому
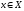 ставится в соответствие некоторый
ставится в соответствие некоторый
 .
.
Заметим,
что бинарное отношение
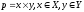 .
.
Свойства отображений:
-
Сюръективность.
-
Инъективность.
-
Биективность.
Опр:
Бинарная операция на множестве Х –
отображение декартового квадрата
множества Х в себя:

Свойства операций:
-
Коммутативность (обозначим +):
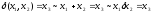 ,
если
,
если
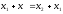 .
. -
Ассоциативность (*):

-
Дистрибутивность (*,0):

Опр: Множество Х с бинарной операцией * - полугруппа (Хб*)
-
Пример (N,
 )
)
Опр:
Пусть (Х,*) – полугруппа, элемент
е-еденичный, если
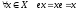
Опр:
Для
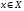 элемент
элемент
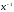 - обратный, если
- обратный, если
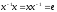
Опр:
Полугруппа (Х,*) – группа, если существует
е относительно * и для каждого

Пример: (Z,+)
Опр: Пусть на множестве Х введены две операции: (Х,+,0) – множество Х с двумя бинарными операциями – кольцо, если:
-
(Х,+) – абелева группа.
-
 -
дистрибутивно относительно +.
-
дистрибутивно относительно +.
Пример:
(Z,+, )
– множество квадратных матриц (nxn)
над
полем Z.
)
– множество квадратных матриц (nxn)
над
полем Z.
Опр:
Поле – коммутативное кольцо с е, в
котором каждый ненулевой элемент имеет
обратный по умолчанию.
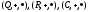
Опр:
Гомоморфизм – группы
 - такое отображение множества G
в
K,
при котором
- такое отображение множества G
в
K,
при котором
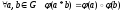 .
Если
.
Если
 - биективное отображение G
- биективное отображение G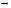 K,
то
K,
то
 - изоморфизм группы и гомоморфизм колец
- изоморфизм группы и гомоморфизм колец
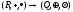
Утв:
Пусть
 - изоморфизм
- изоморфизм
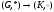 тогда:
тогда:
Доказательство:
-
Пусть
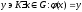 ,
т.к.
,
т.к.
 - биекция.
- биекция.

-

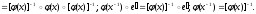
Опр:
Конгруэнция на множестве Х с операцией
* - (Х,*) – отношение эквивалентности р
на Х со свойствами:
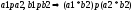 .
Говорят,
что отношение р согласовано с операцией
*.
.
Говорят,
что отношение р согласовано с операцией
*.
Утв: Пусть р – отношение эквивалентности на множестве (Х,*), тогда определим операцию на классах эквивалентности, положив результат: [a]p*[b]p=[a*b]p, тогда данная операция определена корректно, т.е. не зависит от выбора элементов из [a]p, [b]p.
Доказательство:
Пусть
 надо
показать, что [x*y]p=[a*b]p.
надо
показать, что [x*y]p=[a*b]p.
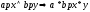 ,
т.к.
р – конгруэнция
,
т.к.
р – конгруэнция
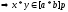 ,
т.к.
р – отношение эквивалентности, а по Т1
,
т.к.
р – отношение эквивалентности, а по Т1
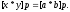
Теорема:
Пусть
 - гоморфизм тогда:
- гоморфизм тогда:
-
 -
группа
-
группа -
р на G вида:
 конгруэнция
конгруэнция -
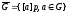 ,
тогда
,
тогда
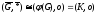 (* - оператор на классах)
(* - оператор на классах)
Доказательство:
-
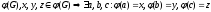
-
 ,
т.е. задана операция.
,
т.е. задана операция. -
Она ассоциативна т.к.
 ,
а
К – группа
,
а
К – группа
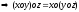
-
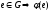 -
единица
-
единица

-
-
р – отношение эквивалентности на G:
-
 -
рефлективное
-
рефлективное -
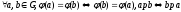
-
 -
транзитивность
-
транзитивность
-
Проверим согласованность р со *:
 т.к
т.к
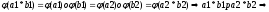 р – конгруэнция.
р – конгруэнция.
-
 ,
где
,
где
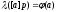 - покажем что это отображение задано
корректно:
- покажем что это отображение задано
корректно:-
 ,
т.е. отображение задано корректно.
,
т.е. отображение задано корректно. -
 -
изоморфизм?
-
изоморфизм?
-
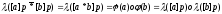 ,
т.е.
,
т.е.
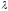 - гомоморфизм.
- гомоморфизм.
-
Суръективность:

-
Инъективность:
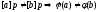
От
противного: Пусть
 - изоморфизм
- изоморфизм
Следствие:
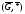 - группа, т.к. изоморфно
- группа, т.к. изоморфно
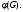
Элементы теории групп.
Опр:
Пусть
 - группа: е – определен однозначно и
- группа: е – определен однозначно и
 - однозначен.
- однозначен.
Доказательство:
-
Пусть е1, е2 – единичные элементы, тогда е1=е1*е2=е2
-
 обратные
к х, тогда х*х1=е, х*х2=е =>
х*х1=х*х2
обратные
к х, тогда х*х1=е, х*х2=е =>
х*х1=х*х2

Опр:
Пусть
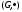 - группа, тогда Н – подгруппа группы G,
если:
- группа, тогда Н – подгруппа группы G,
если:
-
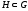
-
 -
сама группа.
-
сама группа.
Пример: Z<Q<R<C
Теорема:
Пусть
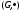 - группа, тогда подмножество H<G
- группа, тогда подмножество H<G
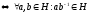 - “Критерий
быть подгруппой”.
- “Критерий
быть подгруппой”.
Доказательство:
-
 -
группа
-
группа
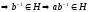
-
Обратно:
-
т.к.
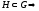 ассоциативность
из G
в Н, т.е
ассоциативность
из G
в Н, т.е
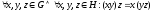
-
е группы
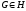 .
Пусть
a=e,
b=x
.
Пусть
a=e,
b=x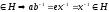
-
Замкнутость: Пусть
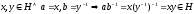
-
Теорема:
Множество G
с внутренней бинарной ассоциативной
операцией – группа. Тогда, когда в этом
множестве
 однозначно разрешимы уравнения: ax=b,
ya=b.
однозначно разрешимы уравнения: ax=b,
ya=b.
Доказательство:
-
ax=b;
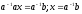 - однозначно, т.к.
- однозначно, т.к.
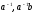 - однозначны.
- однозначны. -
Обратно:
-
Пусть bx=b, т.к
 е1
– решение этого уравнения
е1
– решение этого уравнения
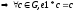
-
 ,
т.е оба решения совпадают: е1=е2=е, т.е.
,
т.е оба решения совпадают: е1=е2=е, т.е.

-
 -
решения. Покажем, что
-
решения. Покажем, что

-
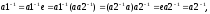 т.е.
т.е.
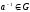
-
единственность е и
 ,
т.к.
уравнения разрешимы однозначно: ах=а,
е – решение =>
е – однозначно, ах=е,
,
т.к.
уравнения разрешимы однозначно: ах=а,
е – решение =>
е – однозначно, ах=е,
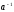 - решение =>
- решение =>
 - однозначно.
- однозначно.
Свойства отображений конечных множеств.
Пусть
 - множество,
- множество,
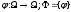 .
.
Опр:
Пусть
 - отображения
- отображения
 - композиция
- композиция
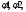 если
если
 т.е.
т.е.
 ;
т.е.
;
т.е.
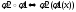
Произведение
отображений:
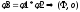 - полугруппа.
- полугруппа.
Утв:
Операция: композиция отображения – на
некотором множестве
 - ассоциативна, т.е.
- ассоциативна, т.е.
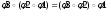 .
.
Док-во:
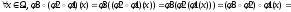
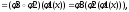 т.е.
отображения совпадают.
т.е.
отображения совпадают.
Следствие: Множество (Ф,о) – полугруппа с е. е тождественное отображение.
Теорема:
Пусть В – множество взаимно однозначных
отображений множества
 ,
т.е. (В,о) =>
(В,о) – группа.
,
т.е. (В,о) =>
(В,о) – группа.
Док-во:
-
(В,о) – полугруппа
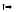
-
Отображение элементов? Пусть
 если
если
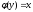 .
.
Задача: Равенство – БО, удовлетворяющее 1 – 4?
Задача: БО не удовлетворяет 1 – 4? X={1, 2, 3}; p={(1,1),(2,3),(3,2),(1,3)}.
-
Не выполняется т.к. нет (2,2) – хотя бы.
-
Не выполняется т.к. нет (3,1) – хотя бы.
-
Не выполняется т.к. нет (1,3),(3,2) => (1,2)
-
Не выполняется т.к. нет (3,2),(2,3) => (2,2)
Задача: Мультипликативная группа положительных вещественных чисел изоморфна аддитивной группе всех вещественных чисел?
-
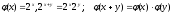 -
изоморфизм, или f(x)=lnx;
ln(x+y)=lnx+lny.
-
изоморфизм, или f(x)=lnx;
ln(x+y)=lnx+lny. -
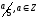 -
группа по сложению. По умножению нет!
(не замкнута).
-
группа по сложению. По умножению нет!
(не замкнута).
Задача:
Доказать, что множество
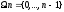 с операцией
с операцией
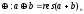 - остаток от деления на n.
- остаток от деления на n.
-
Замкнутость очевидна т.к. res < n.
-
Ассоциативность:
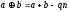
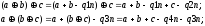
а
т.к.
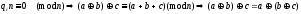
-
e - ? => e=0, т.к.
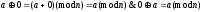
-
Обратно: е=0, т.к.
 т.к.
т.к.
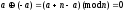
Задача:
Изоморфизм
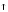 этой группы с группой всех корней энной
степени из 1.
этой группы с группой всех корней энной
степени из 1.
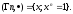
Пусть

-
Взаимное соответствие – в обоих по n элементов.

-