Завдання 5. Біноміальний закон розподілу
Приклад 9. Прилад складається з трьох незалежно працюючих елементів. Ймовірність того, що елемент не працює в довільний момент часу, дорівнює 0,1. Дискретна випадкова величина Х – число елементів, що не працюють у довільний момент часу, розподілена за біноміальним законом розподілу. Необхідно:
Знайти ряд розподілу Х.
Побудувати многокутник ймовірностей.
Знайти , , .
Знайти найімовірніше значення величини Х.
Обчислити ймовірність попадання випадкової величини в задані інтервали
,
,
.
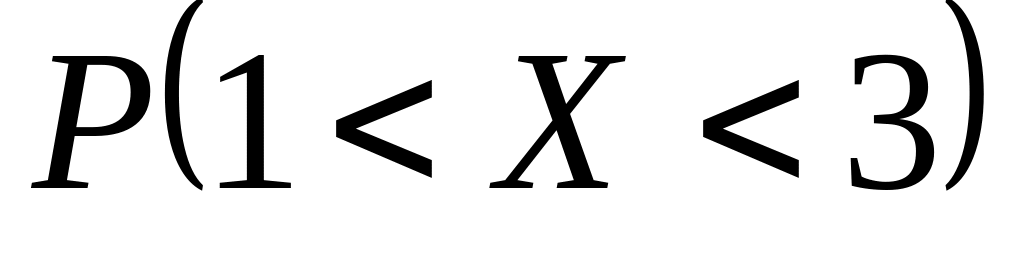Розв'язання: Зробимо аналіз задачі та визначимо, які конкретні значення може набути ДВВ Х. Серед трьох незалежно працюючих елементів число елементів, що не працюють у довільний момент часу, може дорівнювати 0 (всі елементи працюють), 1 (не працює один елемент), 2 (не працює два елементи) або 3 (всі елементи не працюють).
У табличній формі закон розподілу цієї дискретної випадкової величини можна записати:
|
0 |
1 |
2 |
3 |
|
|
|
|
|
Обчислимо
ймовiрностi
,
застосовуючи формулу Бернуллі. Враховуючи,
що за умовою задачі
,
(значить,
),
маємо:
,
,
,
.
Занесемо одержані значення в таблицю та перевіримо обчислення за властивістю ряду розподілу:
|
0 |
1 |
2 |
3 |
|
0,729 |
0,243 |
0,027 |
0,001 |
.
Будуємо многокутник розподілу (рисунок 15):
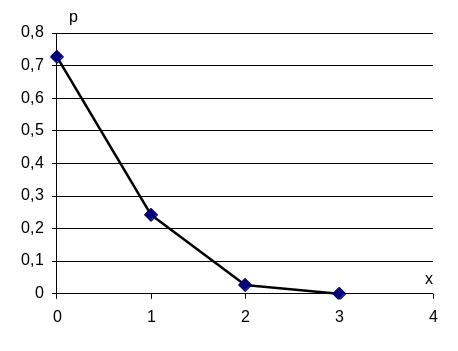
Рисунок 15
Обчислюємо числові характеристики:
,
,
.
Знайдемо
найімовірніше значення
величини Х
із
нерівності:
.
Тоді
,
.
Значить,
найімовірнішим значенням величини Х
є нуль і
.
Обчислимо
ймовірності попадання випадкової
величини в задані інтервали
,
,
.
=0,
=
,
.
ЗАДАЧІ
Дискретна випадкова величина Х розподілена за біноміальним законом розподілу. Необхідно:
Знайти ряд розподілу Х.
Побудувати многокутник ймовірностей.
Знайти , , .
Знайти найімовірніше значення величини Х.
Обчислити ймовірність попадання випадкової величини в задані інтервали ,
,
.
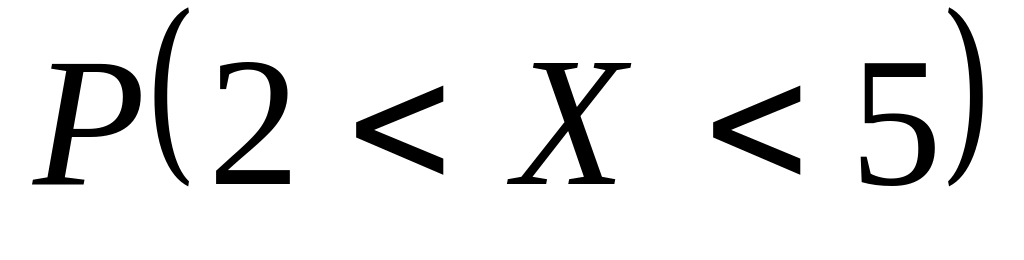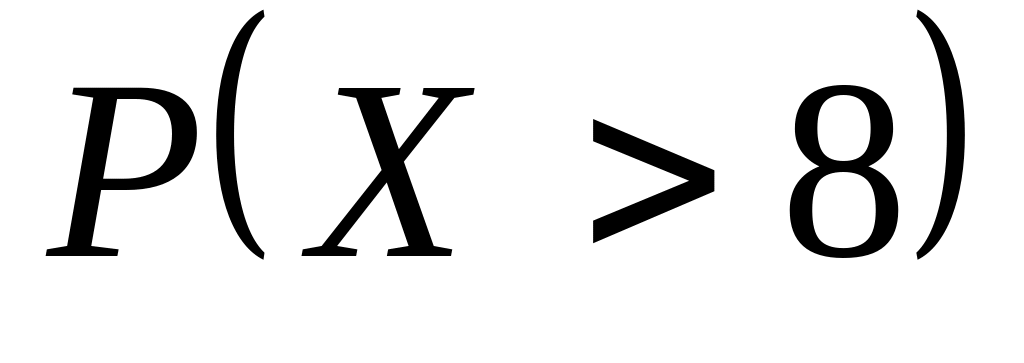3.1. Робітник виготовляє однотипні деталі. Відомо, що при виготовленні однієї деталі ймовірність допустити брак дорівнює 0,1. Навмання беруть 10 деталей. ДВВ Х – число стандартних деталей серед десяти взятих навмання.
3.2. Маємо партію дисків. Ймовірність того, що навмання взятий диск виявиться бракованим, дорівнює 0,01. Навмання беруть 10 дисків. ДВВ Х – кількість дисків, що пройшли контроль.
3.3. В комп’ютерному залі 15 ПК. Ймовірність виходу комп’ютерної мишки з ладу за рік роботи 0,3. ДВВ Х – кількість комп’ютерних мишок, що вийшли з ладу за рік.
3.4. В урні міститься 6 чорних та 4 білих кулі. Кулі виймаються навмання по одній з повертанням. Провели дев’ять виймань. ДВВ Х – кількість чорних куль серед дев’яти вилучених навмання.
3.5. В ящику містяться 12 деталей 1-го сорту, 3 деталі 2-го сорту, 4 деталі браковані. Деталі вилучають по одній з повертанням. Провели десять вилучень. ДВВ Х – число придатних деталей при десяти вилученнях.
3.6. На склад магазину надійшли нові вироби, 80% яких вищого ґатунку. Навмання беруть вісім виробів. ДВВ Х – кількість виробів вищого ґатунку серед восьми взятих навмання.
3.7. Контролер перевіряє вироби на стандартність. Ймовірність того, що стандартний виріб контролером буде виявлений придатним, постійна і дорівнює 0,9. Контролером було перевірено десять виробів. ДВВ Х – число стандартних виробів, виявлених придатними.
3.8. Ймовірність того, що покупець, який зайшов до магазину, щось купить, дорівнює 0,1. Магазин відвідали дев’ять покупців. ДВВ Х – кількість покупців, що зробили купівлю.
3.9. Прилад складається з десяти незалежно працюючих елементів. Ймовірність того, що елемент працює в довільний момент часу, дорівнює 0,9. ДВВ Х – число елементів, працюючих у довільний момент часу.
3.10. Маємо вісім однакових ящиків. В кожному з них знаходиться по 9 стандартних і одній бракованій деталі. З кожного ящика беруть по одній деталі. ДВВ Х – кількість стандартних деталей серед восьми вилучених.
3.11. Гральний кубик кидається 10 разів. ДВВ Х − число разів появи грані з цифрою шість.
3.12. Монета кидається 11 разів. ДВВ Х – число разів випадання цифри.
3.13. Працівник обчислювального залу перевіряє дискети на наявність вірусів. Ймовірність наявності вірусу на дискеті 0,05. Перевіряється 10 дискет. ДВВ Х – кількість заражених вірусом дискет.
3.14. В коробці лежать 5 червоних та 8 білих куль. Кулі виймаються навмання по одній з повертанням. ДВВ Х – кількість білих куль серед 9 витягнутих.
3.15. Ймовірність того, що покупець, який зайшов у супермаркет, зробить покупки, дорівнює 0,3. ДВВ Х – число покупців, що зробили покупку серед 10 навмання взятих.
3.16. В комп’ютерному залі 12 ПК. Ймовірність виходу ПК з ладу при зміні напруги дорівнює 0,03. ДВВ Х – кількість ПК, які вийшли з ладу в результаті зміни напруги.
3.17. В ящику міститься 3 диски CD-RW та 7 дисків CD-R. Диски витягуються по одному з поверненням. ДВВ Х – кількість дисків CD-R серед 10 витягнутих.
3.18. Кожен з програмістів допускає помилку при складанні програми з ймовірністю 0,1. ДВВ Х – кількість програмістів, що допустили помилку серед 12 взятих навмання.
3.19. Ймовірність успішного виконання вправи спортсменом 0,6. ДВВ Х – кількість спортсменів, що успішно виконали вправи серед 9 навмання взятих.
3.20. Ймовірність успішного завантаження WEB-документа в бізнес-час дорівнює 0,15. ДВВ Х – кількість WEB-документів успішно завантажених на 10 ПК.
3.21. Студент вивчив 20 білетів із 30. Білети вилучаються по одному з повертанням. Зроблено 12 спроб. ДВВ Х – кількість вивчених білетів серед 12 взятих.
3.22. При підготовці текстового документа на ПК користувач допускає помилку на сторінці А4 з ймовірністю 0,25. Підготовлено 10 сторінок. ДВВ Х – кількість сторінок без помилок.
3.23. В коробці знаходиться 5 дискет виробництва Sony та 7 дискет виробництва TDK. Дискети виймаються по одній з повертанням. ДВВ Х – кількість дискет виробництва Sony серед 10 витягнутих навмання.
3.24. В ящику міститься 7 стандартних і 3 браковані деталі. Деталі вилучають по одній з повертанням. Виконали десять вилучень. ДВВ Х – кількість стандартних деталей серед десяти вилучених навмання.
3.25. Гральний кубик кидається 8 раз. ДВВ Х − число разів появи грані з цифрою чотири.