Формирование и учет краевых условий задачи пластичности, решаемой методом мкэ в изотермической постановке.

1.Учет внешних сил в основной системе МКЭ.

2.Учет сосредоточенных сил.

3.Учет распределенных сил.

4.Формирование и учет силовых граничных условий при их изначально неизвестных значениях.

5.Формирование и учет кинематических граничных условий.

6.Решение основной системы мкэ методом Гаусса.

Краевыми условиями задачи пластичности называют распределения в заготовке температуры, напряжений, деформаций на начальный момент времени и заданные на ее поверхности внешние нагрузки: сосредоточенные силы; напряжения; распределение температуры; перемещения или скорости материальных точек.

При изотермической постановке задачи изменение температуры не рассчитывается, а изменением свойств металла, обусловленным изменением температуры пренебрегают, т.е. тепловой эффект пластической деформации не учитывается. Инструмент при моделировании процессов развитой пластической деформации считается абсолютно твердым телом. Начальные температурные условия для всех конечных элементов и всех этапов нагружения модели одинаковы.

При использовании деформационной теории пластичности задача пластичности решается за один этап нагружения конечно-элементной модели. При этом модель нагружается полной нагрузкой.

При использовании теории течения в приращениях перемещений, теории течения в скоростях моделирование формоизменения заготовки осуществляется путем последовательного решения задач пластичности. Для каждой задачи формируют краевые условия, соответствующие этапу нагружения конечно-элементной модели. При этом модель на каждом очередном этапе нагружается частью от полной нагрузки.

При изотермической постановке задачи используются диаграммы деформирования или графики скоростного упрочнения соответствующие металлу заготовки и температуре операции. Диаграммы одинаковы для всех элементов. Обычно диаграмма деформирования указывается в программе в виде функциональных зависимостей.

Например:

,при ;

, при ,

где - интенсивность напряжений;

- интенсивность деформаций;

0.002 – предельное значение упругой деформации для большинства металлов;

Н – линейный модуль упрочнения металла.

Аналитические зависимости, описывающие диаграммы не содержат температуру.

Модель среды обычно перед первым нагружением считается ненапряженной и недеформированной, т.е. в каждом конечном элементе компоненты матриц напряжений и деформацийn-го элемента на начальный момент времени равны 0.

Начальные условия в части напряжений и деформаций для второго и последующих этапов нагружения отличны от 0 и равны напряжениям и деформациям, рассчитанным на предыдущем этапе нагружения:

.

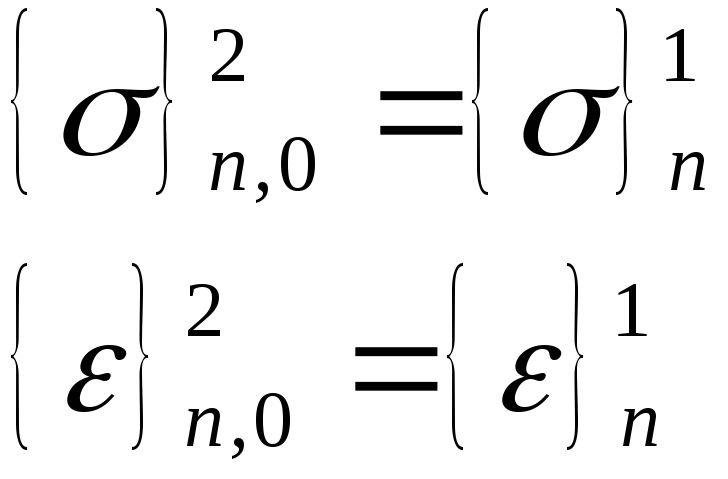Перед каждым этапом нагружения модели, кроме начальных условий формируются силовые и кинематические условия для граничных узлов конечно-элементной модели.

В случае заданной сосредоточенной силы, действующей на i-ый узел, определяются проекции этой силы на оси координат:

;

где - узловая сила;

- углы наклона вектора к осям координат.

Рассчитанные компоненты силы заносятся в правую часть основной системы МКЭ , т.е. в матрицу-столбец нагрузки. При этом номер строки, куда помещается компонента, определяется номером узла и размерностью задачи.

Двумерная задача:

-ая строка -ая строка.

Трехмерная задача:

-ая строка ;-ая строка ;-ая строка.

При поэтапном решении задачи:

-ая строка ;-ая строка и т.д,

k– количество этапов нагружения модели , выбирается исследователем.

В случае задания распределенной нагрузки методика учета аналогична выше изложенной. Отличие состоит в предварительном сведении распределенной нагрузки к узлам.

Двумерная задача рис.1

Рис.1.К определению силовых граничных условий при распределенной нагрузке на поверхности заготовки: ,– касательное и нормальное напряжения, заданные на поверхности граничного элемента 1;– нормальное напряжение, заданное на поверхности граничного элемента 2;– касательное и нормальное напряжения, заданные на поверхности граничного элемента 3.

,

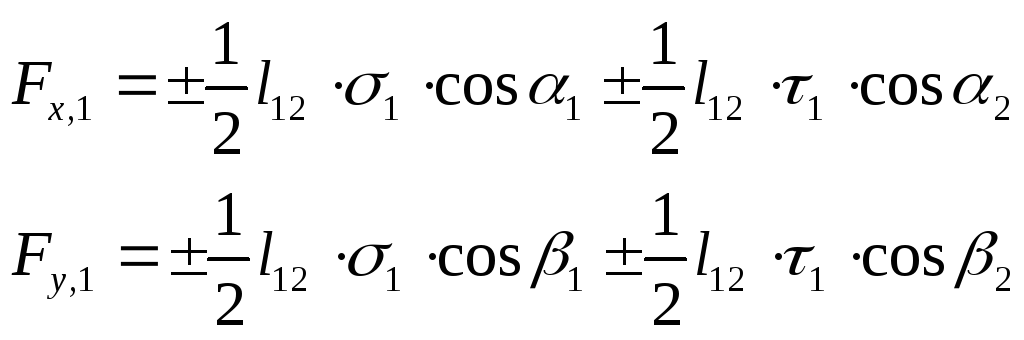- длина стороны треугольного конечного элемента;

- угол между нормалью к стороне элемента 1 и осью абсцисс;

- угол между стороной элемента 1 и осью абсцисс;

- угол между нормалью к стороне элемента 1и осью ординат;

- угол между стороной элемента 1. и осью ординат;

.

Для узла 2 учитываются вклады распределенных нагрузок, приложенных уже к двум элементам.

Аналогично для узла 3:

.

Осесимметричная задача (кольцевые конечные элементы)

Рис.2. К определению силовых граничных условий при использовании кольцевых конечных элементов:- распределенная по кольцевой поверхности элемента 1 касательная нагрузка;- распределенная по боковой поверхности усеченного конуса (это граничная поверхность элемента 2) нормальная нагрузка;- распределенная по граничной поверхности элемента 3 нормальная нагрузка.

,

где - угол между образующей поверхности кольцевого элемента 1 и осью (оr); - угол между образующей поверхности кольцевого элемента 1 и осью аппликат.

где - угол наклона нормали образующей кольцевого элемента 2 к оси (оr); - угол наклона нормали образующей кольцевого элемента 2 к оси аппликат.

где - угол наклона нормали образующей кольцевого элемента 3 к оси (оr); - угол наклона нормали образующей кольцевого элемента 3 к оси аппликат.

Знаки перед слагаемыми выражений узловых сил определяются знаками проекций распределенных нагрузок на соответствующие оси координат.

При решении трехмерной задачи и использовании объемных конечных элементов сведение распределенных нагрузок к узловым силам, осуществляется аналогично:

;

где m=x,y,z; l – количество граничных, нагруженных распределенной нагрузкой конечных элементов соприкасающихся в i- ом узле;,- распределенные нагрузки, действующие на граниj - го конечного элемента;- площадь граниj - го конечного элемента; - угол наклона нормали нагруженной грани конечногоj - го элемента к оси абсцисс; - угол наклона вектора касательной силы, действующей по граниj – го элемента к оси абсцисс (вектор силы на скрещивающейся прямой к оси абсцисс); k – количество узлов грани j – го элемента.

В случае m=y и m=z углы ,- углы наклона соответственно к оси ординат и оси аппликат.

Формирование и учет силовых граничных условий при их изначально неизвестных значениях.

Обычно этот случай имеет место, когда заданы неявно кинематические ограничения.

Например, известно, что материальные частицы должны перемещаться (значения перемещений неизвестны) вдоль поверхности матрицы (вдоль контактной линии описывающей образующую матрицы) (рис.3).

Рис.3. К формированию силовых граничных условий, при задании неявного кинематического условия:dN1,dN2 – приращения нормальных сил в узлах 1 и 2;

dT1, dT2 – приращения касательных сил в узлах 1 и 2.

Выполнение условия перемещения узлов 1 и 2, вдоль контактной линии очевидно возможно при определенных значениях приращений перемещений и приращений узловых сил.

где - приращения перемещений узлов 1 и 2 вдоль осей координат.

Приращения узловых сил на 1 – ом этапе нагружения модели неизвестны. Поэтому поступают следующим образом.

На 1 – ом этапе нагружения этим приращениям присваивают малые значения.

dN1=dN2=10Н.

dT1=dT2=1Н.

Следует отметить, что в качестве касательных узловых приращений сил обычно выступают приращения сил распределенного приращения напряжения трения.

Но ∆- приращение напряжения контактного трения не всегда (не на каждом этапе нагружения) стоит принимать отличным от 0.

За небольшое количество этапов нагружения модели узловые приращения сил можно привести в соответствие с условием скольжения узлов по контактной линии. Для этого значения приращений узловых сил перед каждым этапом нагружения модели корректируются по выражениям:

где

где k - номер этапа нагружения конечно-элементной модели.

Следует отметить, что в качестве касательных узловых приращений сил обычно выступают приращения сил трения.

Но ∆- приращение напряжения контактного трения не всегда (не на каждом этапе нагружения) стоит принимать отличным от 0.

если имеет место «упрочнение» элементов окружающих 1 – ый и 2 – ой узлы , k - номер этапа нагружения конечно-элементной модели.

Узловые приращения (правые части, соответствующих уравнений равновесия) сил рассчитывают по выражениям:

где - угол наклона нормали контактной линии к оси (оr) ,

- угол наклона контактной линии к оси (о r),

- угол наклона нормали контактной линии к оси (о x),

- угол наклона контактной линии к оси (о x).

Кинематические граничные условия формируются с учетом используемой теории пластичности, полного перемещения инструмента, геометрической формы подвижного и неподвижного инструментов и условий движения материальных частиц относительно инструмента.

Задать кинематическое граничное условие для узла это означает указать и учесть следующее.

В случае использования теории течения в скоростях узловые компоненты скоростей узла вдоль осей координат. Эти компоненты рассчитываются с учетом скорости инструмента (оборудования)– скорости деформирования соответствующей данному этапу пластического формоименения заготовки или приравниваются 0 в случае принятия условия «прилипания» (см. рис.4).

Рис.4.К формированию граничных кинематических условий:

- скорость деформирования на данный момент времени формоизменения заготовки при осадке.

( в случае задания условия прилипания на 1-ый узел);

;

;

;

( в случае задания условия прилипания на 4-ый узел);

( 4-ый узел соприкасается с неподвижной плитой);

;

.

-определяются, как и скорости всех других узлов конечно- элементной сетки путем решения основной системы МКЭ.

Система МКЭ решается после учета в ней силовых и кинематических граничных условий.

Первый способ учета граничного условия в i-ом узле.

Все компоненты, кроме диагональной, строки матрицы жесткости соответствующей граничному условию обнуляются. Диагональная компонента приравнивается 1 , а правая часть уравнения соответствующего этой строке приравнивается значению ограничения .

Например, в соответствии с рис.4 (задачу для определенности будем считать плоской):

Узлу 1 соотвествуют:1-ая и 2-ая строки матрицы жесткости и правая часть F1, поэтому:

,

где n=2*kol_uzlov.

, ,.

Узлу 2 соответствуют: 3-ая и 4-ая стороны матрицы жесткости.

,

3-ю строку матрицы не трогаем, т.к. граничное условие не задано.

Узлу 3 соответствуют 5-ая и 6-ая строки, 5-ую строку матрицы не изменяем:

,,

Узлу 4:

,,

,,

Узлу 5:

,,

Узлу 6:

,,

Таким образом, если задано условие и, то:

Второй способ учета граничного условия в i-ом узле.

Все компоненты,кроме диагональной, строки матрицы жесткости, соответствующей граничному кинематическому условию обнуляются.

Правая часть уравнения соответствующего этой строке приравнивается произведению значения ограничения на неизмененную диагональную компоненту строки.

Например, рис.4:

Узел 1:

.

Узел 2:

Узел 3:

,

Узел 4:

,

,

Узел 5:

,

Узел 6:

,

Таким образом, если задано условие и учет производится по способу 2 , то:

Система МКЭ в которой учтены силовые и кинематические граничные условия задачи в дальнейшем решается, и рассчитанные корни, соответствующие узлам с кинематическими ограничениями, будут равны значениям указанных ограничений.

В случае использования теории течения в приращениях перемещений указываются и учитываются значения приращений перемещений (не полные перемещения, а только их части). Значение части от полного перемещения выбирается исследователем.

Например (см. рис.4), абсолютное обжатие при осадке составляет 10 мм.

Принимаем решение - моделировать формоизменение осаживаемой заготовки за 1000 этапов нагружения конечно-элементной модели. После этого решения можно определить значение приращения перемещения граничных узлов вдоль оси OY:

( в случае задания условия прилипания на узел),

Учет ограничений в приращениях перемещений осуществляется аналогично зависимостям (1) или (2) . Отличие заключается в замене значений скоростей на значения приращений перемещений узлов.

Основная система МКЭ может решаться различными способами.

Корнями системы являются перемещения узлов или приращения перемещений, или скорости узлов вдоль осей координат.

( прямой ход- построение треугольной матрицы).

for k:=1 to 2*kol_uzlov do

begin

for j=k+1 to 2*kol_uzlov do

st[k][j]:= st[k][j]/ st[k][k]; rhs[k]:= rhs[k]/st[k][k]; st[k][k]:=1;

for i:=k+1 to 2*kol_uzlov do

begin

for j:=k+1 to 2*kol_uzlov do

begin

if ((st[i][k]<>0) and (st[k][j]<>0)) then

st[i][j]:= st[i][j]- st[i][k]* st[k][j];

end;

rhs[i] :=rhs[i] - st[i][k]* rhs[k]; end;end;

(обратный ход – расчет корней системы)

ux[2*kol_uzlov ]:= rhs[2*kol_uzlov ]/ st[2*kol_uzlov][ 2*kol_uzlov];

for i:= 2*kol_uzlov-1 down to 1 do

begin

ж :=0;

for j=i+1 to 2*kol_uzlov do

begin

if st[i][j]<>0 then

ж:=ж+st[i][j]*ux[j];

end;

ux[i]:= rhs[i]-ж;

end;

rhs - правая часть уравнения ,

ux - корень уравнения (массив корней системы).