Конечного элемента

Далее необходимо сложить все три матрицы:

.

Для сравнения запишем пятую строку матрицы [K]:

12+0+34 12+0+34 12+20+0 12+20+0 12+20+34 12+20+34

20+0 20+0 34 34.

Или [46, 46, 32, 32, 66, 66, 20, 20, 34, 34]. (2)

Из сравнения строк (1) и (2) видно, то они совпадают.

Процедура формирования матрицы ([К]) способом объединения по элементам приведена ниже.

Procedure Rachet_matrSt;

Var m1, m2, m3, m4, m5, m6:byte;

Begin

for i:=1 to 2*kol_uzlov do

for j:=1 to 2*kol_uzlov do

st[i]^[j]:=0;

for k:=1 to kol_elem do

begin

m1:=nod[k,1]*2-1;

m2:=nod[k,1]*2;

m3:=nod[k,2]*2-1;

m4:=nod[k,2]*2;

m5:=nod[k,3]*2-1;

m6:=nod[k,3]*2;

st[m1]^[m1]:=ste[k,1,1]+st[m1]^[m1];

………………………………………..*4 раза

st[m1]^[m6]:=ste[k,1,6]+st[m1]^[m6];

st[m2]^[m1]:=ste[k,2,1]+st[m2]^[m1];

…………………………………………*4 раза

st[m2]^[m6]:=ste[k,2,6]+st[m2]^[m6];

…………………………………………*18 раз

st[m6]^[m1]:=ste[k,6,1]+st[m6]^[m1];

…………………………………………*4 раза

st[m6]^[m6]:=ste[k,6,6]+st[m6]^[m6];

end;

end.

Матрицы дифференцирования, упругости, упруго-пластичности.

1.Матрицы при расчёте плоского деформированного состояния.

2.Матрицы при расчёте осесимметричного Н.Д.С.

3.Матрицы при расчете трехосного Н.Д.С.

Треугольный конечный элемент (рис.4.1).

Рис.4.1

Матрица жёсткости элемента: ,

Матрица дифференцирования элемента:

, где ,,.

Матрица упругости: ,

где -коэффициент пуассона,-модуль упругости первого рода.

Матрица упруго-пластичности (при решении задачи в приращениях перемещений):

,(1)

где

,

,,

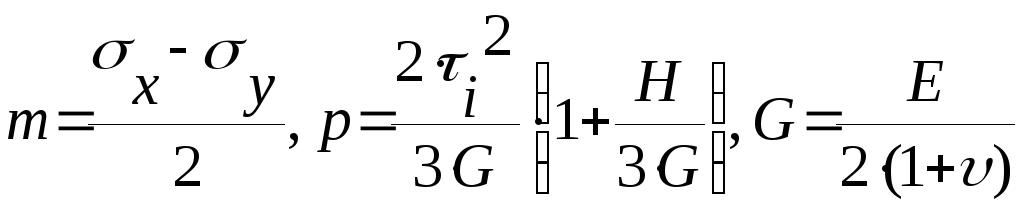- касательный модуль упрочнения.

Матрица упругости (плоское напряжённое состояние):

, .

Матрицу (1), как и другие матрицы получают путём матричного представления соответствующих уравнений связи напряжений (приращений напряжений) и деформаций (приращений деформаций).

Например, в теории течения в приращениях эти уравнения имеют вид: ,

где:

, ,.

Для решения вопроса перехода материальной частицы из пластического состояния в упругое состояние, оценивают величину d:

где  = 0 для упругих зон,  =1 для упругопластичных зон.

Если d 0 материальная частица считается перешедшей из пластического состояния в упругое состояние.

При решении вопроса перехода материальной частицы из упругого состояния в пластическое проверяют неравенство: = 0,

где- интенсивность напряжений,- мгновенный предел текучести соответствующий накопленной деформации, гдеколичество шагов нагружения материальной частицы,- интенсивность приращений деформаций на k-ом шаге нагружения материальной частицы.

Если неравенство выполняется, материальная частица перешла в упругопластическое состояние. Если выполняется неравенство , то напряжённое состояние материальной частицы, рассчитанное с упругой матрицей или упругопластической, считается рассчитанным (удовлетворяющим диаграмме деформирования, уравнениям связи).

- величина, которая принимается исследователем одинаковой для всех шагов нагружения частицы, например (=0,03).

Кольцевые конечные элементы с треугольным поперечным сечением (рис.4.2).

Рис.4.2

Матрица жёсткости кольцевого конечного элемента:

Матрица дифференцирования:

,

где, ,,,.

компоненты третьей строки матрицы зависят от r и z, их приравнивают среднеарифметическим значениям: .

Матрица упругости:

.

Матрица упругопластичности (при решении задачи в приращениях перемещений):

-

,

где ,,,

.

Объёмный конечный элемент- тетраэдр (рис.4.3):

Рис.4.3

При перечислении номеров узлов следует придерживаться определённого порядка. Начиная, например, с Р-го узла остальные номера узлов указываются в направлении по часовой стрелке (p j I m). Если смотреть со стороны последнего узла, то первые три узла обходятся против часовой стрелки (правило правой руки).

Объем элемента: .

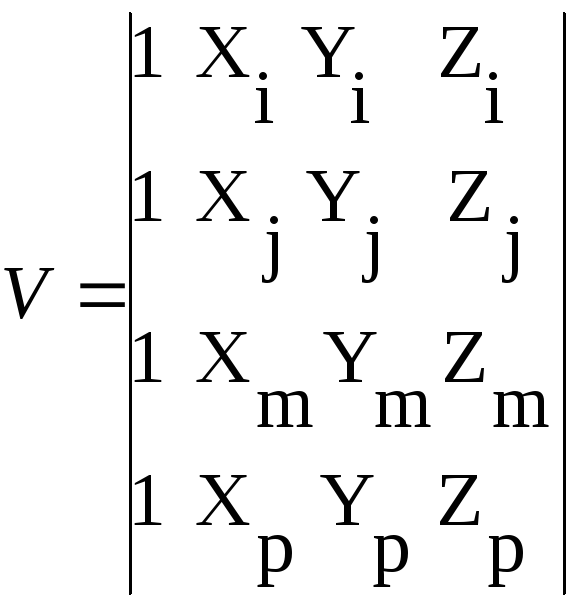Матрица дифференцирования (для порядка i j m p):

,

где

, ,,.

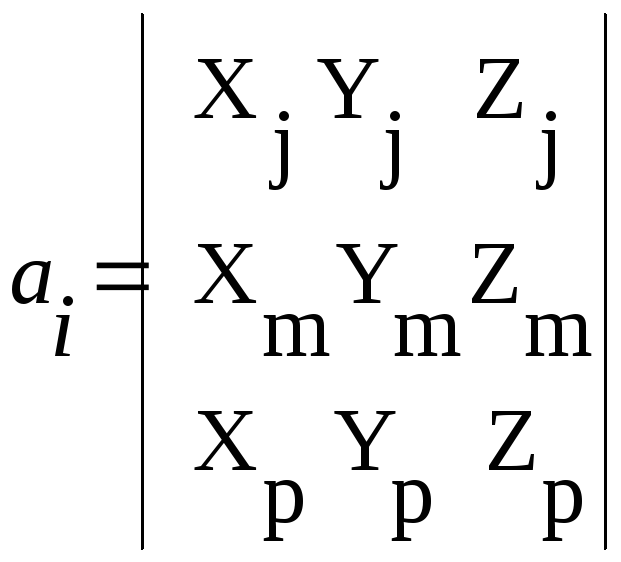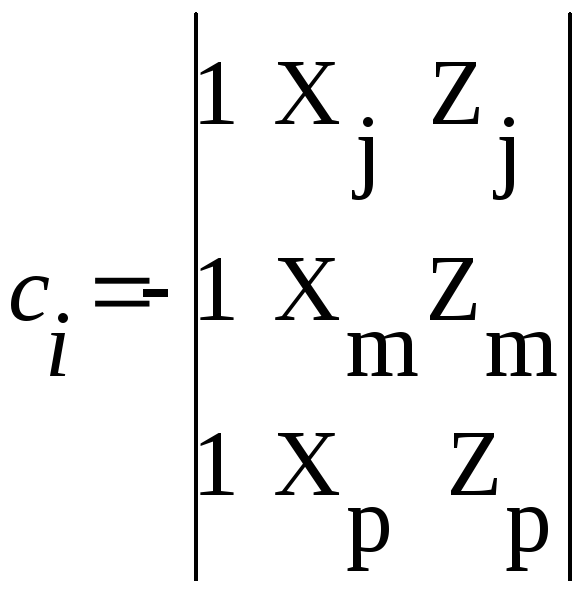Другие компоненты получаются циклической перестановкой индексов.

Упругая матрица в соответствии с законом Гука в случае изотропного тела имеет вид:

Упругопластическая матрица в соответствии с теорией течения в приращениях для трехмерного случая имеет вид:

,

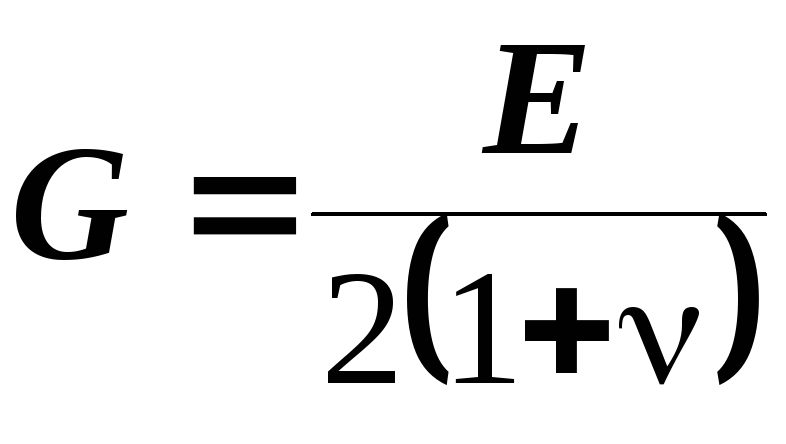
где ; ,  интенсивность касательных напряжений;  компоненты девиатора напряжений; H  касательный модуль (угол наклона касательной к оси O_i в точке диаграммы деформирования, соответствующей текущему напряженному состоянию конечного элемента) упрочнения;  модуль сдвига;   коэффициент Пуассона.

Переход элемента из пластического состояния в упругое состояние характеризует величина d:

,

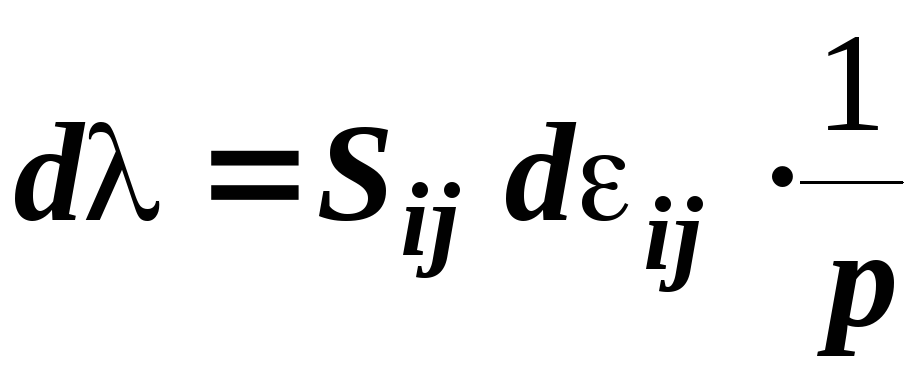где  компоненты девиатора приращений деформаций.

линеаризации задач пластичности при ее решении методом МКЭ).

1. Метод переменных параметров упругости (метод секущих)

2. Метод касательных жесткостей

3. Метод дополнительных деформаций.

Литература:

Н.С.Можаровский, Н.Е. Качаловская. Методы и алгоритмы решения краевых задач.Часть  1991, Киев, Высшая школа.

Метод переменных параметров упругости (метод секущих в случае теории течения в скоростях) основан на представлении уравнений связи напряжений и деформаций в форме уравнений теории упругости, в которых параметры упругости зависят от достигнутого НДС:

, где

- матрица-столбец напряжений n-го конечного элемента;

- матрица упруго-пластичности, для плоского деформированного состояния имеет вид:

Компоненты матрицы , их порядок расположения в матрице соответсвует матрице. Метод применяется, когда модель нагружается полной нагрузкой за один шаг нагружения.

Порядок реализации метода хорошо виден на рис.1.

Рис.1 Схема к уточнению переменных параметров упругости

Рассмотрим алгоритм определения НДС двух конечных элементов. Один из элементов пусть будет в упругом состоянии, другой - в упругопластическом.

В первом приближении основная система МКЭ - =решается

в предположении, что все элементы находятся в упругом состоянии, т.е. их матрицы жесткости рассчитываются с применением матриц, в которых

=иE*=E.

Для элемента , находящегося в упругом состоянии после определения его ,иточка с координатами, будет находится на прямолинейном отрезке диаграммы деформирования=f() (см. рис.1). Напряженно-деформированное состояние (НДС) этого элемента считается рассчитанным.

Для 2-го элемента , находящегося в упругопластическом состоянии, точка с координатами будет находится на луче, проведенном из начала координат под угломarctg(Е) к оси абцисс, выше диаграммы деформировани =f().

Если удовлетворяется неравенство: ,

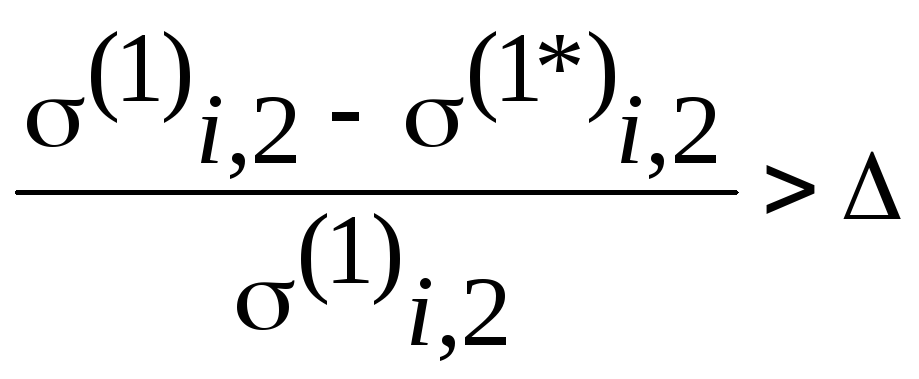где ∆ - некоторая величина, принятая исследователем для всех элементов и приближений одинаковой, то напряженное состояние считается не рассчитанным, и тогда возникает необходимость второго приближения (второго решения системы МКЭ сформированной уже с уточненной матрицей для второго элемента):

После определения НДС во втором приближении точка с координатами окажется на луче, проведенном из начала координат под угломarctg(Е) выше диаграммы=f(), но уже ближе к ней.

Если условие (1) выполняется, то НДС элемента считается рассчитанным. Если не выполняется, то для элемента осуществляется очередное уточнение: Е;, находится новое решение системы МКЭ и т.д., пока не выполнится условие (1).

Метод касательных жесткостей основан на представлении уравнений связи приращений напряжений и приращений деформаций в форме

(2),

где =- упругая матрица,

=- матрица упруго-пластичности, когда элемент находится в упруго-пластическом состоянии.

Компоненты этой матрицы рассчитываются через касательный модуль упрочнения.

Для плоского деформированного состояния

,

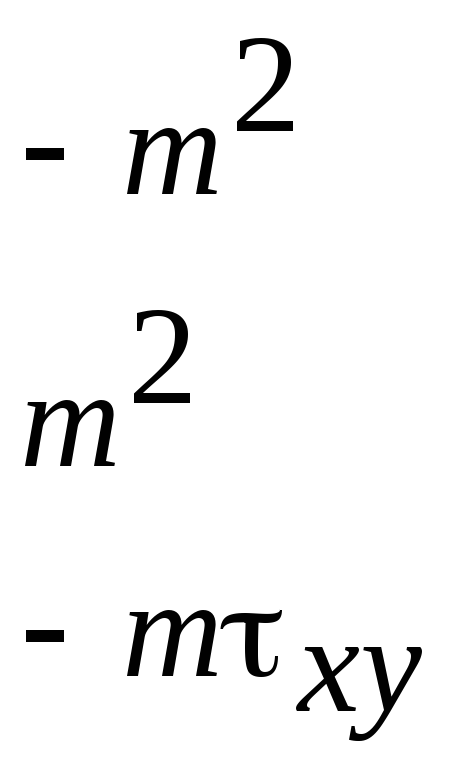
где ;

- интенсивность касательных напряжений;

G – модуль упругости второго рода;

H – касательный модуль упрочнения, ;

m=.

Уравнение (2) иллюстрирует рис.2.

Точке 1 на диаграмме соответствуют:

Рис.2

При очень малых приращениях деформаций по уравнениям (2) можно рассчитать приращения напряжений через m и ,определенные в т.1 (arctg(H)) и окажется ,что точка с координатами (этой точке соответствуютбудет находиться на диаграмме деформирования=f().

Порядок реализации этого метода проследим, наблюдая за одним конечным элементом.

Метод касательных жесткостей применяется, когда модель на каждом шаге расчета нагружается не полной нагрузкой, а только частью от нее. Поэтому элемент в общем случае может сначала пребывать в упругом состоянии, затем, в упругопластичном, затем опять в упругом состоянии и т. д.

Пусть наш элемент на нескольких (k-1) начальных шагах нагружения пребывал в упругом состоянии и его НДС после (k-1)-го шага соответствовало точке, изображенной на рис.3.

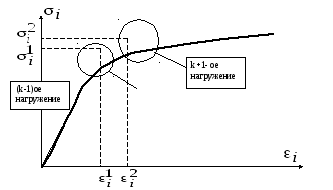
k- ое нагружение

Рис.3

При следующем k-ом нагружении НДС элемента, рассчитанное с упругой матрицей будет изображаться точкой обозначенной стрелкой.

Если условие (1) не выполняется, то для этого элемента рассчитывается - при этомH рассчитывается в точке лежащей на диаграмме, выполняется очередное приближение (решается система:=сформированная с использованием уточненной матрицыдля данного конечного элемента). Вновь определенное НДС элемента будет изображаться точкой, лежащей на диаграмме или выше нее. При этом условие (1) будет выполняться быстрее (т.е. будет наблюдаться сходимость решения) с меньшими порциями нагрузки.

На следующем шаге нагружения матрица для этого элемента берется от предыдущего шага.

Если условие (1) не выполняется, то сначала осуществляют проверку – в каком состоянии находится элемент по параметру :

.

Если < 0, то это означает, что элемент перешел в упругое состояние и для этого элемента в следующем приближении необходимо брать =.

Если > 0, то для этого элемента модульH рассчитывается по точке обозначенной кружком на диаграмме, затем формируется для элемента матрица, формируется и решается в очередном приближении система МКЭ.

Если при данной порции нагрузки сходимости решения нет, величину частичной нагрузки уменьшают.

Метод дополнительных деформаций (дополнительных приращений деформаций) основан на представлении уравнений связи приращений напряжений й приращений деформаций в форме

(3),

где - упругая матрица;

- вектор-столбец приращений дополнительных пластических деформаций;

- вектор-столбец полных приращений деформаций.

Особенностью данного метода по сравнению с предыдущим является то , что при всех приближениях матрицы =для всех элементов являются неизмеными, как и их матрицы жесткости. При каждом приближении уточняется вектор нагрузки. Почему?

Если для какого либо элемента не выполняется условие (1) , то для него рассчитывается (4),

где - касательный модуль упрочнения в точке диаграммыопределенной для конечного элемента наk-1 нагружении ;

- девиатор напряжений в первом приближении на k-ом нагружении элемента;

- интенсивность приращений деформаций для элемента в первом приближении на k-ом этапе нагружения.

В случае нескольких уточнений для одного и того же элемента приращений деформаций по выражению (3) последние складываются.

По рассчитанным (формула (3)) приращениям деформаций рассчитываются дополнительные приращения внутренних узловых сил от каждого конечного элемента,

(5)

Каждый узел сетки окружен различным количеством элементов, и в каждом из них могут иметь место на каком – то приближении приращения деформаций. Поэтому силы, действующие со стороны окружающих элементов на узел и рассчитанные по зависимостям (4) складываются.

Результирующая сила в узле,обусловленная , складывается с соответствующей компонентой вектора нагрузки.

После уточнения по всем узлам система МКЭ решается во втором приближении. После решения во втором приближении приращения напряжений определяется по выражению (3).