Компоненты напряжений рассчитываются после расчета деформаций

{}_n=[D]_n{}_n,{}_n– матрица столбец компонент напряжений _x,_y,_xy (плоское деформированное состояние)

[D]_n– матрица упругости или матрица упруго пластичности, зависит от того, в каком состоянии находится конечный элемент. Компоненты матрицы [D] также одинаковы для всех материальных точек конечного элемента вне зависимости от вида полинома (см. (1) правая часть) и при допущении однородности металла.

Вывод основной системы МКЭ.

1. Дискретизация области на конечные элементы.

2. Вывод функций форм и матриц дифференцирования конечных элементов.

3. Вывод основной системы мкэ и минимизация энергии деформации.

Разбиение области на элементы сводится к заданию числа, размеров и формы непересекающихся подобластей – конечных элементов.

Каждому конечному элементу соответствует группа узлов (вершин многоугольника для плоского конечного элемента, вершин многогранника для объемного конечного элемента). Всем узлам и элементам присваиваются порядковые номера. Для каждого узла указываются координаты. Вся эта информация обычно представляется в форме двух информационных файлов: файл координат и файл номеров узлов составляющих элементы.

В зависимости от размерности задачи плоскую или объемную область разбивают на: одномерные элементы; двухмерные элементы или трехмерные элементы.

Элементы, сторонами которых являются прямолинейные отрезки или гранями которых являются многоугольники, называют симплекс-элементами. В симплекс-элементе число узлов (вершин) всегда на единицу превышает размерность задачи.

При решении одномерной задачи применяют:

• одномерный симплекс-элемент с двумя узлами;

• одномерный квадратичный элемент с тремя узлами.

При решении двухмерных задач (плоское деформированное состояние, плоское напряженное состояние) применяют:

• треугольный симплекс-элемент с тремя узлами;

• прямоугольный симплекс-элемент с четырьмя узлами;

• квадратичный треугольный элемент с шестью узлами.

При решении трехмерных задач применяют:

• симплекс-элемент с четырьмя узлами – тетраэдр;

• симплекс-элемент с восемью узлами – параллелепипед.

При решении осесимметричных задач, применяют кольцевые конечные элементы, например с треугольным поперечным сечением.

При дискретизации области, необходимо стремиться к тому, чтобы отрезки, треугольники, тетраэдры приближались по форме к равным отрезкам, к равносторонним треугольникам, к правильным тетраэдрам. Такое разбиение обеспечивает более точные результаты, хорошо согласующиеся с экспериментальными данными.

В заключении отметим, что в областях резкого изменения (большого градиента) искомой характеристики Н.Д.С. следует проводить разбиение на мелкие по размерам элементы.

Каждой форме конечного элемента (отрезку, треугольнику и т.д.) соответствует (в смысле возможности определения коэффициентов полинома) интерполяционный полином, описывающий кусочно-непрерывную функцию перемещений (или приращений перемещений, или скоростей течения в зависимости от использующейся теории пластичности) внутри конечного элемента, т.е. полином с областью определения, ограниченной конечным элементом.

Полиномы соответствующие симплекс-элементам содержат константы и линейные члены, члены, содержащие независимые переменные x и y в первой степени.

Полином, соответствующий одномерному элементу имеет вид:

U_x,n=α₁+α₂·x,

двумерному треугольному симплекс-элементу:

U_x,n=α₁+α₂·x+α₃·y; (1)

U_y,n=β₁+β₂·x+β₃·y.

Количество коэффициентов в каждом полиноме равно количеству узлов конечного элемента.

Трёхмерному симплекс-элементу (тетраэдру):

U_x,n=α₁+α₂·x+α₃·y+α₄·z;

U_y,n=β₁+β₂·x+β₃·y+β₄·z;

U_z,n=c₁+c₂·x+c₃·y+c₄·z.

Методику вывода функций форм и матриц дифференцирования рассмотрим на примере треугольного конечного элемента.

Напомним, что функции формы, с применением которых удаётся выразить полиномы – кусочно-непрерывные функции (1) через узловые перемещения элемента: (будем говорить далее о перемещениях узлов, но всё остаётся в силе для приращений перемещений или скоростей узлов) содержатся в выражениях:

U_x,n=N_x,iq_x,i+N_x,jq_x,j+N_x,mq_x,m;

U_y,n=N_y,iq_y,i+N_y,jq_y,j+N_y,mq_y,m.

или в матричной форме:

{U}_n=[N]_n·{q}_n (2),

где {U}_n=;[N]_n=;

{q}_n=(см. рис.1.);

Y

q

y

,

m

q

x

,

m

m

q

q

y

,

i

q

y

,

j

q

x

,

j

j

i

n

.

x

,

i

X

Рис.1.

{U}_n – матрица-столбец полиномов n-го элемента,

[N]_n – матрица функций форм,

{q}_n – матрица-столбец перемещений узлов n-го элемента.

В зависимости (1) подставим значения перемещений в узлах и координаты узлов n-го элемента, получим в результате:

= ;

обозначим матрицу с размерами 6×6 -[c]_n, а матрицу-столбец коэффициентов- {α}_n, тогда:

{q}_n=[c]_n·{α}_n (3).

Из математики известно, что произведение матрицы на обратную матрицу к ней, равно единичной матрице:

[с]_n^-1[с]_n=[1].

Поэтому если левую и правую части (3) умножить слева на [с]^-1 то получим:

{α}_n=[c]^-1_n·{q}_n (3)

Зависимость (1) представим в виде:

{U}_n=[p]·{α}_n (4);

где [p]= - матрица, произведение которой на {α}_n равно исходным полиномам, принятым для описания кусочно-непрерывной функции с областью определения ограниченной конечным элементом.

Выражение (4) с учётом (3) принимает вид:

{U}_n=[p]·[с]^-1_n·{q}_n (5)

Сравнивая (2) с (5) заключаем что:

[N]_n=[p]·[с]^-1_n (6)

Обратная матрица [с]^-1рассчитывается следующим образом:

[с]^-1_n=;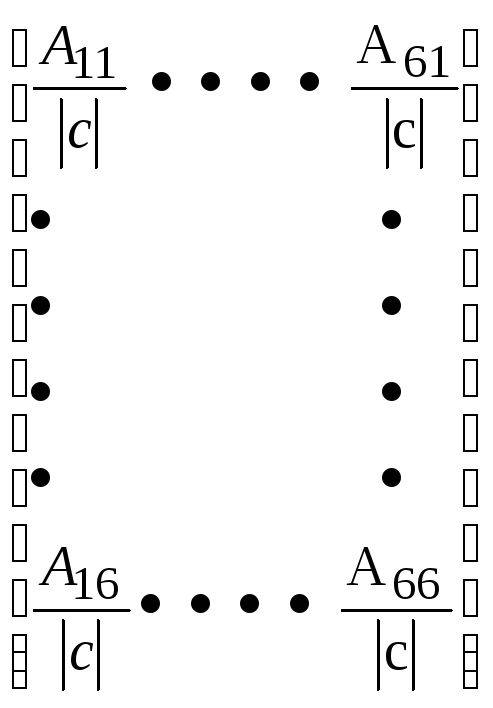

где А_i,j – алгебраическое дополнение элемента с_i,j;

|с| – определитель матрицы.

Алгебраическим дополнением элемента с_i,j называют определитель, составленный из элементов матрицы [c]_n оставшихся после вычеркивания в матрице i-ой строки и j-го столбца. При этом знак перед определителем +, если i=j, и – если i<>j.

Расчет по формуле (6) показывает что:

N_x,i =1/(2·Δ_n ) ·[(x_jy_m–x_my_j)+(y_j–y_m)·x+(x_m–x_j)·y];

N_x,j =1/(2·Δ_n )· [(x_my_i–x_iy_m)+(y_m–y_i)·x+(x_i–x_m)·y];

N_x,m =1/(2·Δ_n )· [(x_iy_j–x_jy_i)+(y_i–y_j)·x+(x_j– x_i)·y].

N_y,i=N_x,i;

N_y,j=N_x,j;

N_y,m=N_x,m;

Δ_n=1/2· – площадь n-го элемента.

Компоненты матрицы дифференцирования [В]_n получаются дифференцированием кусочно-непрерывных функций записанных в виде (2). Дифференцирование производится в соответствии с геометрическими соотношениями (и т.д.):

[В]_n=;

или если воспользоваться зависимостями (6):

[В]_n=1/(2·Δ_n)·– матрица дифференцирования для треугольного конечного элемента с узлами i,j,m.

Для вывода основной системы МКЭ [k]·{q}={F} используется принцип минимума энергии деформации.

Согласно методу баланса работ:

А_пл.д.=А_вн; (7)

где А_пл.д. – работа или энергия пластической деформации;

А_вн – работа внешних сил.

Составим из (7) энергетический функционал и выясним, при каких перемещениях узлов конечных элементов этот функционал принимает наименьшее значение.

Функционал: Ф= А_пл.д.–А_вн (8)

А_пл.д.=; (9)

Выражение (9) записано для случая плоского деформированного состояния заготовки с объемом очага пластической деформации V.

При конечно-элементном представлении тела интеграл (9) можно вычислить иначе:

А_пл.д.=

или _,

где k количество конечных элементов. С учётом зависимостей, по которым в рамках МКЭ рассчитываются {Е}_i и {σ}_i (компоненты деформаций и напряжений элемента) получаем:

; (10)

где k – количество конечных элементов;

; (11)

где m – количество граничных нагружаемых узлов;

q_j – перемещение j-го узла;

F_j – сила действующая на j-й узел.

Подставляя (10) и (11) в (8) получаем

; (12)

Из курса математики известно, что для отыскания минимального значения функционала берут производную или производные по переменным, от которых зависит функционал (Ф), приравнивают их 0, с последующим решением полученных уравнений относительно переменных. После расчёта переменных (корней системы) можно рассчитать минимальное значение Ф.

Переменными в функционале (12) являются перемещения (или приращения перемещений) всех узлов. Поэтому для расчета перемещений узлов возьмём частные производные по перемещениям всех узлов, приравняем их 0 и решим полученную систему относительно их.

Заметим, что каждая производная будет зависеть от перемещений узлов, т. к. в выражении (10) энергия элемента выражается через произведение матриц {q}^T_i и {q}_i, каждое уравнение будет иметь вид:

или , (13)

где [k]_i=[B]^T·[D]_i·[B]_I·V_i - матрица жёсткости i-го конечного элемента, одного из l элементов соприкасающимся в j–ом узле, - количество конечных элементов соседствующих вj-ом узле.

Уравнение равновесия j-го узла вида (13) можно записать в виде произведения матрицы-строки коэффициентов и матрицы-столбца перемещений соответствующим не отдельным элементам, а всей конечно-элементной сетке:

[k]_(2·j-1),m·{q}={F}_2·j-1,

для случая, если уравнение равновесия составлено для сил направленных вдоль ОХ,

[k]_2j,m·{q}={F}_2j – для сил направленных вдоль оси OY,

переменная m (если решается плоская задача) удовлетворяет неравенству: 1<=m<=(2·z), z-количество узлов,

{q}=

{F}_2j-1 и {F}_2j – компоненты матрицы-столбца нагрузки в (2j-1)-ой и (2j)-ой строках.

Ненулевые компоненты строк ( [k]_(2·j-1),m [k]_2j,m ) рассчитываются путём сложения соответствующих компонент матриц жёсткости [k]_i=[B]^T·[D]_i·[B]_I·V_i элементов, окружающих j-ый узел.

Формирование матрицы жесткости ([к ] ) – матрицы коэффициентов системы уравнений [K]*{Q}={F}.

1.Формирование матрицы жесткости способом объединения по узлам.

2. Формирование матрицы жесткости способом объединения по элементам.

Каждое уравнение системы [K]*{q}={F} является уравнением равновесия (без учета инерционных сил) соответствующего узла в направлении оси OX, OY или OZ. В каждом уравнении, в левой части, сумма проекций всех внутренних сил, действующих на узел в направлении оси OX или OY или OZ. Внутренние силы действуют на узел со стороны соседствующих в узле элементов (см. рис 1).

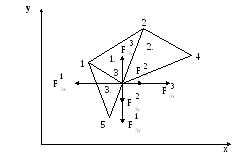
Рис. 1.

Внутренние силы выражаются через неизвестные узловые перемещения:

где [К]_е=1… - матрицы жесткости элементов с номерами 1, 2, 3;

- сила, действующая в направлении оси ОХ на i-ый узел со стороны j-го элемента;

- сила, действующая в направлении оси ОY на i-ый узел со стороны j-го элемента.

Пусть:

Составим сумму внутренних сил, действующих на третий узел в направлении оси ОХ:

Вектор строка:

[46 46 32 32 66 66 20 20 34 34] (1)

– представляет собой одну из строк матрицы жесткости [К], К_5,j – значения компонент этой строки получены присвоением значениям соответствующих компонентов матриц жесткости окружающих элементов или их сложением (сложением коэффициентов при одинаковых q).

Каждую компоненту матрицы жесткости [K] можно рассчитать по формуле:

,

где l – число окружающих узел элементов;

- компонента матрицы жесткости е-го элемента.

Процедура формирования матрицы [К] способом объединения по узлам:

Procedure Rachet_matrSt;

Var m1, m2, m3, m4, m5, m6: byte;

Begin

for i:=1 to 2*col_uzlov do

for j:=1 to 2*col_uzlov do st[i]^[j]:=0;

for n:=1 to kol_uzlov do

begin

for k:=1 to 9 do

begin

L:=uzel_elem[n,k];

if l>0 then begin

m1:=nod[L,1]*2-1;m2:=nod[L,1]*2;

m3:=nod[L,2]*2-1;m4:=nod[L,2]*2;

m5:=nod[L,3]*2-1;m6:=nod[L,3]*2;

if n=nod[L,1] then begin

st[2*n-1, m1]:=st[2*n-1, m1]+ste[L, 1, 1];

st[2*n, m1]:=st[2*n, m1]+ste[L, 2, 1];

st[2*n-1, m2]:=st[2*n-1, m2]+ste[L, 1, 2];

………………………………………………*8раз

st[2*n, m6]:=st[2*n, m6]+ste[L, 2, 6];

end;

if n=nod[L,2] then begin

st[2*n-1, m1]:=st[2*n-1, m1]+ste[L, 3, 1];

st[2*n, m1]:=st[2*n, m1]+ste[L, 4, 1];

st[2*n-1, m2]:=st[2*n-1, m2]+ste[L, 3, 2];

………………………………………………*8раз

st[2*n, m6]:=st[2*n, m6]+ste[L, 4, 6];

end;

if n=nod[L,3] then begin

st[2*n-1, m1]:=st[2*n-1, m1]+ste[L, 5, 1];

st[2*n, m1]:=st[2*n, m1]+ste[L, 6, 1];

st[2*n-1, m2]:=st[2*n-1, m2]+ste[L, 5, 2];

………………………………………………*8раз

st[2*n, m6]:=st[2*n, m6]+ste[L, 6, 6];

end;end;end;end;end;

Формирование матрицы жесткости способом объединения по элементам заключается в построении расширенных матриц жесткости с последующим их сложением.

Расширенная матрица жесткости элемента [K]_i,p строится из матрицы жесткости [K]_i конечного элемента.

Ненулевые компоненты матрицы [K]_i,р равны компонентам [K]_i, причем положение каждой компоненты матрицы [K]_i в матрице [K]_i,р определяется по номерам узлов составляющих i-й элемент (см. рис. 2).

в 2*1-1 ую строку

в 2*1 ую строку

в 2*3-1 ую строку

в 2*3 ую строку

в 2*2-1 ую строку

в 2*2 ую строку

Рис. 2. Схема к построению расширенной матрицы жесткости