10. О надежности моделирования строительных конструкций.

Известно, что при испытаниях конструкций для оценки их прочности, жесткости и устойчивости по результатам измерений параметров (перемещений, деформаций, нагрузок и т.д.) получают информацию в виде средних значений, дисперсий, коэффициентов вариации и других числовых характеристик случайных величин. При моделировании конструкций с учетом изменчивости параметров задача усложняется тем, что модель характеризуется случайными величинами, и результаты измерений подвергнуты изменчивости. Оригинал также определяется параметрами случайного характера (модулем упругости, пределом текучести или прочности материала, нагрузкой, геометрией и т.д.).

Следовательно, результаты расчетов оригинала характеризуются случайными величинами.

Проблема заключается в том, чтобы объективно оценить результаты анализа несущей способности и надежности оригинала по статистической информации обоих объектов. Например, сколько необходимо моделей для проведения испытаний, как сформировать критерии подобия, как оценить значение ошибки в окончательных результатах и т.д. Все это приводит к тому, что модель усиливает случайность, присущую оригиналу.

Если ранее использовались масштабы подобия, как отношения детерминированных величин, например, , и т.д. то в условиях их случайного поведения такие операции (деления) не применимы. В связи с этим в «статистическом» моделировании вводятся константы подобия [4] в виде , где - среднее значение параметра оригинала , - то же самое для модели . Для обеспечения подобия плотностей распределения и переходят к новым (безразмерным) параметрам в виде , , . В этом случае среднее значение .

Кроме того, каждый множитель преобразования должен удовлетворять требованию 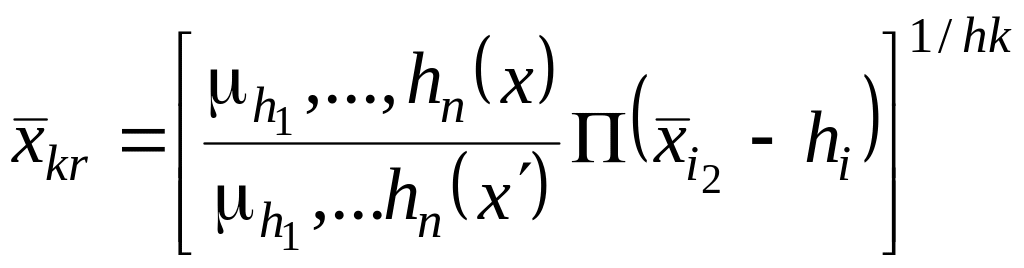, , - центральный смешанный момент.

При «статистическом» моделировании удается оценить точность результатов, получаемых на моделях: оценить адекватность расчетных и реальных моделей; определить область применимости детерминистического моделирования и решить другие задачи моделирования.

Наиболее простое, но менее точное, решение можно получить, если ограничиться лишь минимальной формой подобия в статистическом смысле, а именно, подобием первого порядка. Для этого нужно знать средние значения свойств модели и оригинала, которые определяют их поведение (свойства материалов, геометрии и нагрузки). Такое решение на практике возможно в том случае, когда коэффициенты вариации статистических характеристик свойств модели невелики (не более 0,12-0,15) [4]. Во-вторых, если можно ограничиться одним экземпляром модели и если для практики погрешность результатов в (10-20)% является приемлемой.

Для решения задачи вводится индикатор подобия, в частности

при , , где - соответственно множители преобразования для сосредоточенной силы , модуля упругости , геометрических размеров , напряжений и перемещений .

Аналогично детерминистическому подходу переход от одной величины модели к оригиналу выполняется с помощью констант подобия в виде

, ,

где , - средние значения величины модели и оригинала, - константа подобия, содержащая погрешность при заданной вероятности подобия .

В результате того, что , определенный на моделях имеет интервал, определяемый вероятностью и значениями измерений, то и будет характеризоваться интервалом.

Однако для усвоения теории статистического моделирования требуются знания, выходящие за рамки существующих учебных планов и программ специальностей 270102 и 270105 то, в связи с этим, мы ограничиваемся только этими замечаниями, а для подтверждения этого и иллюстрации расчетов приведем один пример на моделирование строительной конструкции заимствованный из [4].

ПРИМЕР ОЦЕНКИ ТОЧНОСТИ РЕЗУЛЬТАТОВ И ПЛАНИРОВАНИЯ ИСПЫТАНИЙ НА МОДЕЛЯХ

Оценка точности результатов, полученных на упругой модели структуры, изготовленной из одного материала.

Модель структуры изготовлена в масштабе 1/70. Нагружение модели осуществлялось сосредоточенными грузами по . Материал модели – полистирол. Модуль упругости полистирола для модели определялся на семи образцах, по результатам испытаний которых можно найти ; ; Других статистических данных в работе не имеется.

Деформации в элементах «структуры» определялись в предположении линейного напряженного состояния в упругой области. Условие подобия в этом случае выражается одним индикатором подобия через средние значения

(1)

при , , где и - соответственно множители преобразования для сосредоточенных нагрузок, модуля упругости, геометрических размеров, напряжений и перемещений.

Учитывая, что и , индикатор подобия (1) можно записать, используя значения и .

Интервальная оценка для напряжений и перемещений в оригинале, подобном данном модели, будет иметь вид:

; (2)

(3).

В индикатор(1) входят значения нагрузок, модуля упругости, геометрических размеров. Ввиду отсутствия данных полагает, что при условиях эксперимента коэффициенты вариации , .

Модуль упругости определен на семи образцах, его значение случайно. Пусть квантиль . По табл. при квантиль . При

, - коэффициент Стьюдента

получаем относительные погрешности , .

Возможная погрешность в оценке равна: . Наибольшее значение коэффициента вариации .

Среднее квадратичное отклонение индикаторов при и ( - число оригиналов, - число моделей) будет

.

Предположим, что плотности распределения и нормальны, тогда эксцесса , надежность (вероятность)

или погрешность

.

Здесь - обратная функция Лапласа.

Приняв по таблицам функции Лапласа легко найти .

Отсюда по (2) можно установить интервалы для (напряжение в натуральной конструкции)

,

а по формуле (3) найдем интервал для (перемещения)

.

Приняв найденные значения и в качестве математических ожиданий можно найти с риском ошибки 5%, что погрешность в оценке напряжений не превышает +22% и -39%, а в оценке перемещений +11,5% и -18%.

Более высокий уровень вероятности здесь не был бы оправдан, учитывая, что моделирование в данном случае проводилось с целью проверки метода расчета.