5. Критерии подобия

Необходимым и достаточным признаком физического подобия двух явлений является равенство численных значений независимых безразмерных комбинаций из основных параметров для рассматриваемых систем.

Независимые безразмерные комплексы в этом случае называют критериями подобия.

В примере с такими критериями подобия будут следующие безразмерные комплексы .

Особенностью этих критериев является то, что значения их для модели и натуральной конструкции одинаковы. Для обозначения одинаковости применяется символ ( - «одно и то же» в переводе с латинского).

Итак, , , , , или в развернутой форме для натуральной конструкции, обозначаемой 1 и для модели, обозначаемой 2 можно записать , , , , , (2)

Из (2) видно, что критерии подобия в виде безразмерных комплексов одинаковы (подобны) для натуральной конструкции и ее модели.

В зависимости от поставленной задачи используются различные критерии подобия. Наиболее простыми являются задачи на механическое подобие в упругом состоянии. Эти задачи и будут рассматриваться ниже. Усвоив их решение, можно переходить к упругопластическим, физическим и другим более сложным задачам моделирования.

6. Масштабы подобия

Основным вопросом при разработке механических моделей является выбор масштабов моделирования. Обычно начинают с выбора геометрического масштаба, обозначаемого (индекс 1 относится к натуре, 2 - к модели). Затем выбирают материал для модели и находят масштаб модуля упругости и коэффициента Пуассона . Материалы для натуры и модели заранее известны, т.е. известны и . При этом имеем в виду, что масштабы площадей , объемов , моментов инерции и т. д. определяются через масштаб длин .

Масштабы безразмерных комбинаций комплексов принимаются равными единице, т. е. , и т.д. Если обозначить , то . Отсюда видно, что напряжение в натуральной конструкции можно найти простым умножением напряжения , найденного экспериментально в модели в сходственной точке, на масштаб напряжений. Таким же образом находятся и другие искомые параметры натуральной конструкции , и т. д. Масштаб находится после того, как будет найдено , а масштаб из после того, как будут найдены и .

7. Техника моделирования

Разберем технику моделирования на простейших примерах на основе так называемой классической теории подобия.

Пример 1. Дана балка (рис. 4), изготовленная из бетона марки М200 и загруженная в середине пролета силой . Модуль упругости материала . Длина балки . Сечение прямоугольное , . Требуется найти , , и в середине пролета балки по результатам испытаний ее модели. Модель изготовлена из бетона той же марки . Длина балки-модели принята .

.

Основные параметры . Отсюда находим , , .

Безразмерные комплексы: .

Масштабы: , ; ; ; .

Натуральная

балка

Модель

Рис. 4

Найдем для модели значения .

Из геометрического подобия найдем и . Можно иначе. Известно, что безмерные комплексы в масштабах всегда равны единице. Тогда из найдем . Из найдем и т.д.

Изготовим и проведем испытания модели. В результате испытаний и измерений на модели значений , и получили , , .

После этого найдем искомые параметры в балке-натуре.

; ; .

Аналитическая проверка значений показала их совпадение с экспериментальными результатами. Пример заимствован из [3].

Пример 2. Консольная балка представлена на рис. 5.

Образец № 1 - «натура» выполнен из углеродистой стали С45. Характеристики образца № 1: , , , .

Образец №2 - «модель» выполнен из алюминиевого сплава Д16Т. Характеристики образца № 2: , , , . Требуется по результатам испытаний образца № 2 найти прогиб конца балки образца № 1.

Основные параметры в примере .

Рис. 5.

В качестве безразмерных комплексов (комбинаций) примем и . Найдем масштабы .

Так как , то . Из ; , следовательно , отсюда .

Отсюда из найдем или . Будем задаваться значением , находить , прикладывать к модели (образец №2), находить измерениями прогиб и с помощью масштаба находить .

Все результаты сведены в табл. 1

Таблица 1

Результаты испытаний и измерений модели и переноса значений на образец № 1 путем простого перемножения на масштаб

123	10,7	0,0975	0,195	0,195	0,065
245	21,3	0,1955	0,391	0,391	0,125
368	32,0	0,2930	0,586	0,586	0,187
490	42,7	0,3900	0,780	0,780	0,250
613	53,4	0,4875	0,975	0,975	0,312
735	64,0	0,5860	1,172	1,172	0,375

Пример 2 заимствован из [1].

Пример 3. Иногда модель может быть больше натуральной конструкции. Рассмотрим предыдущий пример в предположении, что образец № 1 становится моделью, а образец № 2 натуральной конструкцией.

Найдем масштабы, приняв образец № 2 натурой с индексами 1, а образец № 1 - моделью с индексом 2.

, т.к. , то ;

.

Из ;

.

Будем задаваться значением и находить .

Нагружаем модель нагрузкой и измеряем . Значение . Сведем все результаты измерений и расчетов в табл. 2.

Таблица 2

Результаты испытаний модели и вычисления прогиба

49	570	0,90	0,45	0,200	0,280
98	1140	1,80	0,90	1,800	0,570
147	1710	2,70	1,35	2,700	0,840
32	368	0,58	0,26	0,580	0,162
10,7	123	0,17	0,09	0,180	0,0570

Построим графики зависимости в критериальной форме для обоих случаев моделирования по примерам 2 и 3.

График представлен на рис. 6.

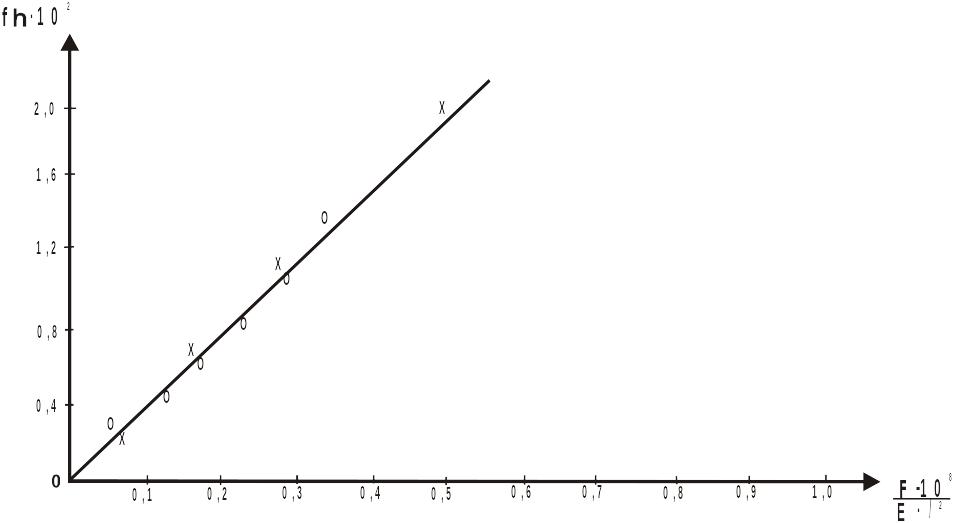
Рис. 6

- экспериментальные точки по примеру 2,

- то же самое по примеру 3.

Из графика видно, что экспериментальные точки лежат на одной прямой. Значит, модели и натуральные конструкции оказались подобными.

Пример 4. Для представленной на рис. 7 балки требуется найти и с помощью испытания ее модели. Исходные данные о балке: , , (сталь), сечение прямоугольное , .

Сведения о модели: , (сталь).

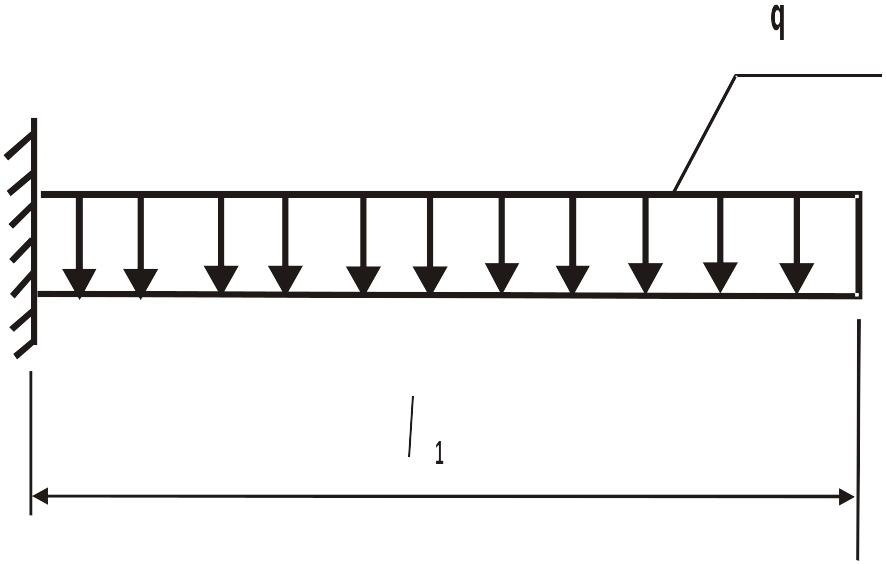
Рис. 7

Основные параметры: .

, , . Принимаем в качестве безразмерных комплексов ; ; .

Масштабы ; ; , , , отсюда , , .

Найдем из , ,

отсюда .

После изготовления модели ее испытывают и находят значения и .

отсюда при ,

.

Проверим теоретическими расчетами:

,

;

, .

Пример 5. По условию предыдущего примера, но при действии не нагрузки , а внешнего момента , приложенного к свободному концу балки, и исходным данным, принятым из табл. 7.3, требуется найти и в натуральной балке с помощью испытаний ее модели. Найдите значение момента для модели, если для балки его значение (см. табл. 3), а также размеры балки-модели . Масштаб момента обозначьте . Составьте безразмерные комплексы и . Определите теоретическое значение и для балки и теоретичное значение и для модели от действия и . Проверь равенства и .

Таблица 3

Исходные данные для решения примера 5 студентами-заочниками

Последняя цифра шифра студента					Предпоследняя цифра шифра студента
1 2 3 4 5 6 7 8 9 0	2 3 4 5 6 7 8 5 4 3	1 1 1 2 2 2 2 1 2 1	6 8 10 10 12 12 12 8 6 6	3 4 5 6 6 5 5 4 4 3	1 2 3 4 5 6 7 8 9 0	30 40 60 60 40 40 20 80 80 60

, .

Пример 6. Рассмотрим более сложную задачу из [1]. С целью выявления влияния размеров и жесткости площадки на сферическом куполе здания на величину критической нагрузки , где - критическое значение внешнего давления на оболочку купола. Были изготовлены и испытаны модели купола. Схема оболочки и площадки на ней представлены на рис. 8.

Рис. 8

В качестве определяющих параметров включены все независимые линейные размеры купола - (см. рис. 7.5). В число основных определяющих) параметров вошли такие свойства материала (сталь) и . В качестве определяемого параметра принята критическая нагрузка .

Список основных параметров: ; , .

Безразмерные комплексы (критерии подобия).

.

Были изготовлены модели с различным безразмерным отношением . При этом некоторые критерии подобия сохраняли постоянное значение . Значения изменялись при каждой модели в зависимости от критерия . В процессе нагружения моделей оболочки нагрузкой происходило ее прощел-кивание, что свидетельствовало о достижений критического значения нагрузки , а точнее критического значения безразмерного параметра .

Результаты испытаний моделей представлены в табл. 4 и на рис. 9.

Таблица 4

Экспериментальные значения верхней критической нагрузки для серии моделей полого сферического купола

№ модели
1 2 3 4 5 6	1,50 1,50 2,00 2,50 1,00 1,00	600 600 900 1360 500 510	0,115 0,115 1,154 1,197 0,077 0,077	1,81 1,81 2,70 4,00 1,50 1,52

На рис. 9 представлена кривая функциональной зависимости .

Рис. 9

При значениях меньше 0,07 прощелкивания не наблюдалось (не наблюдалось потери устойчивости), и разрушения происходили из-за деформации купола под плитой. Из рис. 9 видно, что с ростом отношения значение возрастает.

Аппроксимируя кривую аналитической функцией можно определить значения , в зависимости от и при других постоянных (неизменных) параметрах оболочки.

Пример 6. Иногда для испытаний приходится изготавливать несколько образцов-моделей для того, чтобы выяснить поведение натуральной конструкции при изменении ее параметров. Также изготавливается и испытывается несколько образцов-моделей, когда хотят учесть случайный характер некоторых параметров, когда устанавливается надежность моделирования [4].

Рассмотрим особенность моделирования и испытания моделей в заклепочном соединении двух листов при их центральном растяжении [1]. Конструкция соединения показана на рис. 10.

Прочность соединения зависит от механических свойств материалов в соединении и от размеров деталей соединения. К их числу относятся предел прочности листов , модуль упругости , размеры . Примем, что и , как разрешается по нормам конструирования соединений.

Материалы натуральной конструкции - сталь, материалы модели - алюминиевый сплав.

Рис. 10

Целью эксперимента является определение несущей способности заклепочного шва при разрушении стыка по одной из причин:

1) вследствие вырыва листа под заклепкой; 2) из-за смятия материала листа;

3) из-за среза заклепки.

- искомое разрушающее напряжение в ослабленном отверстиями сечении листа.

Ряд несущественных факторов, влияющих на прочность соединения, учитывать не будем. Например, влияние сил трения между листами и накладками и др.

За основные параметры примем . Вместо шага введем коэффициент ослабления листов ( - число заклепок в ряду). Тогда будем иметь параметры . По -теореме .

В качестве безразмерных комплексов примем ; ; ( - безразмерный параметр).

При изготовлении опытных образцов (моделей) будем изменять размеры , изменяя тем самым параметры и . Тогда будем находить - в виде функциональной зависимости .

Результаты испытаний по нескольким образцам-моделям представлены на рис. 11 в виде графика, построенного при фиксированных значениях .

Из графика рис. 11 видно, что при одном и том же значении прочности материала листов несущая способность соединения с ростом (с уменьшением , т.е. или числа заклепок, или их диаметра) сначала возрастает до , а затем резко снижается.

Рис. 11

Если бы произвести теоретические расчеты натуральной конструкции по разрыву листа в ослабленном сечении, то в тех же осях координат получили бы прямую 1 на рис. 11, при расчете по смятию материала листа - прямую 2 и при расчете по срезу заклепки - прямую 3.

Аналогичные испытания можно провести с болтовым и другим соединением листов.