Введение

Метод моделирования является одним из средств экспериментального исследования конструкций на прочность, жесткость и устойчивость. С помощью этого метода можно исследования конструкции (натуры) заменить исследованием ее модели, меньшей по размеру и выполненной практически из различных материалов. По исследованным параметрам, например, напряжениям, прогибам и т.д., модели можно перейти к сходственным параметрам (напряжениям, прогибам и т. д.) натуральной конструкции. Все это позволяет снизить затраты на проведение испытаний натуральной конструкции, выполнить их с большей точностью (в лабораторных условиях) и сократить сроки проектирования и испытаний конструкции.

Особое значение приобретает моделирование, когда возникают сомнения в правдоподобии теоретического расчета или когда его совсем нет.

В настоящих методических указаниях разбираются кратко основные положения в методике моделирования и приводятся примеры на механическое моделирование применительно к строительным специальностям. Приведены примеры для самостоятельной работы студентов. В качестве примера постановки самой задачи сформулируем следующую проблему. Имеется деревянная балка (в натуре или пока в проекте) со всеми геометрическими и механическими характеристиками. Известна нагрузка F и способ передачи ее, как показано на рис. 1, в натуральной балке.

Рис. 1

При этих данных требуется определить, насколько она прогнется, например, в середине пролета , и какие при этом возникнут по значению, например, нормальные максимальные напряжения в балке. Для этого необходимо заменить ее моделью, в общем виде представленной на рис. 2, и при ее испытании найти ответы на поставленные вопросы. При этом значения и др. известны, также известен материал натуральной балки и его физико-механические характеристики (модуль упругости, предел прочности и т.д.), а вот значения и т.д. неизвестны и их предварительно (до изготовления модели) необходимо найти методами теории подобия, а некоторыми параметрами задаются ( и др.).

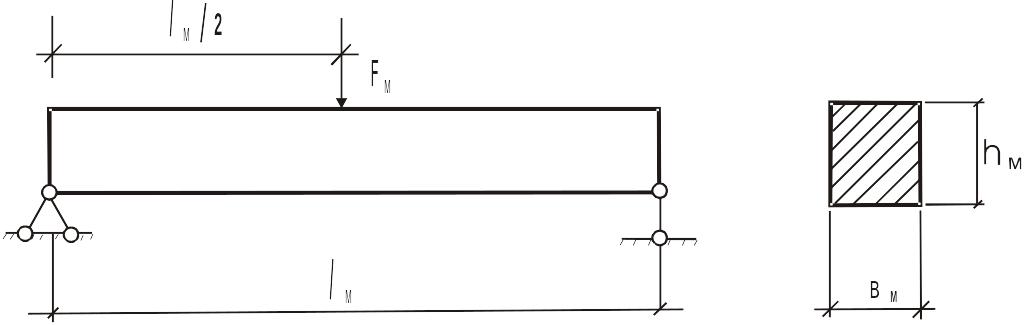
Рис. 2

Студентами заочной формы обучения в контрольную работу по дисциплине входит решение примера 5 настоящих методических указаний.

1. Формула размерностей, матрица размерностей. Ранг матрицы.

Прежде чем решать поставленную задачу во «Введении» придется рассмотреть некоторые теоретические вопросы.

В настоящее время в соответствии со стандартом СТСЭВ 1052-78 принята система СИ единиц измерения: - масса, - длина, - время. Физическая (размерная) величина характеризуется определенной размерностью. Обозначим слово размерность символом (от французского слова - размерность) [1].

Например, размерность скорости.

размерность в основных единицах системы СИ силы.

В качестве основных единиц измерения системы СИ приняты единица длины , единица массы и единица времени . Тогда в принятых обозначениях ( ) можно записать

, .

В общем случае для любой физической величины и называется она формулой размерностей. Так , . Для совокупности параметров ( - напряжение, - длина, - сила, - модуль упругости, - коэффициент Пуассона) можно составить матрицу размерностей в виде:

	-1	1	1	-1	0
	1	0	1	1	0
	-2	0	-2	-2	0

или в виде общепринятого обозначения матрицы

(1)

Известно, что определители, составленные из элементов пересекающихся строк и столбцов матрицы называются минорами матрицы. Рангом матрицы (1) называется наивысший порядок отличных от нуля миноров этой матрицы [1]. Например, перебрав все возможные определители-миноры матрицы (1), можно установить, что лишь определители 2^го порядка или , или и др. не равны нулю, а определители 3^го порядка равны нулю. Значит, ранг матрицы (1) равен 2. Это усвоить важно для применения нижеописанной -теоремы.

Примечание. Для уменьшения объема работы по определению ранга матрицы (1) для безразмерных величин (в нашем случае ) соответствующий столбец матрицы (1) исключается.