7.2 Експериментальні дослідження

7.2.1 Опис лабораторної установки

Функціональна схема установки зображена на рис. 7.2. Трифілярний підвіс становить собою диск Д, підвішений на трьох нитках, закріплених

симетрично у верховинах рівнобічного трикутника, що вписаний в шайбу Ш. На диск кладуть тіло, момент інерції якого необхідно визначити.

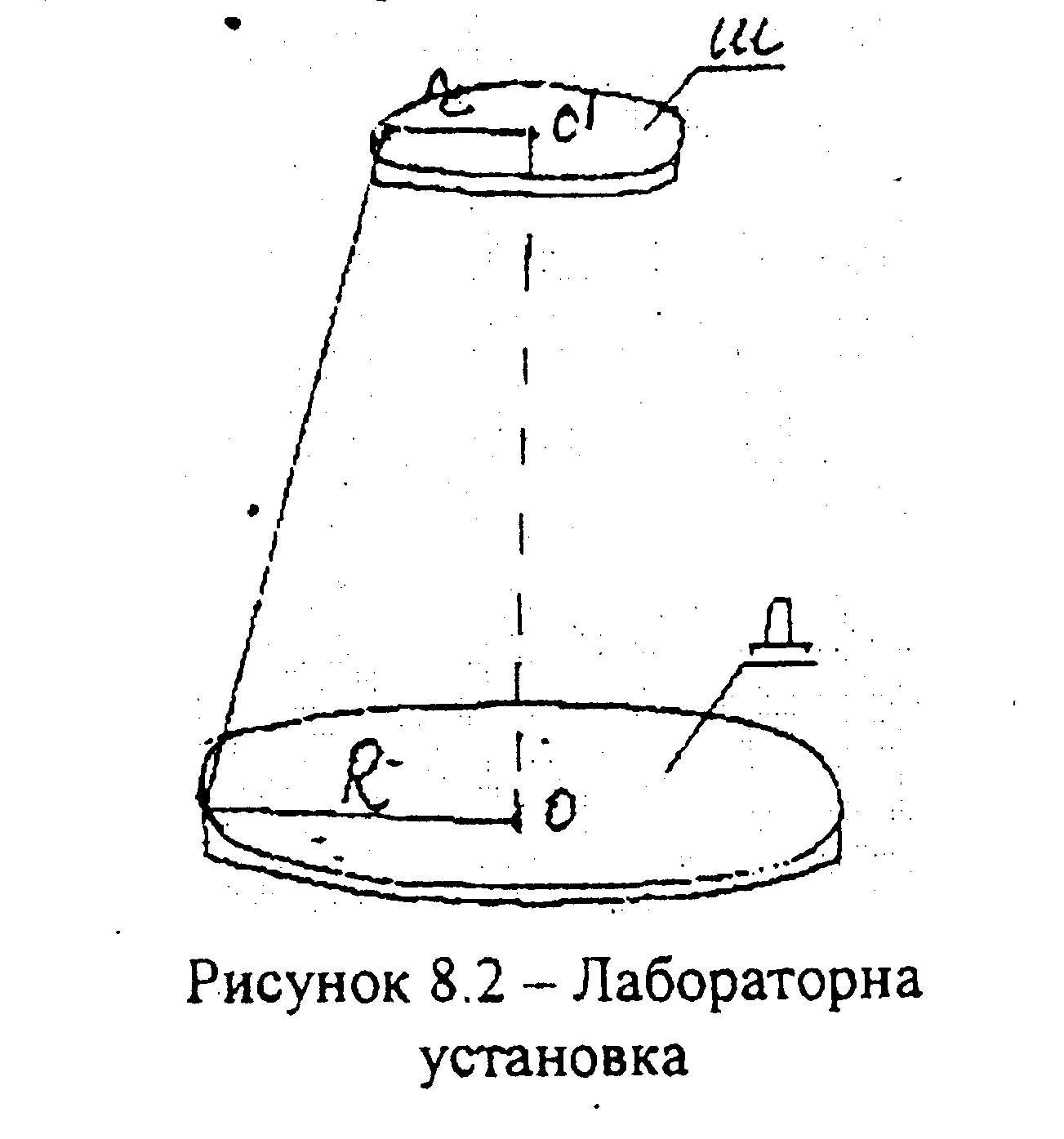
Рисунок 7.2 –Лабораторна установка.

7.2.2 Порядок виконання роботи

1. Заміряти довжину ниток L.

2. Визначити масу (m_τ), тіла що заміряється зважуванням.

3. Заміряти секундоміром час t 25-50 коливань диска. Повторити заміри 4-5 разів.

4. Тіло, що досліджується, помістити на диск, сумістивши вісь тіла, відносно якої визначається момент інерції, з віссю приладу.

5. Заміряти секундоміром час t₁ 25-50 коливань диска з тілом. Повторити заміри 4-5 разів.

Знайти період коливань Т₁ навантаженого приладу.

6. За формулою (7.14) обчислити момент інерції I_τ тіла.

7.3 Обробка результатів вимірювань

1 Обчислити середні значення прямих вимірювань: L, m, t, t₁

2 Обчислити похибки прямих вимірювань: : ΔL, Δm, Δt, Δt₁

3 Обчислити середні значення непрямих вимірювань: T, T₁, I_τ.

4 Обчислити похибки непрямих вимірювань: ΔT, ΔT₁, ΔI_τ.

7.4 Зміст звіту

Зміст повинен мати: таблицю вимірювання величин і розрахунок моментуінерції тіла, вивід формули відносної похибки моменту інерції з формули (7.14) і розрахунок відносної похибки з одержаної формули.

7.5 Контрольні запитання

1. Що називається моментом інерції матеріальної точки, тіла?

2. Які властивості тіла характеризує момент інерції?

3. Який коливальний рух називається гармонічним?

4. За якою формулою можна розрахувати кінетичну енергію тіла, що обертається?

5. Як записати закон збереження енергії крутильних коливань диска?

6. Чому необхідно, щоб центр тіла знаходився на одній вертикальній осі з центром інерції диска?

7. Які закони збереження виконуються при крутильних коливаннях? Сформулюйте їх.

8 Дослідження закону збереження енергії і визначення моменту інерції тіла за допомогою маятника Максвелла

Мета роботи: визначення моменту інерції тіл, що обертаються.

8.1 Теоретичні дослідження

Маятник Максвелла – це диск, закріплений на осі і підвішений за біфілярним способом за допомогою двох ниток до нерухомого кронштейну.

Розглянемо фізичні особливості руху маятника Максвелла.

На маятник, що знаходиться на підвісі, діють дві сили - тяжіння тg та натягу нитки Т (рис. 8.1). Миттєвою віссю обертання маятника є лінія, що проходить через точку 0₁ і перпендикулярна площині маятника (швидкості точок, розташованих на цій лінії, дорівнюють нулю).

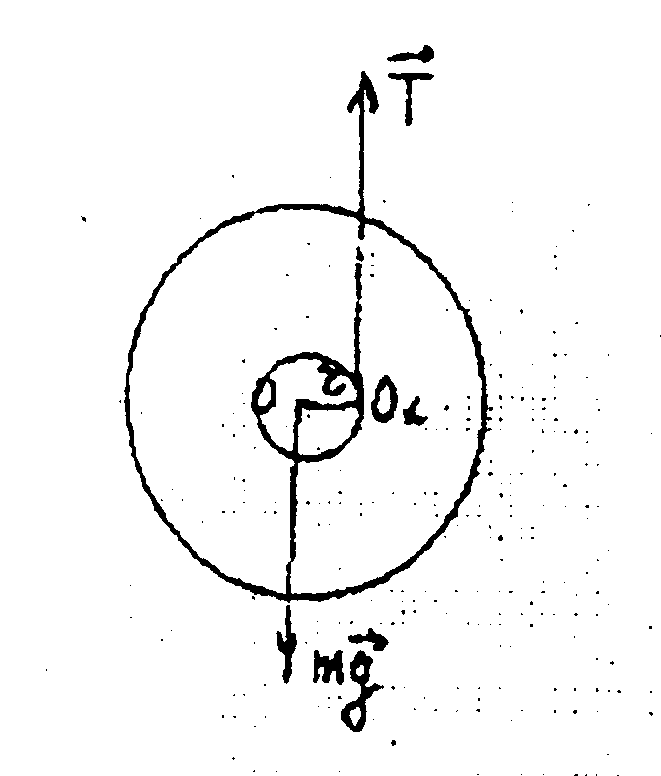
Рисунок 8.1 Фізична модель досліду.

Запишемо рівняння динаміки обертального руху:

М = І , (8.1)

де М - момент сили тяжіння відносно осі обертання О₁;І - момент інерції маятника відносно тієї ж осі О₁. При цьому:

М = m·g·r (8.2)

та

ω=v/r , (8.3)

де r - радіус осі маятника, тобто відстань від центру мас до внутрішньої поверхні нитки підвісу; v - швидкість руху центру мас.

Момент сили натягу Т відносно осі 0₁ дорівнює нулю. Враховуючи що:

, (8.4)

де а- прискорення, з яким рухається вниз центр мас системи, і підставляючи рівняння (8.2) та (8.4) в (8.1), одержимо:

І = тgr²/а . (8.5)

Якщо маятник пройшов відстань h за час t, маючи в початковий момент руху нульову швидкість (ύ₀=0), то:

h=аt²/2 (8.6)

та

а=2h/t². (8.7)

Підставимо формулу (8.7) в (8.5):

I = mgr²t²/2h (8.8)

Зв’язок між моментом інерції маятника I відносно миттєвої осі O₁ і моментом інерції I_о відносно осі О, що проходить через центр мас, визначається теоремою Штейнера:

I = I_о+mr² (8.9)

Звідки, враховуючи (8.8), отримуємо:

, (8.10)