2.3 Експериментальні дослідження

2.3.1 Опис лабораторної установки

Функціональна схема прибору Атвуда показана на рис. 2.2:

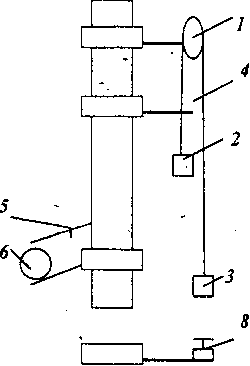
1-блок ; 2,3- вантажі; 4 - верхня платформа; 5- вимикач; 6- секундомір;

7-перевантаження; 8- платформа з автоматичним вимикачем секундоміра.

Рисунок 2.2- Лабораторна установка.

Через легкий блок перекинута нитка з вантажами. Якщо на вантаж 3

покласти перевантаження P_i (масою т_і), система почне рухатися з прискоренням. В момент удару вантажу по платформі 8 спрацьовує вимикач секундоміра.

3.3.2 Порядок виконання роботи

1. Установити платформу 4 (рис. 2.2.) на відстані h=1м від автоматичного вимикача 8. На вантаж 3 покласти перевантаження, попередньо зваживши його декілька разів і визначивши середнє значення маси.

2. Підвісити вантаж 3 з перевантаженням до верхньої платформи.

3. Опустити вантаж 3, водночас включивши секундомір.

4. Виміряти час падіння вантажу з перевантаженням 5 разів.

5. Додаючи до вантажу перевантаження, виконати пп. 2-6, а дані занести у таблицю.

4. Обробка результатів вимірювання

1. Обчислити значення прискорення для різних перевантажень.

2. Обчислити похибку у визначеннях а.

3. Побудувати графік залежності а(т_i g ).

4. За графіком визначити F_тер.

5. Знайти момент сили тертя за формулою:

N_тер = F_тер R. (2.8)

1. Зміст звіту

Звіт повинен містити: мету роботи; схему лабораторної установки; результати вимірів, зведені в таблицю; статистичну обробку результатів вимірювань; графік залежності прискорення від величини (m_i g); короткі висновки.

3.5 Контрольні питання і завдання.

1 Які прямі вимірювання необхідно виконати?

2. 3а якого формулою обчислюють прискорення у даній роботі?

3. Запишіть рівняння руху вантажів при наявності тертя?

4. Дайте визначення матеріальної точки абсолютно твердого тіла.

5. Викладіть способи завдання руху (векторний, координатний,

природний), швидкість і прискорення матеріальної точки при різних

способах завдання руху.

6 Прискорення при криволінійному русі (повне, нормальне,

тангенціальне).

7 Сформулюйте закони динаміки. Запишіть рівняння руху матеріальної

точки.

3 Дослідження закономірностей часткового пружного удару на. Прикладі взаємодії двох кульок

Мета роботи: визначення коефіцієнта відновлення швидкості та енергії дисипації при частково пружному зіткненні двох кульок.

3.1 Теоретичні дослідження

При виконанні лабораторної роботи слід знати, що у фізиці часто спостерігаються явища, зв'язані з взаємодією тіл, між якими діють потенційні сили. Взаємодія, в результаті якої змінюється стан руху тіл, називається ударом.

Рисунок 3.1- Фізична модель досліду

Звичайно, при ударі тіл потенціальною енергією нехтують - це дає змогу користуватися законами збереження механічної енергії у формі закону збереження кінетичної енергії. При частково пружному ударі металевої кульки об перешкоду частина кінетичної енергії переходить в енергію залишкової деформації. На підставі законів збереження енергії та імпульсу маємо:

mν₀² /2 = mν ²/2 + Е_д ; (3.1)

mν₀ = mν + ΔР, (3.2)

де Е_д - розсіяна енергія; m - маса кульки; ν₀ - швидкість кульки до удару; ν - швидкість кульки після удару; ΔР - зміна імпульсу кульки.

Для кількісної оцінки зменшення швидкості вводиться коефіцієнт відновлення

k = ν/ ν₀, (3.3)

Таким чином, для знаходження основних характеристик частково пружного удару, необхідно виміряти кути відхилення кульки перед і після ряду ударів.

При частково пружному зіткненні двох кульок, коли їх швидкості в момент удару рівні та після удару рівні одне одному за величиною та протилежні за напрямком, коефіцієнт відновлення можна визначити за формулою:

К = |u₂; - u₁| / |ν₁ - ν₂| , (3.4)

де | и | - швидкість кульки після удару, |u| =| u₂|=| u₁|;|ν| - швидкість кульки безпосередньо перед ударомν; |ν| = |ν₂|= | ν₁|

Враховуючи це, можна записати

К = |u|/ |ν| (3.4)

Коефіцієнт відновлення залежить тільки від матеріалу кульок, що зіткнулися. Величину К простіш за все визначити при центральному ударі кульок рівної маси.

Нехай, дві однакові кульки висять на нитках рівної довжини l (рис. 3.2). Якщо обидві кульки відхилити на однакові кути α₀ та відпустити, то їх швидкості в момент зіткнення будуть однакові. Неважко розрахувати величину цієї швидкості ν, враховуючи те, що потенціальна енергія піднятої на висоту h кульки, перейде в її кінетичну:

mgh = тv²/2. (3.5)

У даному досліді простіше вимірити не висоту підйому h, а кут α₀, на який була відхилена кулька. З рис.4.1 випливає, що:

h = l-lсos α₀ = 2lsіn² α₀ / 2 . (3.6)

Якщо кут відхилення кульок достатньо малий (кут вимірюється в радіанах 180⁰ =3,14 рад.), то можна прийняти:

sіп² α₀ /2 = (α₀ /2)². Тому h = 2l(α₀ /2)² . (3.7)

Враховуючи це, знайдемо ν із співвідношення (3.5):

, (3.8)

За аналогією можна визначити і швидкість кульок після зіткнення, виміривши величину кута α, на який відхилиться будь-яка з кульок після зіткнення, тобто:

(3.9)

Підставляючи значення (3.8) і (3.9) у співвідношення (3.4), знайдемо коефіцієнт відновлення швидкості через відповідні кути:

K = α_{i+1 /} α_i , (3.10)

де α_i+1 - кут відхилення після будь-якого зіткнення. Якщо α_i+1 дещо відрізняється від попереднього кута α_i, доцільно виміряти величину кута після кількох зіткнень (2-4). В цьому випадку формула для коефіцієнта відновлення зміниться.

Після першого зіткнення К= α₁/α₀;

другого К= α₂/α₁;

третього К= α₃/α₂;

після будь-якого n зіткнення К= α_n+1/α_n;

Перемноживши всі ці рівності, отримаємо:

Кⁿ= α₁ / α₀ * α₂ / α₁ * α₃ / α₂ *_…* α_n / α_n-1 = α_n / α₀;

Звідки, К = (3.11)

Таким чином, для знаходження основних характеристик частково пружного удару необхідно виміряти кути відхилення кульки перед і після ряду ударів.

Частково пружний удар супроводжується, як відомо, дисипацією (розсіянням) енергії: частка механічної енергії переходить в інші види енергії:енергію залишкової деформації і внутрішню (теплову) енергію. Енергію дисипації E_д одної кульки, відповідно одному зіткненню, можна виразити через коефіцієнт відновлення К. Для цього запишемо закон збереження енергії для двох однакових кульок:

mv₁²/2 + mv₂²/2 = mu₁²/2 + mu₂²/2 + 2Е_д (3.12)

Враховуючи що |v| = |v|₂ = |v₁ |, |u| = |и₂| = |u₁| , отримаємо

mv²/2 = ти²/2+2Е_д , звідки,

Е_д = тv²/2(I-и² / v²). (3.13)

Враховуючи (3.4) і (3.8), маємо

(3.14)