17 Дослідження явища взаємоіндукції

Мета роботи: дослідити явище взаємоіндукції, вивчити закон Фарадея, розглянути принцип роботи трансформатора та визначити його характеристики коефіцієнт трансформації напруги, коефіцієнти взаємоіндукції обмоток трансформатора та його ККД.

17.1 Теоретичні дослідження

13.2 Методичні вказівки з організації самостійної роботи студентів

Змінний струм, який протікає в одному з контурів (рис 13.1), наприклад в контурі 1, створює змінне магнітне поле, яке викликає появу ЕРС індукції в контурі 2. Таке явище називається взаємоіндукцією. ЕРС взаємоіндукції (як і самоіндукції) визначається за законом Фарадея:^-

(17.1)

де Ф - магнітний потік контуру зі струмом.

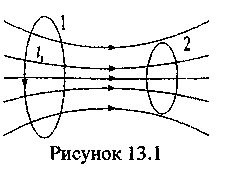
Рисунок 17.1 Явище взаємоіндукції.

На практиці звичайно магнітний потік створюється не одним витком, а

котушкою з великою кількістю витків. Повний магнітний потік крізь усі витки котушки, пропорційний кількості витків N та магнітному потоку одного витка Ф: Ψ = NФ. Величину Ψ іноді називають потокозчепленням. Щоб підсилити взаємодію між повними магнітними потоками котушок, останні потрібно розташувати навколо замкнутого феромагнітного осердя (рис. 17.2). Такий пристрій є трансформатором.

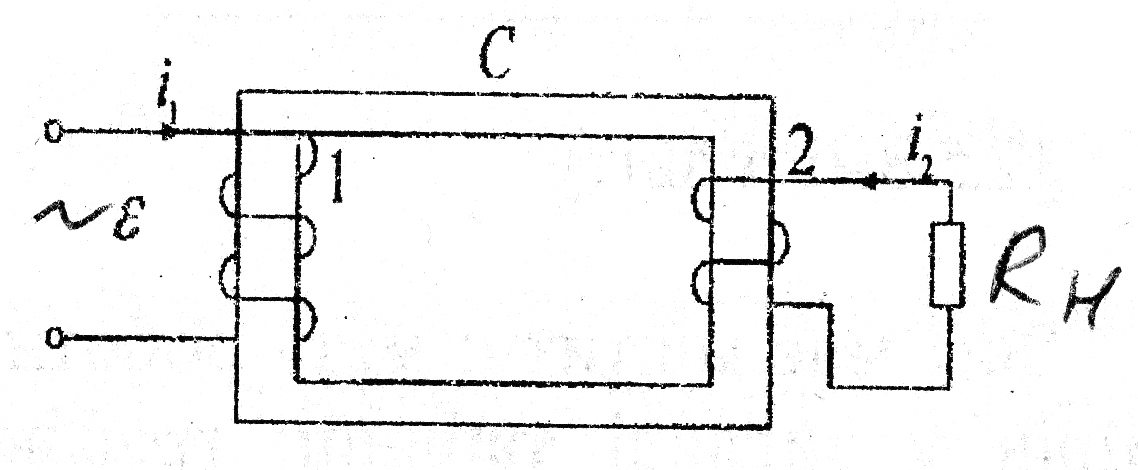
Рисунок 17.2 Трансформатор.

Якщо у котушці (1) протікає змінний струм i₁, то у феромагнітному осерді створюється змінний магнітний потік, частина якого ₂₁ проходить через котушку (2) та створює в ній ЕРС індукції:

(17.2)

де ₂₁ - потокозчеплення з контуром 2, яке створюється струмом i₁;

Ф₁ - магнітний потік котушки (1); N₂ - кількість витків другої котушки.

Розглянемо випадок, коли котушка (2) трансформатора розімкнена (навантаження R_н відсутнє). Цей випадок називається режимом холостого ходу трансформатора.

Запишемо співвідношення (17.21)у вигляді:

, (17.3)

де

(17.4)

називається динамічною взаємною індуктивністю або коефіцієнтом взаємоіндукції котушки (2) з котушкою (1).

Повний магнітний потік (потокозчеплення з котушкою 2):

₂₁₌ N₂Ф₁ =N₂B₁S (17.5)

створюється котушкою (1) (оскільки і₂ = 0) та залежить від індукції магнітного поля В₁ цієї котушки, кількості витків другої котушки N₂ та площі перерізу

осердя S.

Індукція магнітного поля, що створюється першою котушкою із числом витків N₁, довжиною l₁ і магнітною проникністю сердечника µ, визначається формулою:

(17.6)

Підставимо (17.6) у (17.5), а отримане співвідношення – у (17.4):

(17.7)

Дана формула дозволяє визначити коефіцієнт взаємоіндукції котушки (2) з котушкою (1) тільки для режиму холостого ходу. У цьому режимі в котушці (1) створюватиметься ЕРС , яка чисельно дорівнює ЕРС індукції.

Якщо вважати падіння напруги на опорі обмотки (1) малим через незначну величину опору цієї обмотки, то можна записати:

(17.8)

Поділивши (17.2) на (17.8), отримаємо можливість обчислення кількості витків однієї з обмоток, якщо відома кількість витків другої:

(17.9)

Перейдемо до розгляду режиму роботи, при якому в котушці (2) протікає струм і₂ - сумірний з величиною струму і₁, (0 < R_н <∞).

Струм і₂ (рис. 17.2) створює змінний магнітний потік у вторинній обмотці трансформатора. Цей повний потік поширюючись в осерді, прохо­дить крізь витки котушки (1) та створює в ній ЕРС взаємоіндукції:

(17.10)

де = N₁Ф₂ = N₁В₂S (B₂ - індукція магнітного поля котушки 2);

L₁₂ - коефіцієнт взаємоіндукції котушки (1) з котушкою (2):

. (17.11)

та є сумарними ЕРС взаємоіндукції, тому що в створенні змінного потоку осердя приймають участь струми і₁ та і₂. Враховуючи це, запишемо рівняння другого правила Кірхгофа для контуру (1):

.

Якщо падіння напруги на котушці (1) мале ( ≈ 0), то ≈ ≈U, де U -напруга джерела змінного струму, який змінюється за гармонічним законом:

(17.12)

де - амплітуда сили струму;

- циклічна частота.

Підставимо (17.12) до (17.3) та знайдемо ЕРС котушки (2):

(17.13)

Якщо знехтувати падінням напруги в котушці 2 через малий опір (R₂≈ 0.), можна вважати ≈U₂. Тоді:

(17.14)

Амплітудне значення напруги:

. (17.15)

Із співвідношення (17.15) знайдемо максимальне значення коефіцієнта взаємоіндукції другої котушки з першою:

(17.16)

Аналогічно можна визначити коефіцієнт взаємоіндукції першої котушки з

другою:

(17.17)

де U₀ - амплітуда напруги джерела струму;

і₀₂ - амплітуда сили струму в контурі (2);

= 2 , = 50 Гц.

Потужність Р₂, яка виділяється у зовнішньому колі цього контуру, завжди менша, ніж споживана з мережі потужність Р₁. Якщо навіть на опорі навантаження R_H вторинної обмотки трансформатора виділяється максимально допустима активна потужність, то і тоді вона буде менша за споживану. Це пов'язано з тим, що частина споживаної електричної енергії витрачається на перемагні­чування осердя (гістерезис) та його нагрівання (струми Фуко), а також на нагрі­вання обмоток трансформатора.

Відношення активної потужності Р₂, яка виділяється на опорі навантаження Р_н, до активної потужності Р₁, що споживається із мережі, називається ККД трансформатора:

(17.18)

де , - різниця фаз між i₀₁ та U₀₁; - різниця фаз між і₀₂ та U₀₂.

При опорах навантаження, близьких до оптимальних, та при невеликих коефіцієнтах трансформації різниці фаз в обмотках будуть малі і їх можна прирівняти ( ). Тому формула (17.18) для таких умов спрощується:

(17.19)

Порівнюючи (17.16) та (17.17), можна сказати, що відношення коефіцієн­тів взаємоіндукції обмоток чисельно дорівнює при зазначених вище умовах ККД трансформатора:

(17.20)

За законом збереження енергії потужності на первинній та вторинній обмотках трансформатора можна вважати однаковими Р₁=Р₂, якщо знехтувати тепловими втратами на їх активних опорах та в осерді, що обумовлені струмами Фуко. Тобто:

(17.21)

або через ефективні значення напруг та струмів:

(17.22)

Після підстановки виразів (17.2) і (17.78) та при ці рівняння можна переписати у вигляді такого співвідношення:

(17.23)

Величина k називається коефіцієнтом трансформації напруги. Вона визначає, у скільки разів ЕРС у вторинній обмотці трансформатора є більшою або меншою, ніж у первинної.