Информационное и программное обеспечение процесса вычисления интеграла ошибок Гаусса по заданным границам.

В практике судоремонта при обработке результатов измерений часто встречаются распределения, незначительно отличающиеся от нормального (распределения Гаусса). Признаками образования нормального распределения обычно принято считать совокупное влияние на технологический процесс материала изделий, метода контроля станочного оборудования и субъективных качеств человека-оператора.

На базе нормального распределения можно значительно сократить время обработки результатов измерений и принятия эффективных оперативных решений по управлению качеством продукции. Сокращение определяется использованием известных свойств нормального распределения.

Вершина кривой нормального распределения располагается над абсциссой, соответствующей математическому ожиданию m. Кривая имеет форму колокола и симметрична относительно перпендикуляра к оси абсцисс, проходящего через точку m и ординату её вершины (рис. выше) Ветви кривой нормального распределения асимптотически приближаются к оси абсцисс. Площадь под кривой нормального распределения для равна единице или 100 %.

Плотность нормального распределения выражается функцией

, (3.2)

где ; - среднее квадратическое отклонение нормального распределения.

При построении кривой, представленной на рис. 3.7., в уравнении (3.2) приняты следующие значения аргументов: математическое ожидание m = 0, среднее квадратическое отклонение , х = -3:0.01:3.

Вычисления выполнены с помощью оператора функции, помещённой в файле «sah133.m»:

% Файл "sah133.m"

% Функция для вычисления интеграла ошибок Гаусса.

function y=sah133(x);

sigma=1.0; m=0;

x=-3:0.01:3;

y=(1./(sigma*sqrt(2*pi)))*exp(-((x-m).^2)/(2*(sigma^2)));

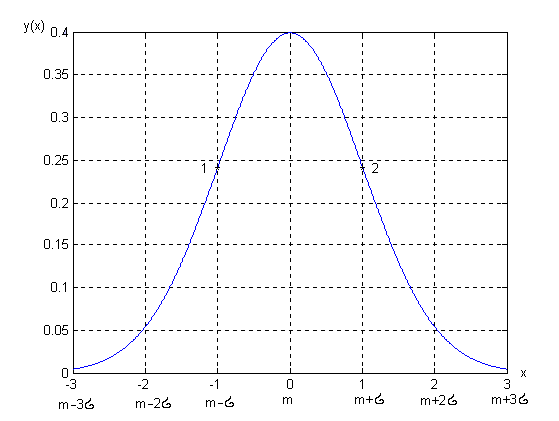
Рис. 3.7. Нормальное распределение.

Заметим, что колоколообразная кривая в точках 1 и 2 претерпевает перегиб. Расстояние по оси абсцисс между этими точками равно , что позволяет наглядно (по рисунку) оценить среднее квадратическое отклонение.

Обычно на практике кривую нормального распределения используют в интервале изменения , составляющем

.

В этом случае площадь под кривой равна 0.999, т.е. за пределами границ остаётся лишь 0.001 или 0.1 % площади. Если первое число характеризует статистическую надёжность, то второе – риск (ошибку первого рода).

Обычно статистическим допуском считают интервал , для которого рассчитана кривая, приведённая на рис. 3.7.

Для вычисления всей площади под кривой Гаусса необходимо воспользоваться уравнением:

, (3.3)

из которого следует, что эта площадь равна единице независимо от .

В процессе практического использования кривой нормального распределения для контроля качества продукции требуется рассчитывать (3.3) для различных значений верхней и нижней границ интегрирования, по модулю существенно меньших бесконечности. Поэтому значение интеграла

(3.4)

Функция , называемая интегралом ошибок Гаусса, представляет собой относительную частоту или вероятность того, что значение признака попадает в интервал от до . Если F – общее число наблюдений, образующих вариационный ряд, то частота вариационного ряда, которую следует ожидать в интервале , равна

.

Обычно для вычисления площадей по уравнению (3.4) используют специальные таблицы функции нормального распределения, которые в требуемый момент в распоряжении расчётчика могут отсутствовать. Вместе с тем можно предложить простую процедуру, позволяющую в среде MatLAB выполнять расчёты площадей для любых и в режиме прямых вычислений.

Процедура основана на использовании функции вида:

type sah133

% Файл "sah133.m"

% Функция для вычисления интеграла ошибок Гаусса.

function y=sah133(x);

sigma=1.0; m=0.000;

y=(1./(sigma*sqrt(2*pi)))*exp(-((x-m).^2)/(2*(sigma^2)));

В отличие от текста файла, приведённого выше, здесь отсутствует строка, в которой задаётся вариация аргумента .

Затем в режиме прямых вычислений необходимо произвести интегрирование функции. Для этого воспользуемся функцией quad:

. (3.5)

В результате получим значение интеграла, определённого границами , (См. уравнение (3.4)) с погрешностью .

Если требуется обеспечить иную величину погрешности, функцию следует записать в виде: и задать требуемое значение «tol».

Ниже приводятся результаты вычислений площадей s, ss, sss и ssss по уравнению (3.5):

>> s=quad('sah133',-3,3)

s = 0.9973

>> ss=quad('sah133',-3.29,3.29)

ss = 0.9990

>> sss=quad('sah133',-2.15,1.18)

sss = 0.8652

>> ssss=quad('sah133',-2.15,-1.18)

ssss = 0.1032

Рассмотрим примеры практического применения нормального распределения и изложенного способа нахождения площадей.

Пример 1.

Необходимо построить кривую нормального распределения, если математическое ожидание m = 8433 и среднеквадратическое отклонение . Определить площади между кривой и ординатами, проведёнными через точки:

х1	8263	8433	8473
х2	8490	8480	8533

Решение. Для построения войдём в редактор «edit» и вызовем файл «sah133.m». Внесём данные m и , определённые условием примера, а также зададим элементы вектора в виде последовательности . В результате будем иметь:

functiony=sah133(x);

sigma=56.5; m=8433;

x=8273:8593;

y=(1./(sigma*sqrt(2*pi)))*exp(-((x-m).^2)/(2*(sigma^2)));

Запишем файл с внесёнными изменениями в каталог MatLAB и войдём в эту среду. Инициируем работу файла. Получив вектор , в режиме прямых вычислений зададим

v = 8273:8593,

а затем построить график с помощью оператора

plot (v, y), grid

В результате получим кривую, представленную на рис. 3.8, в виде копии с экрана дисплея.

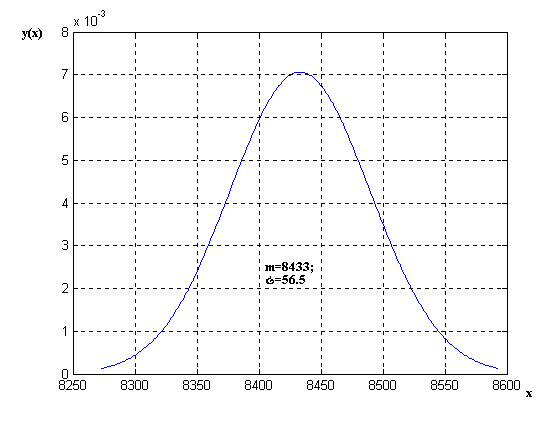
Рис. 3.8. Графические построения с помощью функции sah133.m.

Удалим из файла «sah133.m» строку

x=8273:8593.

Затем после коррекции в режиме прямых вычислений выполним расчёты:

% Файл "sah133.m"

function y=sah133(x);

sigma=56.5; m=8433;

y=(1./(sigma*sqrt(2*pi)))*exp(-((x-m).^2)/(2*(sigma^2)));

>> s1=quad('sah133',8263,8490)

s1 = 0.8422

>> s2=quad('sah133',8433,8480)

s2 = 0.2973

>> s3=quad('sah133',8473,8533)

s3 = 0.2011

Таким образом, между ординатами точек, согласно условию задачи, располагается