Заданные параметры движения

i	1	2	3
	1,0	1,2	2,0

Целью проектирования является определение параметров: .

Для решения задачи введем дополнительные переменные и . Для точки i = 1 запишем соотношения:

; (2.1)

. (2.2)

Из ∆ABCвыполняется равенство: . (2.3)

Подставив в выражение (2.3) значения и из (2.1) и (2.2), получим:

(2.4)

После преобразования (2.4) получим:

(2.5)

В окончательном виде запишем:

. (2.6)

Введем обозначения:

;

; (2.7)

.

Преобразуя (2.7) получим:

(2.8)

Для i-тых точек траектории составим систему уравнений:

, где i = 1, 2, 3. (2.9)

Систему уравнений (2.9) можно представить в матричном виде:

_{A*K = YV (2.10)}

где:

, , .

Решением системы уравнений (2.10) в среде MATLAB будет:

или (2.11)

Расчет траектории движения груза связан с выполнением программы

.

Из рис.2.1 видно, что при движении по заданной траектории при:

(2.12)

выполняется условие:

_, (2.13)

поэтому:

(2.14)

Поскольку: , то угол будет соответствовать:

(2.15)

Решение поставленной задачи в среде MATLAB в режиме прямых вычислений.

Пример 2.1

>>fi=[20 45 60];

>>si=[1.0 1.2 2.0];

>> fi1=fi*(pi/180); %Перевод угла " " в радианы.

>>yv=si.^2 %Вектор выхода.

yv = %Результат вычислений.

1.0000 1.4400 4.0000

>> A=[si'.*cos(fi1)' sin(fi1)' -ones(3,1)] %Определение матрицы А.

А= %Результат вычислений.

0.9397 0.3420 -1.0000

0.8485 0.7071 -1.0000

1.0000 0.8660 -1.0000

>> K=inv(A)*yv' %Расчет вектора К.

K =

12.3903

4.2991

12.1135

>> a1=K(1)/2

a1 =

6.1952

>> a3=K(2)/(2*a1)

a3 =

0.3470

>> a2=sqrt(a1^2+a3^2-K(3))

a2 =

5.1368

Для выполнения расчетов и построения траекторий движения элементов манипулятора, составим программу в режиме редактора.

Лабораторная работа № 1. "Расчет элементов манипулятора и построение траекторий движения при перемещении груза параллельно оси абсцисс"

Цель работы.

По программе файла pt1.m:

1.Определить размеры звеньев робота-манипулятора и высоту захвата груза.

2.Построить траектории движения элементов манипулятора в зависимости от плавного изменения угла поворота робота.

3.Построить положения звеньев манипулятора в зависимости от заданных углов поворота робота.

Вариант № 1.

% File pt1.m

fi=[20 45 60] %Исходные значения угла поворота.

%fi=[60 45 20] %Знак " % " в начале строки означает комментарий (не %исполняемый программой текст).

si=[1.0 1.2 2.0] %Исходные значения положения захвата груза.

%si=[2.0 1.2 1.0]

fi1=fi*(pi/180); %Перевод угла в радианы.

yv=si.^2

x2=fi;

A=[si'.*cos(fi1)' sin(fi1)' -ones(3,1)]

K=inv(A)*yv'

a1=K(1)/2 %Определение параметров манипулятора.

a3=K(2)/(2*a1)

a2=sqrt(a1^2+a3^2-K(3))

%Построение траекторий движения элементов %манипулятора.

fi=20:0.5:60; %Начальные и конечные значения угла с шагом 0,5.

fi1=fi*(pi/180);

fi2=pi/2-fi1+acos((a1*sin(fi1)-a3)/a2); %Расчетугла .

x1=a1*cos(fi1)-a2*cos(pi-fi1-fi2); %Расчеткоординат X и Y.

y1=a1*sin(fi1)-a2*sin(pi-fi1-fi2);

plot(fi,x1,'m-',fi,y1,fi,fi2,'k--',fi,fi1,'k'),grid %Графиктраекторийдвижения legend('si','a3','fi2','fi1',0) %элементовманипулятора.

hx=xlabel('fi,grad');

holdon; %Управление сохранением текущего

%графического окна (включение сохранения графика)

plot(x2,si,'ro') %Ввод в график красных кружков.

pause

holdoff; %Выключение сохранения графика.

%Построение координат положений звеньев манипулятора.

fi=[20 45 60];

%fi=[60 45 20];

fi1=(pi/180).*fi;

x=[0 a1*cos(fi1(1)) si(1)]; %Координаты

y=[0 a1*sin(fi1(1)) a3]; %положений

xa=[0 a1*cos(fi1(2)) si(2)]; %звеньев

ya=[0 a1*sin(fi1(2)) a3]; %манипулятора.

xb=[0 a1*cos(fi1(3)) si(3)];

yb=[0 a1*sin(fi1(3)) a3];

plot(x,y,x,y,'*',xa,ya,xa,ya,'*',xb,yb,xb,yb,'*'),axis([0 6 0 6]),grid

xlabel('X')

ylabel('Y')

Для решения предлагаются 15 вариантов задания исходных данных, приведенные в табл. 2.2.

Таблица 2.2

Варианты заданий для лаб. работы № 1

№ Варианта	fi	si	axis
1	[20 45 60]	[1.0 1.2 2.0]	[0 6 0 6]
2	[20 45 60]	[1.0 1.2 2.0]	[0 4 0 4]
3	[60 45 20]	[1.0 1.2 2.0]	[0 6 0 6]
4	[60 45 20]	[1.0 1.2 2.0]	[0 4 0 4]
5	[10 45 60]	[1.0 1.2 2.0]	[0 7 0 6]
6	[20 45 60]	[2.0 2.2 4.0]	[0 10 0 8]
7	[20 45 60]	[2.0 2.3 3.5]	[0 15 0 15]
8	[20 40 60]	[2.0 2.1 4.5]	[0 10 0 10]
9	[20 50 60]	[2.0 2.1 4.5]	[0 8 0 8]
10	[20 50 60]	[2.0 2.1 3.5]	[0 8 0 8]
11	[20 50 60]	[2.0 2.3 3.5]	[0 9 0 9]
12	[20 50 60]	[4.5 2.3 2.0]	[0 7 0 7]
13	[20 40 60]	[4.5 2.3 2.0]	[0 5 0 5]
14	[20 50 60]	[4.5 2.5 2.0]	[0 5 0 5]
15	[20 45 60]	[4.5 2.5 2.0]	[0 7 0 7]

Выполнение программы возможно в режиме Редактора: пункт меню Отладка (Debug)  Запуск (Run), либо в Командном Окне (CommandWindow): набрать: >> pt1, затем нажать Enter.

Результаты решения задачи для первого варианта.

fi =

20 45 60

si =

1.0000 1.2000 2.0000

yv =

1.0000 1.4400 4.0000

A =

0.9397 0.3420 -1.0000

0.8485 0.7071 -1.0000

1.0000 0.8660 -1.0000

K =

12.3903

4.2991

12.1135

a1 =6.1952; a3 =0.3470; a2 = 5.1368;

Нажимаем любую клавишу на клавиатуре и получаем рис.2.3.

Рис.2.3 График положений звеньев манипулятора

В окне Редактора в файле pt1.m вводим значения для второго варианта, сохраним файл pt1.m со значениями второго варианта. Затем в пункте меню "Отладка" выполним команду "Запуск". Либо в Командном Окне выполняем программу с новыми значениями, предварительно в Командном Окне выполняем команду: "CLC" (очистка экрана).

Лабораторная работа № 2. "Компьютерное моделирование положений двухзвенного робота - манипулятора по любой заданной траектории движения выходных координат"

Рассмотрим кинематическую схему манипулятора, приведенную на рис.2.4.

Пусть заданны:

- длины плеч звеньев манипулятора;

(x,y)-координаты захвата манипулятора при движении груза.

Необходимо определить углы: .

Из ∆ОВC по теореме Пифагора длина стороны ОВ имеет значение .

Для решения поставленной задачи, используя теорему косинусов, из выражений (2.16) и (2.20) определяем углы . Углы находим по выражениям (2.18), (2.19).

; (2.16)

; (2.17)

; (2.18)

; (2.19)

; (2.20)

. (2.21)

Из рис.2.4 определяем значения текущих координат траектории движения груза:

; (2.22)

. (2.23)

Расчет положений двухзвенного робота – манипулятора по заданной траектории движения выходных координат в среде MATLAB выполним в лабораторной работе № 2.

Лабораторная работа №2

Цель работы.

По программе файла pt2.m:

1.Произвести расчеты значений углов α и β расположения звеньев робота-манипулятора, используя заданные координаты захвата груза x и y.

2.Рассчитать координаты пяти положений звеньев манипулятора.

3.Построить график пяти положений звеньев двухзвенного манипулятора.

%File pt2.m

ZA=[9 7 5 3 1;1 3 5 7 9] %Вариант 1. Матрица .

%Заданная траектория движения груза в %координатах (x,y).

a1=6.1952;a2=5.1368; %Заданная длина плеч звеньев %манипулятора.

ZB=ZA.^2; %Поэлементное возведение в квадрат

%матрицы ZA ( ).

ZC=sum(ZB); %Вектор суммы квадратов элементов матрицы ZB.

S=ZC.^0.5; %Поэлементное возведение вектора ZC в степень 0,5.

SK=S.^2; %Поэлементное возведение вектора S в квадрат.

V=ZA(2,:)./ZA(1,:); %Вектор поэлементного деления значений %координат у на х матрицы ZA.

alf2=atan(V); %Расчет значений угла α₂.

ch=a1^2-a2^2+SK; %Расчет значений вектора ch.

zn=2*a1.*S; %Расчет значений вектора zn.

alf1=acos(ch./zn); %Расчет по теореме косинусов значений угла α₁.

alf=alf1+alf2; %Расчет значений угла α.

ch1=a1^2+a2^2-SK; %Расчет значений вектора ch1.

zn1=2*a1*a2; %Расчет числа zn1.

bet=acos(ch1./zn1); %Расчет по теореме косинусов значений угла β.

alfg=(180/pi)*alf; %Значения угла α в радианах.

betg=(180/pi)*bet; %Значения угла β в радианах.

[alfg;betg] %Матрица значений углов α и β.

x=a1*cos(alf)+a2*cos(pi-alf-bet); %Расчет выходных координат х и у

y=a1*sin(alf)-a2*sin(pi-alf-bet); %траекторийдвижениягруза.

[x;y] %Матрица значений координат х и у.

X=[zeros(1,5) a1*cos(alf) x]; %Расчет координат X,Y звеньев траекторий

Y=[zeros(1,5) a1*sin(alf) y]; %движения манипулятора.

W=[X;Y] %Матрица элементов манипулятора в координатах х и у.

R1=[W(:,1) W(:,6) W(:,11)] %Матрицы [2*3] координат х и у, для трех

R2=[W(:,2) W(:,7) W(:,12)] %точек звеньев манипулятора

R3=[W(:,3) W(:,8) W(:,13)] %(начало 1-го звена, конец 1-го начало

R4=[W(:,4) W(:,9) W(:,14)] %2-го звеньев, конец 2-го звена) и для

R5=[W(:,5) W(:,10) W(:,15)] %5-ти положений звеньев манипулятора.

plot(R1(1,:),R1(2,:),R1(1,:),R1(2,:),'*',R2(1,:),R2(2,:),...

R2(1,:),R2(2,:),'*',R3(1,:),R3(2,:),R3(1,:),R3(2,:),'*',...

R4(1,:),R4(2,:),R4(1,:),R4(2,:),'*',R5(1,:),R5(2,:),...

R5(1,:),R5(2,:),'*'),grid %Построение графика.

Результаты решения в среде MATLAB.

Вариант 1.

ZA =

9 7 5 3 1 %Значения заданной траектории движения

1 3 5 7 9 %груза в координатах х,y.

ans =

39.4384 65.3175 89.9613 108.9203 116.7581 %Матрица углов α

105.7092 83.8965 76.5841 83.8965 105.7092 %и β в радианах.

ans =

9.0000 7.0000 5.0000 3.0000 1.0000 %Матрица координат х,у.

1.0000 3.0000 5.0000 7.0000 9.0000

W =

Columns 1 through 7

0 0 0 0 0 4.7846 2.5871

0 0 0 0 0 3.9355 5.6292

Columns 8 through 14

0.0042 -2.0088 -2.7892 9.0000 7.0000 5.0000 3.0000

6.1952 5.8605 5.5318 1.0000 3.0000 5.0000 7.0000

Column 15

1.0000 %Матрица 5-ти положений звеньев манипулятора

9.0000 %в координатах X и Y.

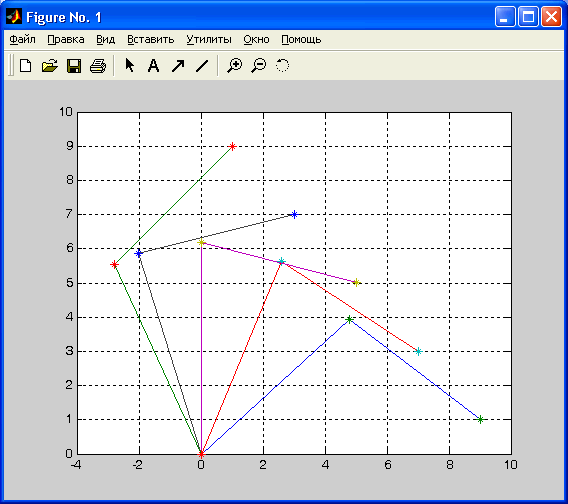
Рис. 2.5 График положений двухзвенного манипулятора

Таблица 2.3

Варианты заданий для лаб. работы № 2

№ Варианта задания	ZA
1	[4.8 6.4 7 6.4 4.8; -4.2 -2.4 0 2.4 4.2]
2	[4.8 6.4 7 6.4 4.8; -4.2 -2.4 0 2.4 4.2]
3	[3.2 6.4 7 6.4 3.2; -4.3 -2.0 0 2.0 4.3]
4	[2.4 5 6 5 3.6; -9.1 -4 0 4 7]
5	[1.3 1.6 3.2 4.8 6.4; 8.9 8.8 8.4 7.4 5.5]
6	[0.5 2.6 3.2 4.8 5.4; -7.9 -6.8 0.4 3.4 1.5]
7	[1.5 1.6 2.2 3.8 4.4; 0.9 1.8 2.4 3.4 5.5]
8	[2.3 3.6 4.2 6.8 8.4; 7.9 6.8 5.4 3.4 1.5]
9	[1 2 3 6 7; 8 6 4 2 0.5]
10	[8.5 6.6 2.2 1.8 0.4; 8.9 5.8 0.4 -3.4 -1.5]
11	[5.8 6.4 7.5 6.4 4.8; -4.2 -2.4 0 2.4 4.2]
12	[-3.2 -6.4 -7 -6.4 -3.2; 7.3 4.0 0 -2.0 -4.3]
13	[-1.4 -5.7 -6.4 -5 -2.6; -9.1 -4 0 4 7]
14	[-1.5 -1.6 -2.2 -3.8 -4.4; -0.9 -1.8 -2.4 -3.4 -5.5]
15	[5.8 6.4 7.5 6.4 4.8; -0.9 -1.8 -2.4 -3.4 -5.5]

%Матрицы координат X,Y:

R1 =

0 4.7846 9.0000 %для 1-го положения звеньев а₁, а₂.

0 3.9355 1.0000

R2 =

0 2.5871 7.0000 %для 2-го положения звеньев а₁, а₂.

0 5.6292 3.0000

R3 =

0 0.0042 5.0000 %для 3-го положения звеньев а₁, а₂.

0 6.1952 5.0000

R4 =

0 -2.0088 3.0000 %для 4-го положения звеньев а₁, а₂.

0 5.8605 7.0000

R5 =

0 -2.7892 1.0000 %для 5-го положения звеньев а₁, а₂.

0 5.5318 9.0000