Оптическое преобразование Фурье
Анализатор частот у функции, Анализатор волновых чисел у
зависящей от времени – функции, зависящей от координаты
спектрометр
На призму с дисперсией падает Плоская волна падает
волна с зависимостью на транспарант с
от
времени
.
коэффициентом пропускания
.
Призма осуществляет Линза осуществляет
преобразование преобразование
время → частота, координата → волновое число,
,
,
– распределение амплитуд
– распределение амплитуд
по углам и частотам. в фокальной плоскости
,
,
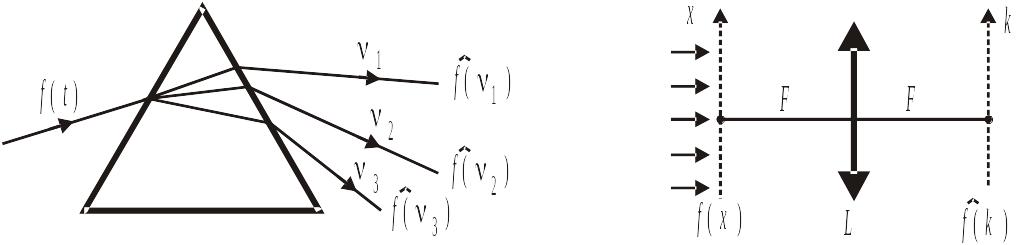
Теоремы Фурье
Линейность преобразования
.
(1.5)
Следует из линейности операции интегрирования в (1.1).
Масштабное преобразование аргумента функции
.
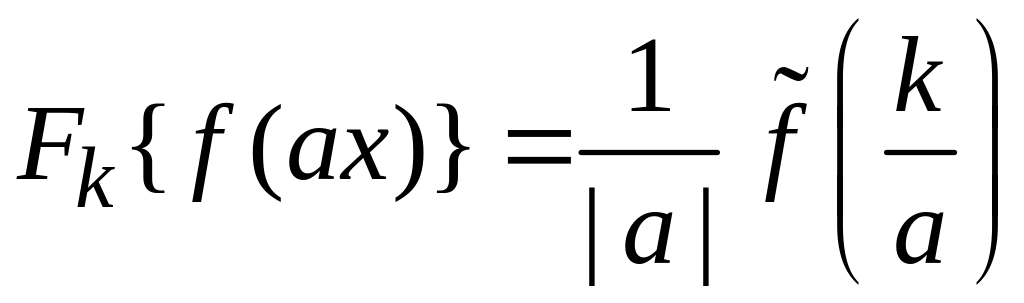(1.6)
Доказательство:
Из (1.1)
.
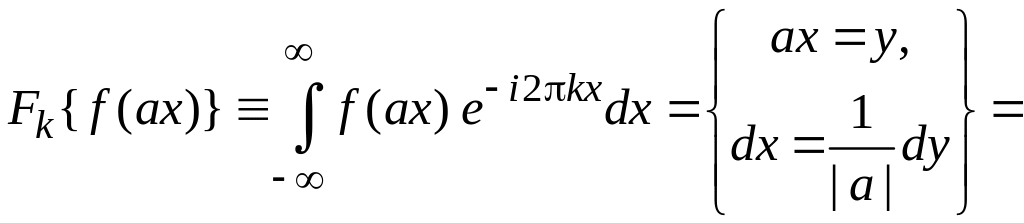
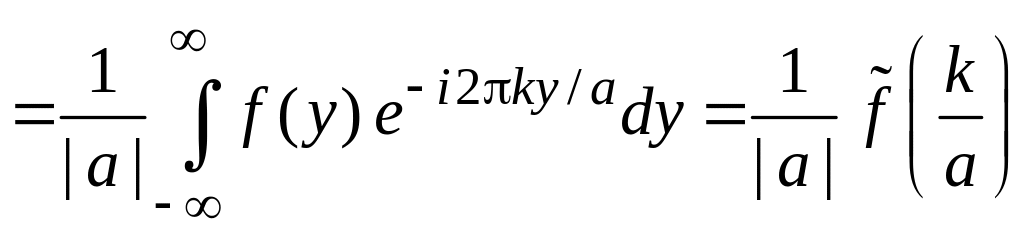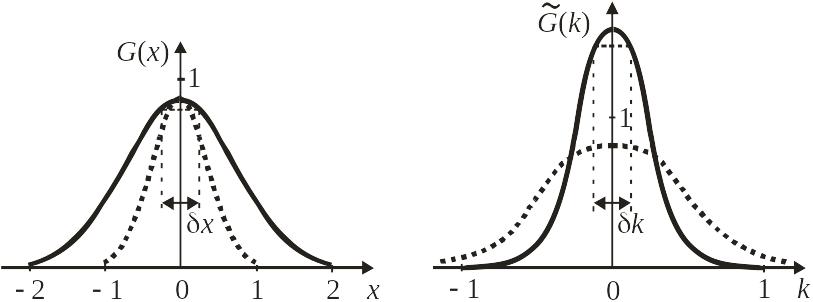
Пример: Функция Гаусса
,
.
При
масштабном преобразовании
с
– сжатие по x
в 2 раза (переход от сплошной линии к
пунктирной), растяжение по k
и уменьшение амплитуды в 2 раза.
Инверсия аргумента
Из
(1.6) при
.
(1.7)
Следовательно, четности функции и образа совпадают.
Теорема о частотной полосе
,
(1.8)
где дисперсии
;
.
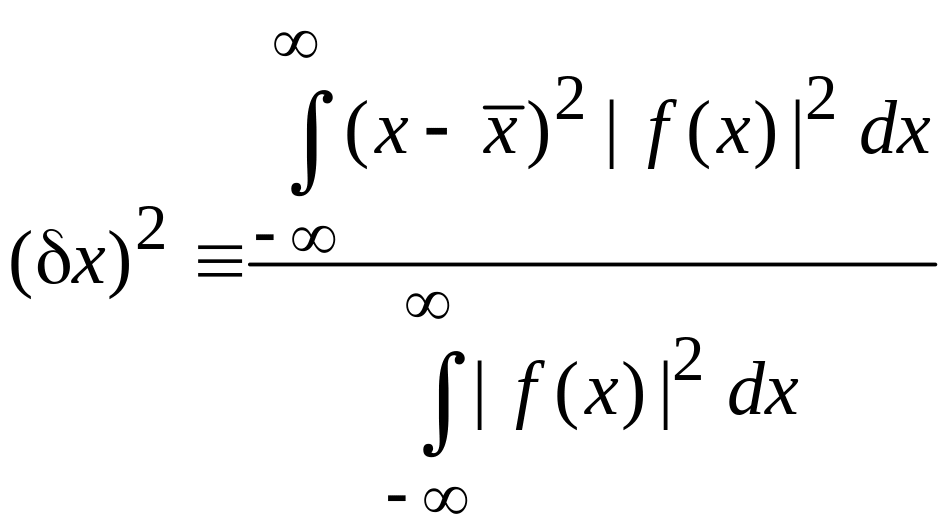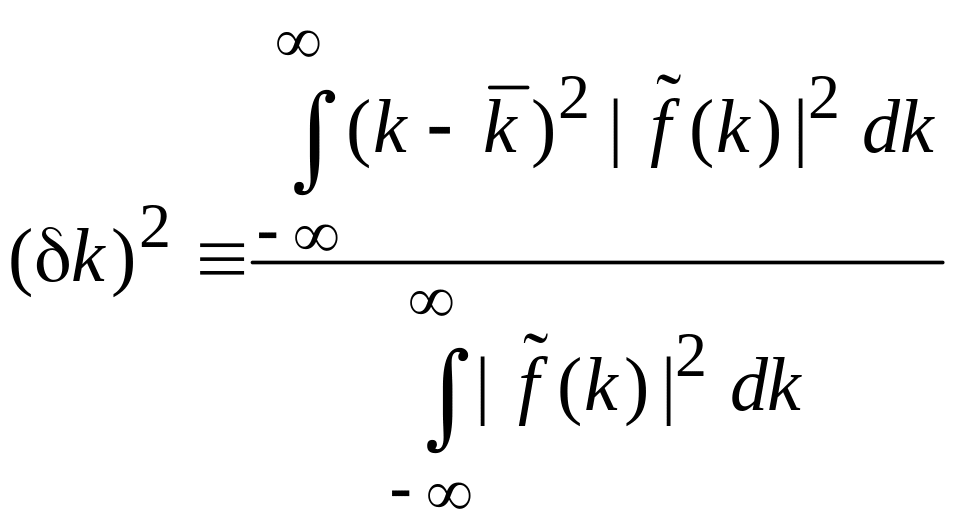Уменьшение
пространственной протяженности функции
приводит к увеличению ее частотной
протяженности
,
и наоборот.
Равенство в (1.8) выполняется для функции Гаусса
,
,
,
,
.
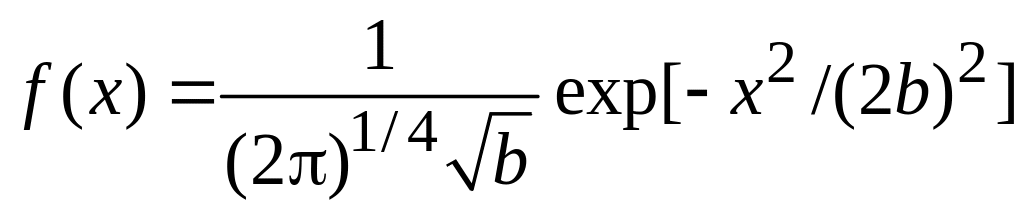Смещение аргумента
.
(1.9)
Доказательство:
Используем (1.1)
,
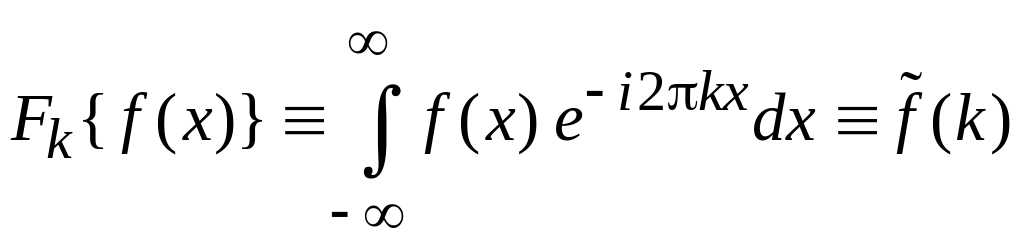получаем
.
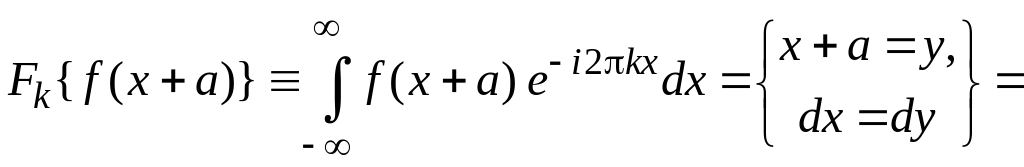
Фазовый сдвиг
.
(1.10)
Доказательство:
Из (1.1)
.
Комплексное сопряжение
,
(1.11)
Доказательство:
Из (1.1)
,
.
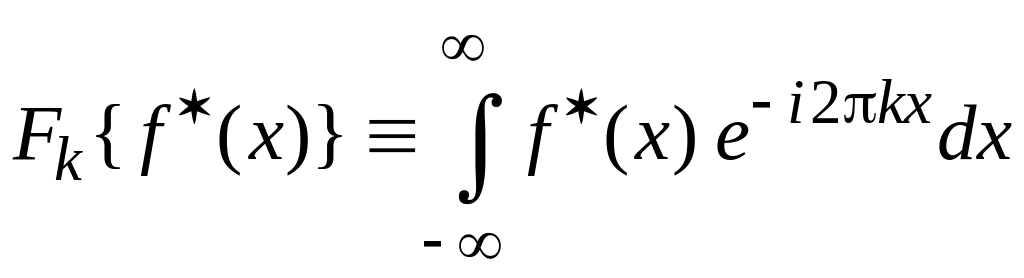Следствия (1.7) и (1.11)
,
:
1) если – четная и вещественная, то вещественная.
Доказательство:
Используем
,
,
тогда
;
2) если – вещественная и нечетная, то мнимая;
3) если – мнимая и четная, то мнимая;
4) если – мнимая и нечетная, то вещественная.
Теорема Парсеваля
.
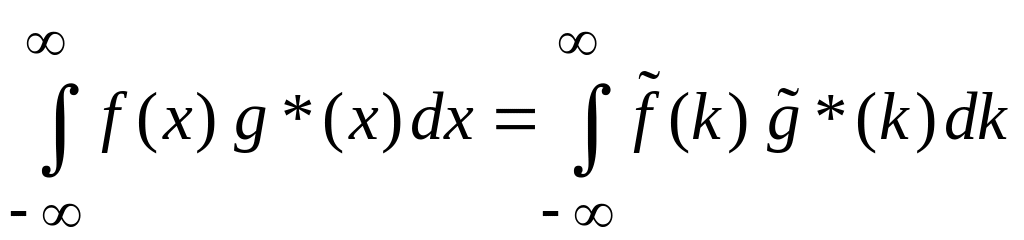(1.14)
В физике выражает закон сохранения энергии и вероятности при преобразовании Фурье.
Марк-Антуан Парсеваль (1755–1836) – французский математик. Исследовал дифференциальные уравнения и функции комплексного переменного. Доказал «теорему Парсеваля» в 1799 г.
Доказательство:
Используем (1.1) и (1.2)
,
.
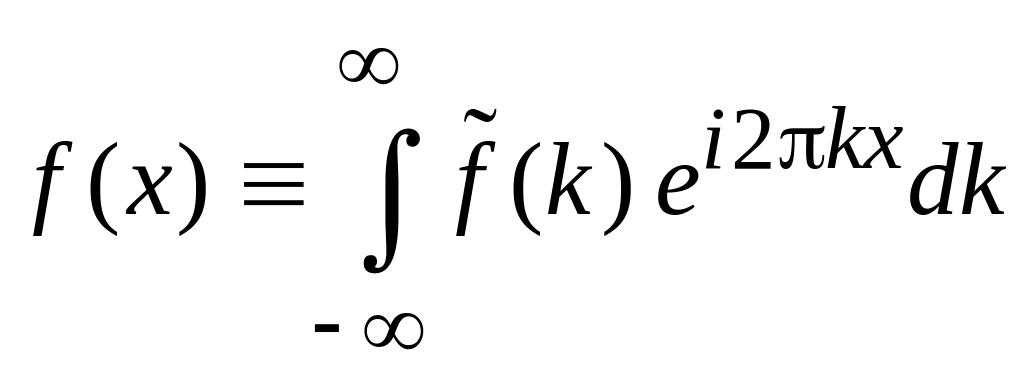Получаем
,
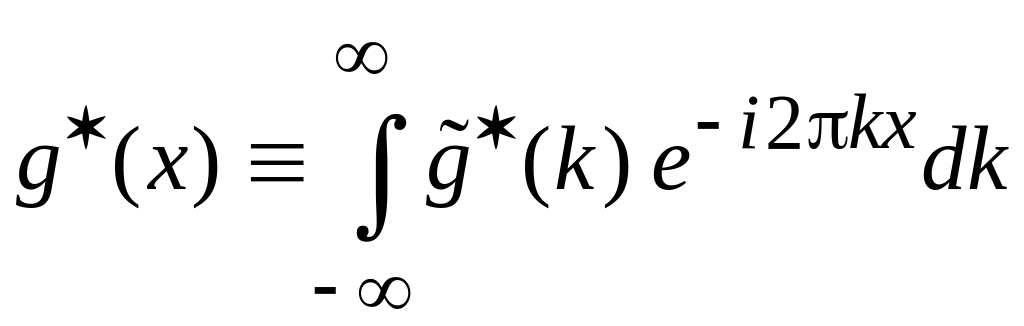тогда
=
,
где изменен порядок интегрирований.