Гильбертово пространство с дискретным базисом

Гильбертово пространство – множество комплексных, квадратично интегрируемых функций, для которых определено скалярное произведение. Ввел Гильберт в 1910 г.

Давид Гильберт (1862–1943)

Базис ортов

, ,

N – размерность пространства – конечное или бесконечное число;

–комплексная, квадратично интегрируемая функция, определенная на интервале аргумента .

Скалярное произведение определяется в виде

, (0.5)

где – вещественная весовая функция; – комплексно сопряженная функция.

Комплексное сопряжение

вещественное число ;

мнимая единица , ;

формула Эйлера ,

, ,

,

.

Формулу получил Эйлер в 1740 г.

Леонард Эйлер (1707–1783)

Комплексное число

,

;

квадрат модуля числа

;

.

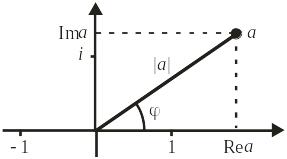
Представление комплексного числа

точкой на плоскости

Условие ортонормированности базиса

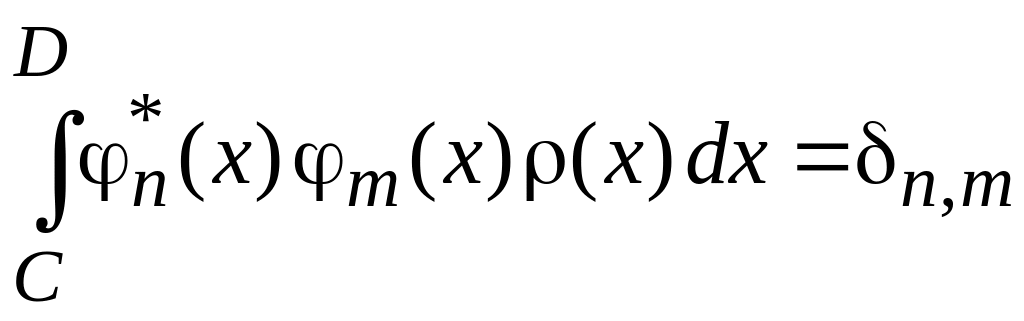. (0.6)

Разложение функции по базису

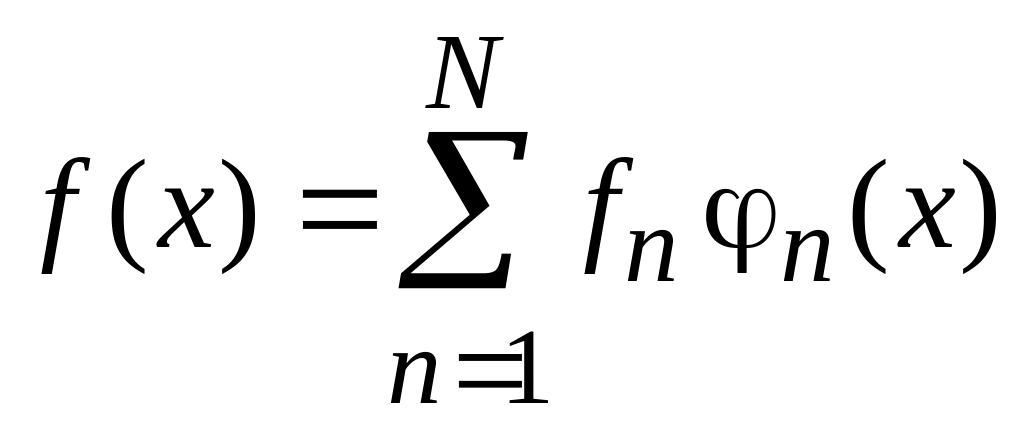, (0.7)

где – множество проекций, или спектр функции f(x).

Проекция функции на орт

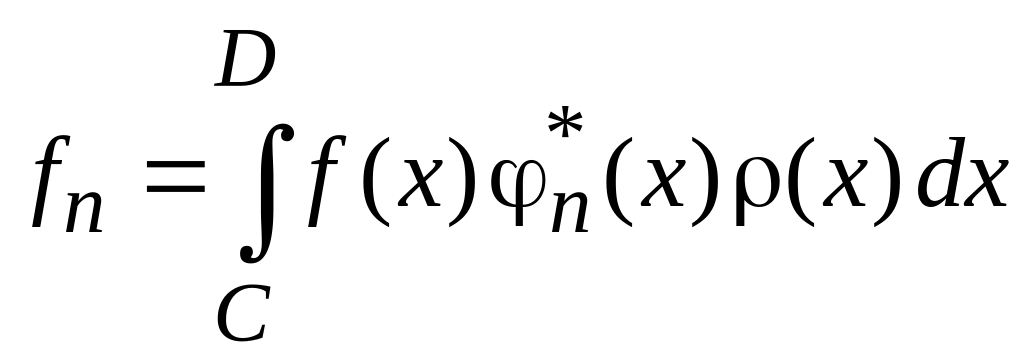. (0.8)

Подстановка (0.8)→(0.7) дает тождество

,

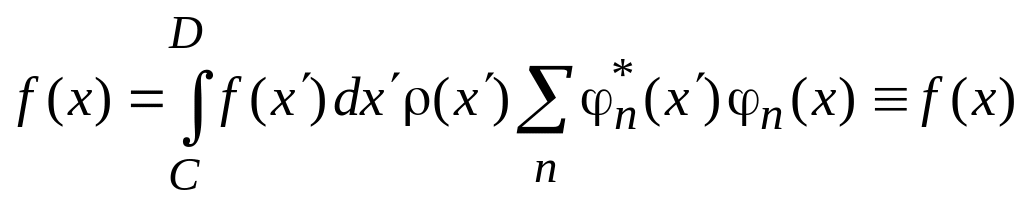если базис полон.

Условие полноты базиса

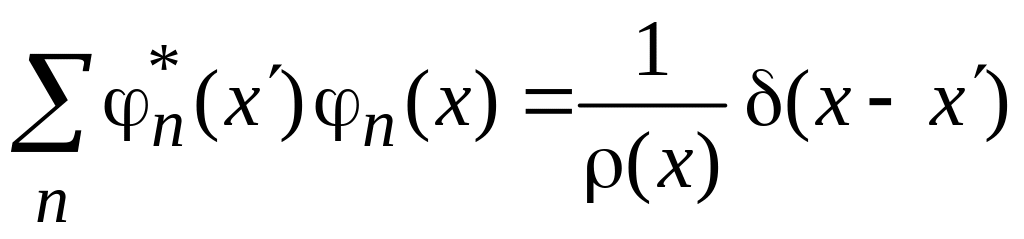, (0.9)

где – дельта-функция,

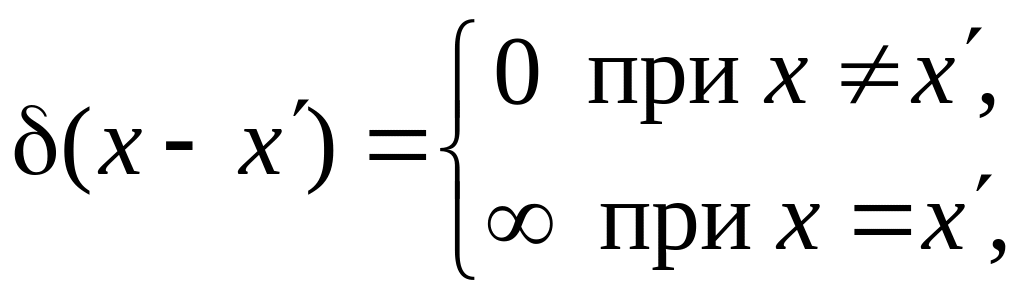
– фильтрующее свойство.

Теорема Парсеваля – является теоремой Пифагора в пространстве функций

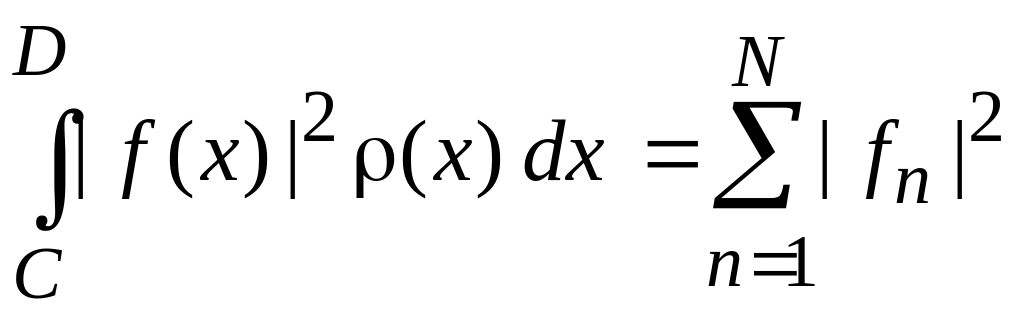, (0.10)

где

, .

Теорема доказывается подстановкой (0.7) и использованием (0.9). Теорему получил Мари-Антуан Парсеваль (1755–1836) в 1799 г.

Гильбертово пространство с непрерывным базисом

Базис ортов , где ; k – непрерывное, . Размерность пространства бесконечная.

Условие ортонормированности базиса

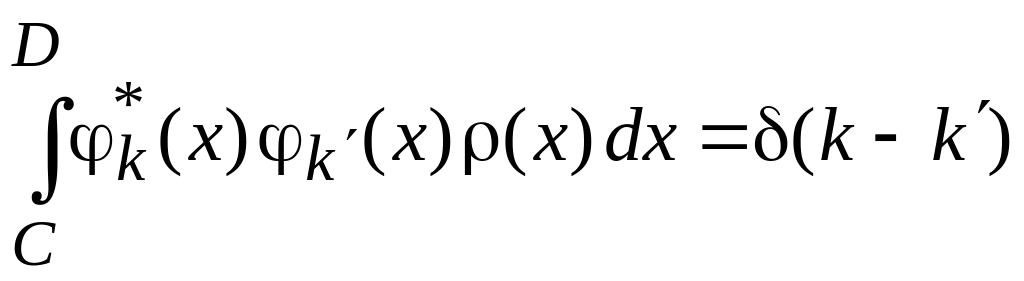, (0.11)

где – дельта-функция.

Разложение функции по базису

. (0.12)

Спектр непрерывный

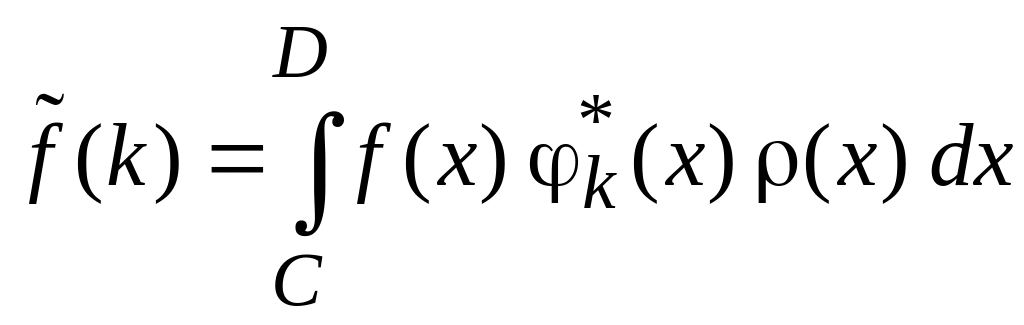. (0.13)

Совпадение спектров функций означает равенство функций.

Подстановка (0.12) в (0.13) дает тождество с учетом (0.11) и фильтрующего свойства дельта-функции.

Условие полноты базиса

. (0.14)

Подстановка (0.13) → (0.12) с учетом (0.14) дает тождество.

Теорема Парсеваля

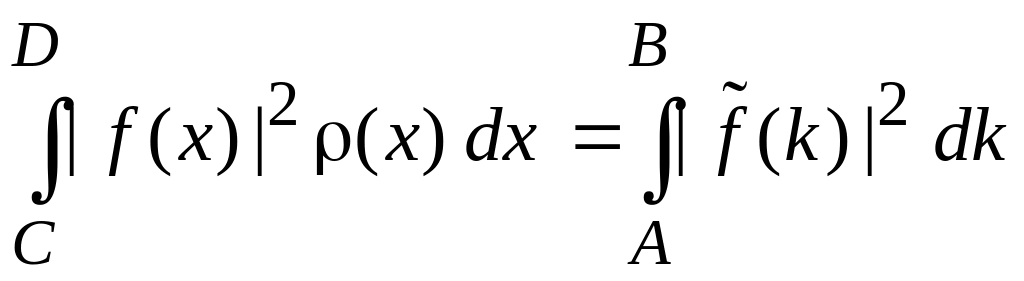(0.15)

доказывается с помощью (0.11) и (0.12), или с помощью (0.13) и (0.14).

Преобразование фурье

Древнегреческий математик Аполлоний представил сложное движение планеты в виде суммы равномерных вращений по окружностям – эпициклам в III в до н.э.

Французский математик Фурье разложил функцию по гармоническим составляющим в 1807 г.

Аполлоний Пергский – (ок. 262 – ок. 190 до н.э.)

Жан Батист Жозеф Фурье (1768–1830)

Бесконечномерный базис гармонических функций

, ; .

Орт является решением волнового уравнения Гельмгольца

,

и является плоской волной, распространяющейся вдоль оси x:

.

Герман Гельмгольц (1821–1894)

Базис с непрерывным спектром удовлетворяет:

условию ортонормированности

,

условию полноты

.

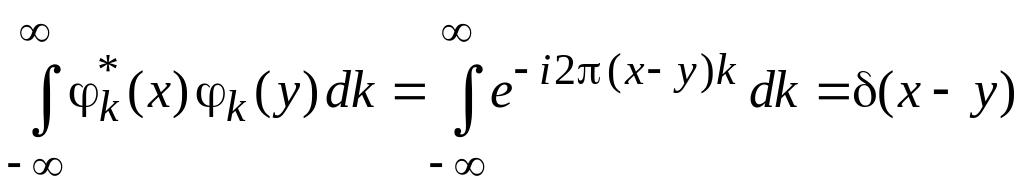Преобразование Фурье – разложение функции по базису

, (1.1)

, (1.2)

– оператор Фурье, действующий на функцию с аргументом x, находящуюся в скобках , и дающий функцию, зависящую от k;

– оператор обратного преобразования Фурье, действующий на функцию с аргументом k, и дающий функцию, зависящую от x;

– Фурье-образ или спектр функции ;

k и x – Фурье-сопряженные переменные, – безразмерная;

– ядро преобразования, не зависящее от преобразуемой функции.

Преобразование Фурье выполняет, например, входной контур радиоприемника, или телевизора при помощи колебательного контура.