Гиперболический тренд

Одна из простых форм гиперболы – уравнение, имеющие следующий вид:

При расчете гиперболического тренда нельзя нумеровать периоды времени от середины ряда, так как значения 1/ должны быть всегда положительными.

Основные свойства гиперболического тренда:

• При > 0 – уровни медленно снижаются и y 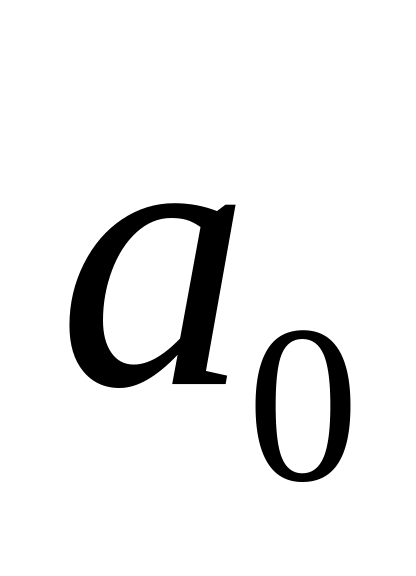; также уменьшаются отрицательные абсолютные изменения и величины положительного ускорения; цепные темпы изменения растут и стремятся к 100%.

• При < 0 – уровни замедлено возрастают и 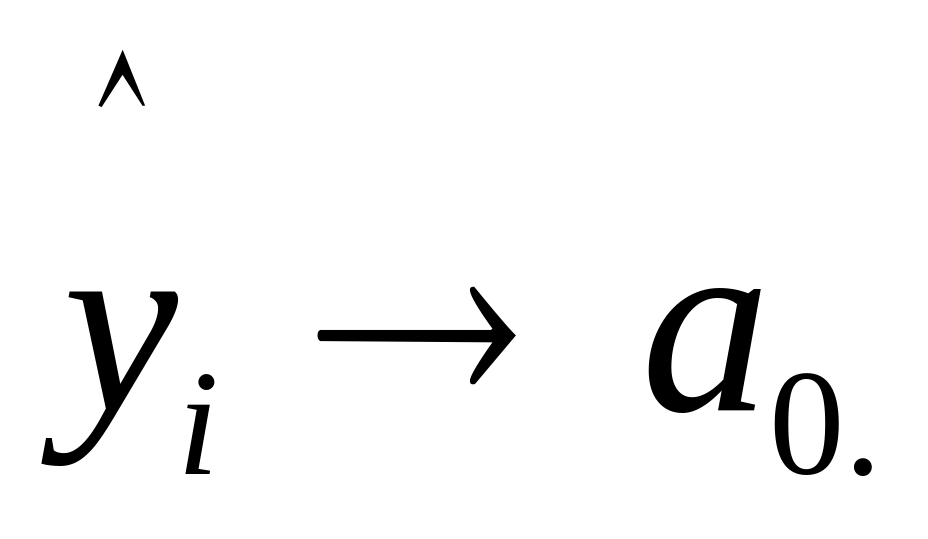;также уменьшаются положительные абсолютные изменения и величины отрицательного ускорения; цепные темпы роста замедленно уменьшаются, стремясь к 100%.

Значение параметров гиперболы

Параметр	Содержание параметра
	Свободный член гиперболы, предел, к которому стремится уровень ряда
	Основной параметр гиперболы: Если > 0, то этот тренд выражает тенденцию замедляющегося снижения уровней и при t , Если параметр < 0, то с возрастанием t, т.е. с течением Времени, уровни тренда возрастают и стремятся к величине при t .

Экспоненциальный тренд

Экспоненциальным трендом называют тренд, который выражается следующим уравнением.

Уравнение экспоненты (экспоненциальный тренд):

или .

Экспоненциальный тренд характерен процессом, развивающимся в среде, не создающим никаких ограничений для роста уровней. Следовательно, на практике такие явления встречаются только в ограниченном промежутке времени, поскольку любая среда рано или поздно создаёт ограничения.

Значения параметров уравнения экспоненты

Параметр	Содержание параметра
k	Постоянный темп изменения уровней (цепной). Если k > 1, то имеется тренд с возрастающими уровнями, причем это возрастание не просто ускоренное, а с возрастающим ускорением и возрастающими производными более высоких порядков. Если k < 1, то имеется тренд, выражающий тенденцию постоянного, но замедляющегося сокращения уровней, причём замедление непрерывно усиливается. Экстремума экспоненты не имеет и при t стремится либо к при k > 1, либо к 0 при k < 1.
a	Свободный член экспоненты равен выровненному уровню, т.е. уровню тренда в момент или период, принятый за начало отсчета времени ( при t = 0 ).

Основные свойства экспоненциального тренда:

• Абсолютные изменения уровней тренда пропорциональны самим уровням;

• Экспонента экстремумов не имеет: при k > 1 тренд стремится к + , k < 1 тренд стремится к 0;

• Уровни тренда представляют собой геометрическую прогрессию: уровень периода с номером t > m есть ;

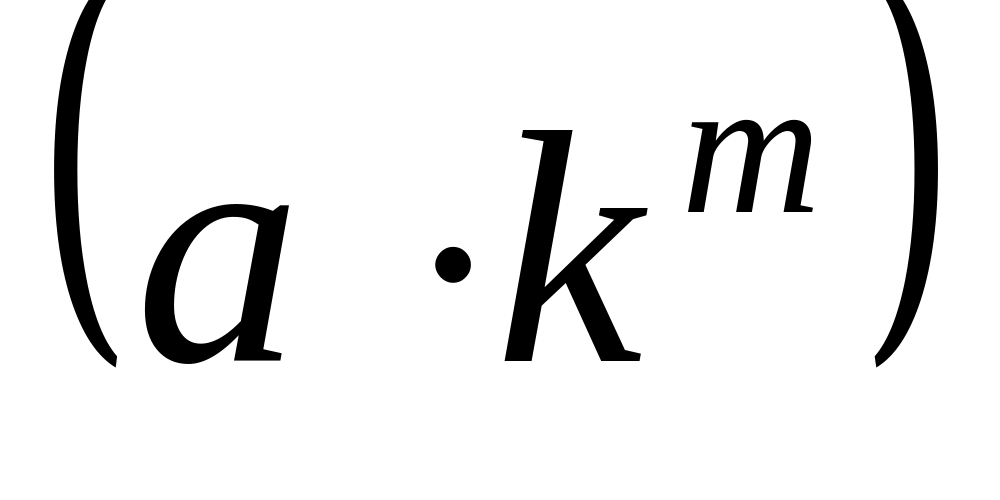• При k > 1 тренд отражает неравномерно ускоряющийся рост уровней, при k < 1 тренд отражает неравномерно замедляющееся уменьшение уровней;

• Экспонента не имеет постоянных производных любого порядка по времени (постоянен только цепной темп изменения).