- •Министерство сельского хозяйства рф
- •080200 "Менеджмент"
- •Содержание
- •Предисловие
- •Тема 1. Введение в эконометрику
- •Предмет эконометрики
- •Основные задачи эконометрики
- •3. Особенности эконометрического метода
- •4. Типы данных и моделей
- •Вопросы для самоконтроля:
- •Тема 2. Основы эконометрического анализа
- •Понятие о корреляции и регрессии
- •2. Сущность корреляционно-регрессионного анализа и моделирования
- •3. Общие принципы проверки статистических гипотез
- •Понятие о корреляции и регрессии
- •2. Сущность корреляционно-регрессионного анализа и моделирования
- •3. Общие принципы проверки статистических гипотез
- •Вопросы для самоконтроля:
- •Тема 3. Однофакторные корреляционно - регрессионные модели и возможности их применения для анализа и прогноза
- •1. Парная регрессия и корреляция в эконометрических исследованиях
- •2. Особенности оценки параметров нелинейных моделей
- •3. Методика построения модели парной регрессии
- •1. Парная регрессия и корреляция в эконометрических исследованиях
- •2. Особенности оценки параметров нелинейных моделей
- •3. Методика построения модели парной регрессии
- •Линейная модель.
- •Равносторонняя гипербола.
- •Степенная модель.
- •Вопросы для самоконтроля:
- •Тема 4: многофакторная корреляция и регрессия
- •Решение вопроса о спецификации модели
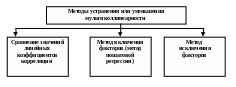
- •Описание методов устранения или уменьшения мультиколлинеарности:
- •2. Уравнение многофакторной регрессии, его построение и интерпретация
- •3. Система показателей тесноты многофакторной связи
- •4. Методика проведения анализа на основе построения уравнения многофакторной линейной регрессии
- •5. Предпосылки метода наименьших квадратов
- •Соблюдение требований, которым должен удовлетворять ряд остатков.
- •Вопросы для самоконтроля:
- •Тема 5. Системы эконометрических уравнений
- •1.Системы уравнений в эконометрике
- •2. Модели системы одновременных уравнений и их составляющие
- •3. Решение проблем идентификации
- •4. Методы решения систем одновременных уравнений
- •Косвенный метод наименьших квадратов
- •Вопросы для самоконтроля:
- •Тема 6. Временные ряды. Основные типы трендов
- •Виды и построение временных рядов
- •Основные этапы изучения, моделирования и прогнозирования временных рядов
- •2. Основные типы трендов
- •1. Метод разности средних двух частей одного и того же ряда.
- •Определение критерия Стьюдента и его сравнение с табличным значением.
- •Линейный тренд
- •Характеристика параметров линейного тренда.
- •Параболический тренд
- •Гиперболический тренд
- •Экспоненциальный тренд
- •Логарифмический тренд
- •Логарифмический тренд обладает следующими свойствами:
- •3. Методы распознавания типа тренда и оценки его параметров
- •4. Понятие сезонных колебаний и сезонной составляющей
- •Вопросы для самоконтроля:
- •Тема 7. Автокорреляция временных рядов
- •1. Автокорреляция и авторегрессия
- •Виды автокорреляции:
- •Свойства коэффициента автокорреляции:
- •2. Методы изучения автокорреляции
- •3. Принимают или отклоняют каждую гипотезу с вероятностью (1-α) на основе следующего рисунка:
- •Взаимосвязь временных рядов
- •Методы коррелирования:
- •4 Коинтеграция: понятие, методы проверки гипотезы о ее наличии
- •Методы проверки гипотезы о коинтеграции:
- •Вопросы для самоконтроля:
- •Глоссарий
- •Литература
- •Приложение 1.
- •Приложение 2. Функция стандартного нормального распределения
- •Приложение 5.
- •Вопросы для зачета
Вопросы для самоконтроля:
Раскройте методику вычисления параметров парного линейного уравнения регрессии.
Поясните смысл коэффициента регрессии, назовите способы его оценивания, покажите, как он используется для расчета мультипликатора в функции потребления.
Что такое число степеней свободы и как оно определяется для факторной и остаточной сумм квадратов?
Какова концепция F-критерия Фишера?
Как оценивается значимость параметров уравнения регрессии?
В чем отличие стандартной ошибки положения линии регрессии от средней ошибки прогнозируемого индивидуального значения результативного признака при заданном значении фактора?
Какой нелинейной функцией может быть заменена парабола второй степени, если не наблюдается смена направленности связи признаков?
Запишите все виды моделей, нелинейных относительно: включаемых переменных; оцениваемых параметров.
В чем отличие применения МНК к моделям, нелинейным относительно включаемых переменных и оцениваемых параметров?
Как определяются коэффициенты эластичности по разным видам регрессионных моделей?
Назовите показатели корреляции, используемые при нелинейных соотношениях рассматриваемых признаков.
Перечислите особенности сельскохозяйственного производства, его анализа и моделирования.
Назовите основные типы нелинейных регрессионных моделей, применяемые в сельскохозяйственном производстве.
Возможность применение регрессионных моделей в прогнозировании и в анализе хозяйственной деятельности
Тема 4: многофакторная корреляция и регрессия
План лекции:
Решение вопроса о спецификации модели
2. Уравнение многофакторной регрессии, его построение и интерпретация
3. Система показателей тесноты многофакторной связи
4. Методика проведения анализа на основе построения уравнения многофакторной линейной регрессии
5. Предпосылки метода наименьших квадратов
Решение вопроса о спецификации модели
Множественная регрессия – уравнение связи с несколькими независимыми переменными:
Y=f(x1,x2,…,xp), (4.1)
где y - зависимая переменная (результативный признак);
x1,x2,…,xp – независимые переменные (факторы).
Для построения уравнения множественной регрессии чаще используются следующие функции:
линейная - y=a+b1·x1+b2·x2+…+bp·xp+ (4.2)
степенная ‑ y=a·x1b1·x2b2·…·xpbp · (4.3)
экспонентная - y=еa+b1·x1+b2·x2+…+bp·xp+ (4.4)
гипербола -
![]() (4.5)
(4.5)
Можно использовать и другие функции, приводимые к линейному виду.
Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также их совокупное влияние на моделируемый показатель. Построение модели начинают с решения вопроса о спецификации модели. Во множественной регрессии спецификация модели включает в себя решение двух вопросов:
отбор факторов
выбор вида уравнения.
Включение в уравнение множественной регрессии того или иного набора факторов связано, прежде всего, с представлением исследователя о природе взаимосвязи моделируемого показателя с другими жизненными явлениями.
Факторы включенные в модель должны отвечать следующим требованиям:
должны быть количественно измеримы. Если необходимо включать качественный фактор, то ему необходимо придать количественное определение.
не должны быть интеркоррелированны (т.е. факторные признаки не должны находится в тесной зависимости между собой и уж тем более, находится в точной функциональной связи). При включении в модель факторов с высокой интеркорреляцией (
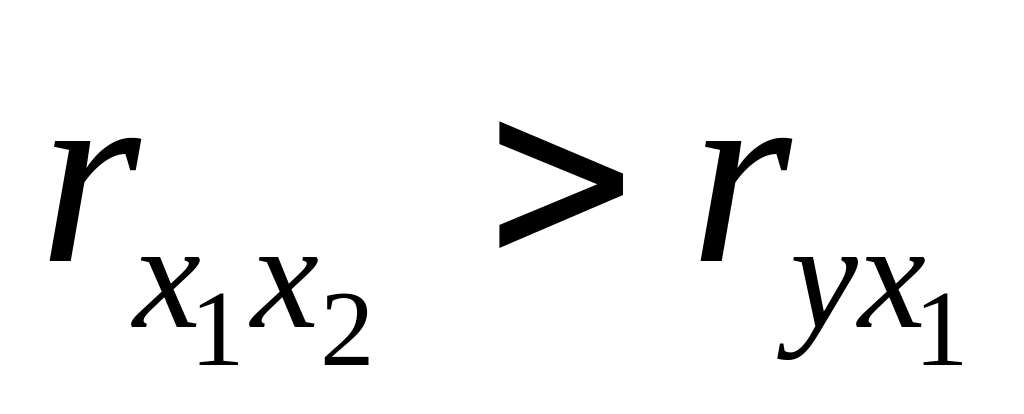 )
для множественной регрессии может
привести к нежелательным последствиям,
т.е. система норм уравнений может
оказаться плохо обусловленной и повлечь
за собой неустойчивость и ненадежность
оценок коэффициентов регрессии. Если
существует высокая корреляция между
факторами, то нельзя установить их
изолированное влияние на результативный
показатель, и параметры уравнения
регрессии окажутся не интерпретируемыми.
)
для множественной регрессии может
привести к нежелательным последствиям,
т.е. система норм уравнений может
оказаться плохо обусловленной и повлечь
за собой неустойчивость и ненадежность
оценок коэффициентов регрессии. Если
существует высокая корреляция между
факторами, то нельзя установить их
изолированное влияние на результативный
показатель, и параметры уравнения
регрессии окажутся не интерпретируемыми.
3. Факторы множественной регрессии должны объяснять вариацию зависимой переменной. Если строится модель с набором факторов P, то для нее рассчитывается показатель множественной детерминации R2, который фиксирует долю объяснений вариации результативного признака за счет рассмотрения в регрессии P - факторов. Влияние неучтенных факторов оценивается как 1 – R2 с соответствующей остаточной дисперсией.
При дополнительном включении в регрессию (P+1) – го фактора R2 должен возрастать, Docm уменьшаться. Если этого не происходит, и данные показатели мало отличаются друг от друга, то включенный в анализ (P+1) – фактор не улучшает модель и является практически лишним фактором.
Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии, но и приводит к статической незначимости параметров регрессии по t – критерию Стьюдента. Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически – в этом нет необходимости.
Отбор факторов производится на основе качественного теоретико-экономического анализа и проходит в 2 стадии: подбираются факторы, исходя из сущности проблемы, на основе матрицы показателей корреляции определяют t–статистики для параметров регрессии (чтобы исключить из модели коллинеарные факторы).
Поскольку одним из условий построения уравнения множественной регрессии является независимость действия факторов, то коллинеарность факторов нарушает это условие. Коллинеарность может возникать в силу различных причин. Например, несколько независимых переменных могут иметь общий временной тренд, относительно которого они совершают малые колебания.
Коэффициенты
интеркорреляции (т.е. корреляции между
факторными признаками) позволяют
исключить из модели факторы, дублирующие
друг друга. Считается, что 2 переменные
являются коллинеарными, т.е. находятся
между собой в линейной зависимости,
если коэффициент
![]()
Если факторы явно коллинеарны, то они дублируют друг друга и один из них необходимо исключить из модели.
Правило: предпочтение отдается не фактору, который более тесно связан с результатом, а тому фактору, который при достаточной связи с результатом имеет минимальную тесноту связи с другими факторами.
С целью выявления факта коллинеарности факторов составляется матрица парных коэффициентов корреляции, измеряющих тесноту связи каждого из факторов-признаков с результатом и между собой.
Таблица 4.1. – Матрица парных коэффициентов корреляции
Признак |
У |
Х1 |
… |
Хm |
У |
1 |
ryx1 |
… |
ryxm |
Х1 |
ryx1 |
1 |
… |
rx1xm |
… |
… |
… |
… |
… |
Хm |
ryxm |
rx1xm |
… |
1 |
Пример.
Изучается зависимость
![]()
Построим матрицу парных коэффициентов корреляции
Признак |
y |
x |
z |
v |
y |
1 |
|
|
|
x |
0,9 |
1 |
|
|
z |
0,8 |
0,9 |
1 |
|
v |
0,7 |
0,6 |
0,3 |
1 |
В модели оставляем
фактор Z,
т.к. несмотря на то, что коэффициенты
парной корреляции
![]() ,
но зато связь фактора z
с другим фактором слабее:
,
но зато связь фактора z
с другим фактором слабее:
![]()
По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. наблюдается совокупность воздействия факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценивать влияние каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка параметров с помощью МНК.
Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий:
затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов «в чистом» виде, т.к. факторы коррелированны. Параметры линейной регрессии теряют экономический смысл.
оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняют с изменением объема наблюдений не только по величине, но и по знаку, что делает модель непригодной для анализа и прогнозирования.
Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов. Сравнивая между собой коэффициенты множественной детерминации факторов можно выделить переменные, ответственные за мультиколлинеарность, а следовательно, решать проблему отбора факторов, оставляя в модели факторы и минимальной величиной коэффициента множественной детерминации.
Способы определения наличия или отсутствия мультиколлинеарности
Анализ матрицы коэффициентов парной корреляции: факторы xi и xj могут быть признаны коллинеарными, если
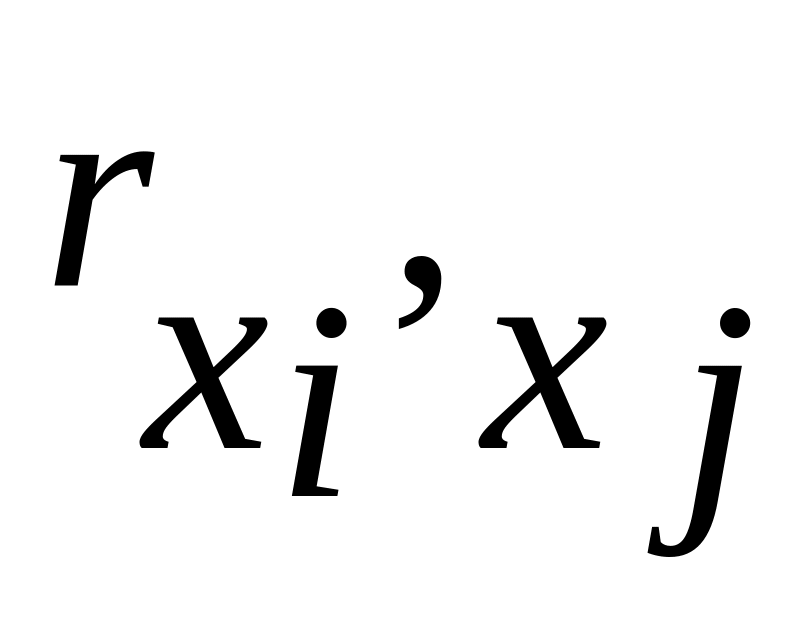 >0,8
>0,8Исследование матрицы
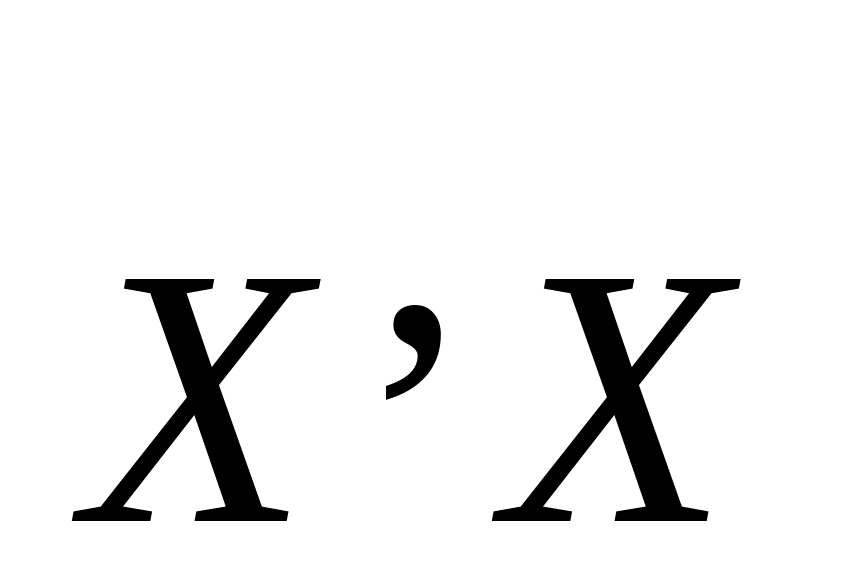 :
если определитель матрицы
близок к нулю, то это свидетельствует
о наличии мультиколлинеарности.
:
если определитель матрицы
близок к нулю, то это свидетельствует
о наличии мультиколлинеарности.
Установление мультиколлинеарности возможно посредством исключения из корреляционной модели одного или нескольких линейно связанных факторных признаков или преобразование исходных факторных признаков в новые, укрупненные факторы. Вопрос о том, какой из факторов следует отбросить, решается на основе качественного и логического анализа изучаемого явления.