Теорема Шеффе

Следующая теорема показывает, что из поточечной сходимости плотностей следует сходимость соответствующих им мер по вариации

Теорема Шеффе

Пусть - вероятностные меры, абсолютно непрерывные относительно мерыи- соответствующие плотности меротносительно меры

Тогда, если , то

Доказательство этой теоремы проведите самостоятельно по схеме доказательства соответствующего утверждения в теореме Пуассона с использованием теоремы Лебега о мажорированной сходимости.

Сглаживание распределений

Примером последовательности случайных величин, сходящихся в среднеквадратическом к нулю является последовательность

Так как

,

то для любой случайной величины и, следовательно,во всех точках непрерывности функции распределения. Так как , нормальное распределение имеет плотность, то случайная величинатоже имеет плотность даже для разрывной функции распределенияи ее функция распределения при больших n является гладким приближением функции распределения.

Характеристические функции случайных величин и их распределений

В данном разделе вводится определение характеристической функции случайной величины. Эти функции являются основным инструментом доказательства теорем о слабой сходимости в классической теории вероятностей.

Математическое ожидание комплекснозначной функции от случайной величины

Пусть - случайная величина и- комплекснозначная функция

.

Тогда математическое ожидание

Определение характеристической функции

Пусть - случайная величина. Характеристической функцией случайной величиныназывается функциядействительного аргумента t

Свойства характеристической функции

Очевидные свойства характеристической функции приведем без доказательства

1. Характеристическая функция существует для любой случайной величины

2. 

3. 

4. равномерно непрерывна. Действительнопо теореме Лебега о мажорируемой сходимости.

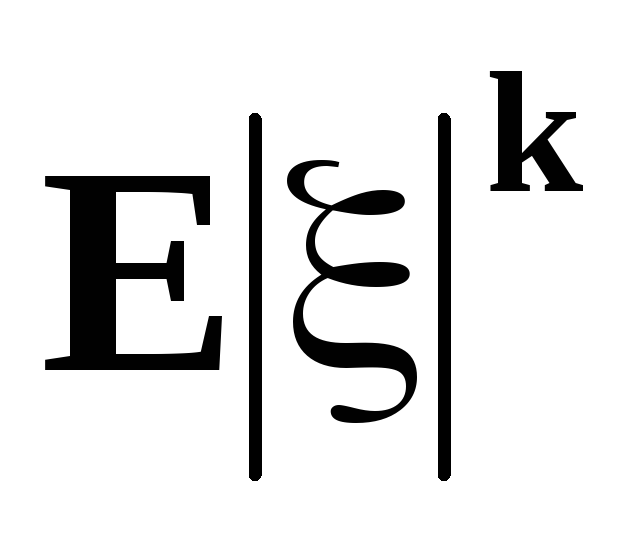5. Если существуетдля некоторого k=1,2,..., то существует ипричем. Для доказательства достаточно продифференцировать необходимое количество раз интеграл, определяющий характеристическую функцию, по параметру t.

6. 

7. Пустьи- две независимые случайные величины, тогда. Это следует их того, что математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.

8. Если - плотность случайной величины, то- является преобразованием Фурье плотности. Подробно свойства преобразования Фурье рассматриваются в курсе математического анализа.

Преобразование Лапласа и производящая функция

Если случайная величина неотрицательна, то для любого неотрицательного sвсегда существует

которое называется преобразование Лапласа распределения случайной величины .

Если случайная величина неотрицательна и целочисленна, то для любого z такого, чтовсегда существует

которое называется производящей функцией случайной величины

Заменой переменных эти преобразования можно выразить через характеристическую функцию.

Теорема единственности для характеристических функций и характеристические функции важных распределений

Соответствие между функциями распределения и характеристическими функциями является взаимнооднозначным. Каждой функции распределения соответствует одна и только одна характеристическая функция. Это свойство позволяет использовать характеристические функции для различения и определения распределений случайных величин. Прежде чем доказывать теорему единственности, подсчитаем характеристические функции наиболее важных распределений.

Название распределения	Характеристическая функция
Вырожденное в точке a
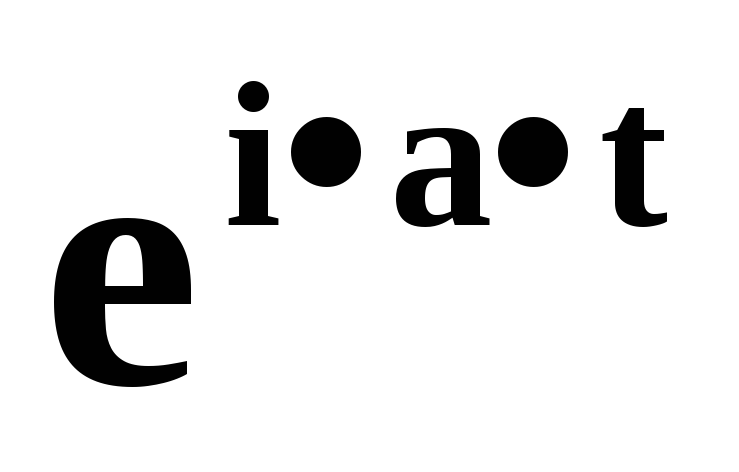
Биномиальное (n,p)
Геометрическое p
Пуассоновское
Нормальное стандартное
Нормальное
Равномерное на отрезке (0,1)
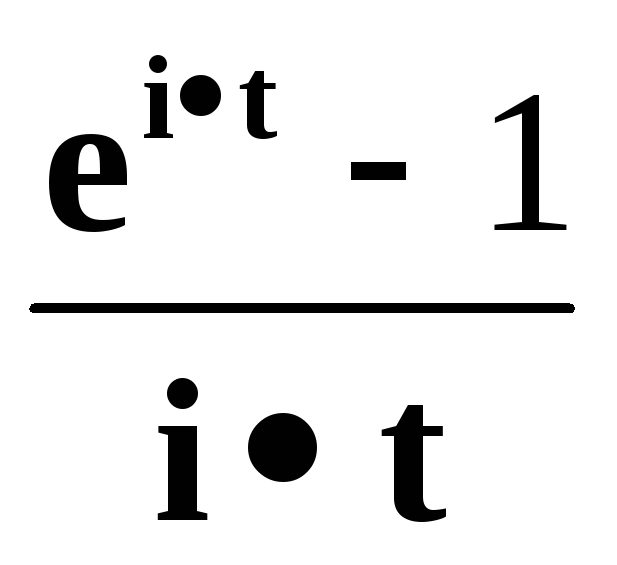
Равномерное на отрезке (a,b)
Бета
Экспоненциальное
Гамма

Заметим, что плотность и характеристическая функция стандартной нормальной случайной величины отличаются лишь множителем. Это позволяет нам доказать следующее важное равенство.

Равенство Парсеваля.

Пусть - случайная величина с функцией распределенияи характеристической функцией,

.

Тогда плотность случайной величины можно представить в виде

.

Доказательство.

Пусть

Рассмотрим очевидное равенство

умножим его на плотность случайной величины и проинтегрируем поt от до . Учитывая, что

получим требуемое утверждение

Доказательство завершено.

Меняя в доказательстве местами случайные величины иполучаем следующий вариант равенства Парсеваля

Очевидно, приведенные формулы справедливы и для несобственных функций распределения.

Теорема единственности для характеристических функций.

Соответствие между функциями распределения и характеристическими функциями является взаимнооднозначным.

Доказательство.

Интегрируя равенство

по отрезку [A,B], получаем

Левая часть этого равенства стремится к

,

а правая полностью зависит от . Таким образом функция распределенияопределяется пооднозначно.

Теорема доказана.

Формула

называется формулой обращения для характеристических функций.

Теорема непрерывности для характеристических функций

Важность характеристических функций для теории вероятностей определяется тем , что сходимость последовательности характеристических функций влечет за собой слабую сходимость последовательности соответствующих функций распределения.

Для того, чтобы это доказать, необходимо использовать следующую лемму и теорему.

Лемма о выборе.

Пусть - произвольная последовательность ограниченных в совокупности функций, заданных на прямой и- последовательность действительных чисел. Тогда существует подпоследовательность функцийкоторая сходится во всех точкахк некоторой предельной функции.

Доказательство.

Для доказательства теорем применим диагональный метод Кантора.

Из курса математического анализа известно, что любая ограниченная числовая последовательность имеет сходящуюся подпоследовательность. Последовательность следовательно, как ограниченная последовательность, имеет сходящуюся подпоследовательность. Из этой подпоследовательности выберем другую, сходящуюся в точке-и т.д. Тогда диагональная последовательностьсходится во всех точках

Доказательство закончено.

Выбрав в качестве множества точек множество рациональных чисел и учитывая что, функцию распределения достаточно задать лишь на всюду плотном множестве получаем следующую теорему.

Теорема о выборе.

Пусть - произвольная последовательность функций распределения. Тогда существует подпоследовательность последовательности, которая сходится во всех точках непрерывности к некоторой предельной неубывающей непрерывной слева функции.

Заметим, что функция не обязательно является функцией распределения, но (очевидно) обязательно является неубывающей функцией, такой что

(несобственной функцией распределения).

Например, последовательность функций распределения случайных величинсходится прик функции

Теорема непрерывности для характеристических функций.

Для того, чтобы

необходимо и достаточно, чтобы для всех t

Доказательство.

Пусть Тогда используя ограниченность, непрерывность поxдля любогоtфункциии теорему Хелли-Брея получаем

Доказательство необходимости завершено.

Пусть теперь Тогда, используя теорему о выборе, мы можем извлечь из любой подпоследовательности последовательности функций распределенияслучайных величин, сходящуюся к некоторой функцииподпоследовательность, при этом соответствующая подпоследовательность характеристических функцийкак подпоследовательность сходящейся последовательности характеристических функций сходится к. Покажем, что функцияявляется функцией распределения.

Полагая

и применяя к паре функций ,равенство Парсеваля

получаем, что, с одной стороны, для любого x

С другой стороны, для любых N,n и х

Таким образом:

1. Функция является собственной функцией распределения

2. Из любой подпоследовательности последовательности функций распределения случайных величинможно извлечь сходящуюся кподпоследовательность

3. Характеристическая функция совпадает с

Используя теорему единственности для характеристических функций получаем из 1) и 3), что функции исовпадают и из 2) следует утверждение второй части теоремы (доказательство от противного).

Доказательство завершено.