Условная вероятность

Часто случайные компоненты в опыте и соответственно координаты элементарного исхода являются зависимыми. В этом случае для определения распределения используют понятие условной вероятности.

Урновая схема

Рассмотрим, например, эксперимент, описывающий выбор двух шаров из урны, содержащей 20 черных и 10 белых шаров, без возвращения. Элементарным исходом будет вектор

из нулей и единиц (1 – черный шар, 0 - белый), где первая координата описывает цвет второго извлеченного шара, а вторая цвет первого извлеченного шара.

Как задать вероятность элементарного исхода?

Ясно, что событие «На первом шаге вынут черный шар» должно иметь вероятность

Ясно также, что если бы мы знали цвет извлеченного на первом шаге шара, то точно также могли бы определить вероятность извлечения черного шара на втором шаге. Именно, если первый шар белый, то (при этом условии) вероятность извлечь черный шар на втором шаге равна

Если первый шар черный, то

Тогда естественно определить вероятность исхода (1,1) так чтобы выполнялась формула условной вероятности

т.е.

и

Аналогично определяются вероятности остальных элементарных исходов

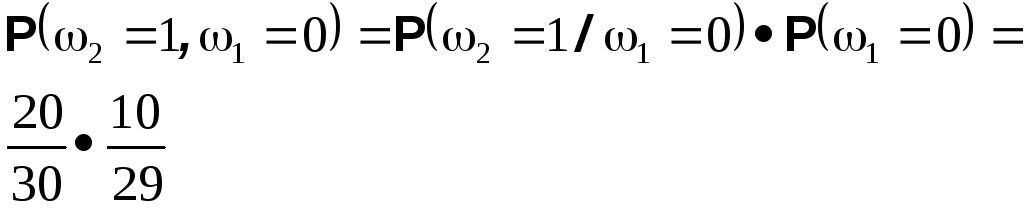
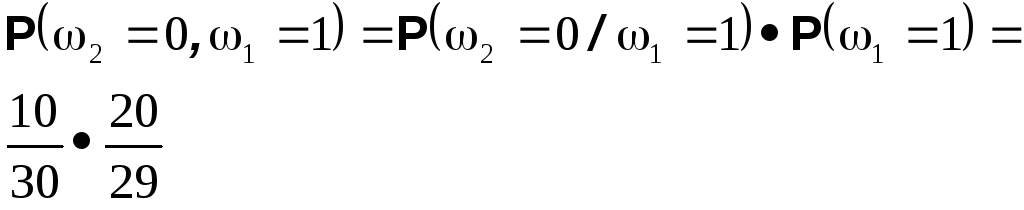
Теперь нетрудно, например, вычислить вероятность того, что второй извлеченный шар будет черным. Она равна

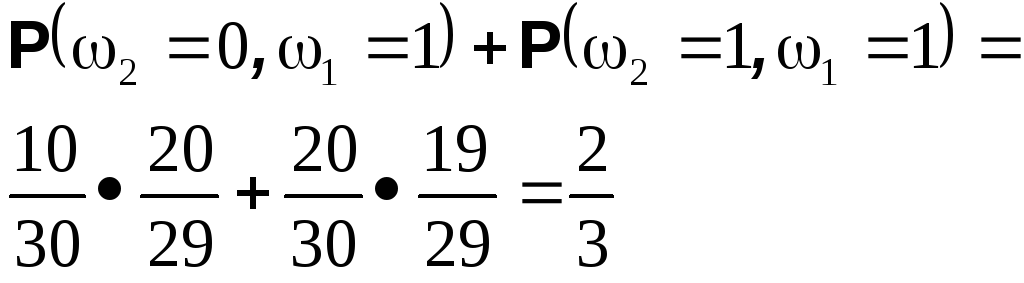
Покажите, что нас самом деле вероятность вытащить черный шар одинакова не только для первого и второго, но и для любого другого шага выбора (пока она не станет равной, естественно, нулю – когда кончатся черные шары)

Заметим, что данный результат в применении к задаче о студенте на экзамене означает, что студенту все равно каким идти – первым или вторым.

Марковская зависимость

Легко распространить изложенное выше на случай элементарного исхода с n целочисленными координатами.

Особенно просто записывается вероятность элементарного исхода когда имеет место марковская зависимостькоординат, т.е. когда распределение следующей координаты зависит только от значения предыдущей координаты

В этом случае последовательные переходы от координаты к координатеи т.д. называются шагами ,а вероятности

называются переходными вероятностями (за один шаг).

Если каждая координата вектора принимает значения в одном и том же конечном множестве(множестве состояний) и переходные вероятности не зависят отn, то последовательность называетсяконечной цепью Маркова. В этом случае вероятность элементарного исхода можно записать так

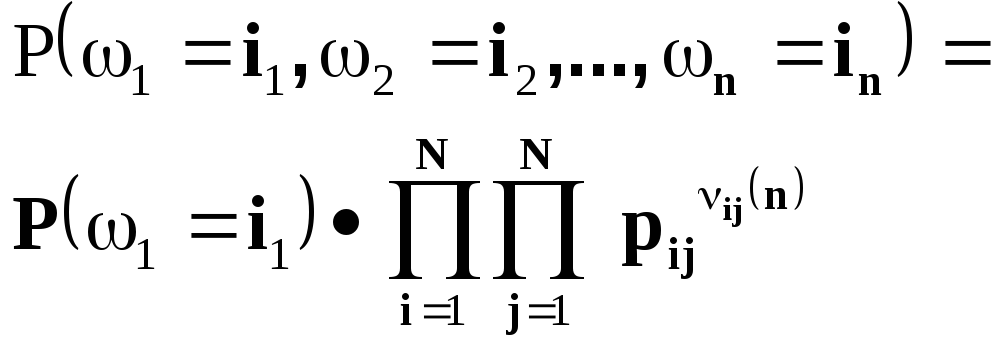
где

- количество переходов из состояния iв состояние j

Подробно марковские зависимости исследуются в теории случайных процессов.

Формула полной вероятности и формула Байеса

Часто при решении простых задач теории вероятностей формально не вводят вероятностное пространство, а сразу выделяют полную группу случайных событий (условий), вероятности которых легко определить из условий задачи и вероятность интересующего события находят по формуле полной вероятности

Например, рассмотрим следующую задачу.

• В ящике содержатся детали, поступившие с трех разных заводов.

• Доля брака среди деталей первого завода – 0,1, второго - 0,2, третьего - 0,4.

• Количество деталей первого завода в ящике - 20, второго –30, третьего – 50. Найти вероятность того, что наудачу выбранная из ящика деталь окажется бракованной (событие A).

• Решение. При формальном определении, в качестве элементарного исхода следует взять вектор с двумя координатами. Первая указывет номер завода, с которого поступила наудачу выбранная деталь, вторая - бракована эта деталь или нет. Далее действуя в духе предыдущего пункта легко определить вероятности всех элементарных исходов и соответственно, вероятность любого события A по формуле

• 

• С другой стороны обозначив B₁,B₂, B_{3 –} события, заключающиеся в том, что деталь поступила, соотвественно, с первого, второго, третьего завода, и применив формулу полной вероятности, получим

• 

Различие в двух подходах к решению данной задачи состоит в том , что в первом случае полностью определяется вероятностное пространство и можно найти вероятность любого события по одной и той же формуле, во втором модель полностью не строится и мы (по-существу) определяем вероятности только тех элементарных исходов, которые входят в интересующее нас событие.

С формулой полной вероятности тесно связана формула Байеса.

Она позволяет найти, как, иногда, говорят инженеры, обратные вероятности, т. е. вероятности событий полной группы при условии, что произошло событие A.

Например, пусть в условиях предыдущей задачи известо, что из ящика извлечена бракованная деталь и требуется найти вероятность того, что она выпущена вторым заводом. Тогда по формуле Байеса имеем

Заметим, однако принципиальную разницу этих формул. Формула полной вероятности является просто следствием свойства счетной аддитивности вероятности и ее применение часто означает, что мы неявно строим вероятностное пространство. Формула Байеса действительно расчетная – для ее применения требуется , чтобы вероятностное пространство уже было определено.