Гамма-распределение.

Рассмотрим плотность

где

параметры распределения. Распределение с такой плотностью называется гамма распределение. Приведем график плотности этого распределения при

Величина

рассматриваемая как функция переменной

называется гамма-функцией и имеет следующие, легко доказываемые свойства

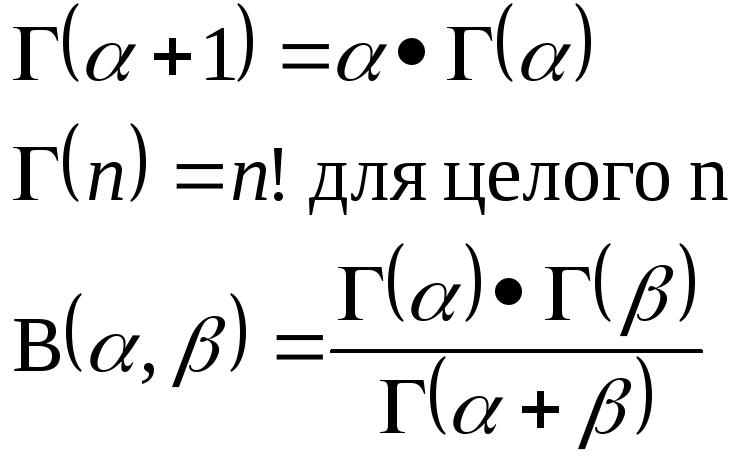
Это распределение обозначается

Гамма распределение обобщает экспоненциальное распределение и превращается в него при

Гамма распределение с целым параметром

называется распределение Эрлангапорядкаи обозначается

Распределение

где n – целое, называется распределение хи-квадрати обозначается

Построение меры в конечномерном пространстве Борелевская сигма-алгебра в конечномерном пространстве

Борелевская сигма-алгебра на пространстве действительных векторов определяется аналогично борелевской сигма-алгебре на прямой с заменой прямоугольников

на параллелепипеды

Обозначим ее

Эта сигма-алгебра содержит все практически важные множества векторов. Множество, принадлежащее борелевской сигма-алгебре называется борелевское множество.

Определение случайного вектора

Пусть

основное вероятностное пространство

пространство векторов с борелевской сигма-алгеброй

Покажите, что координаты случайного вектора – случайные величины и, наоборот, вектор, составленный из случайных величин – случайный вектор

поточечное измеримое отображение, ставящее в соответствие каждому элементарному исходу основного пространства действительный вектор. Это отображение называется случайный вектор.

Вероятностная мера, определенная на борелевской сигма-алгебре по формуле

называется распределением случайного вектора.

Пусть

случайный вектор и

Функция

называется функция распределения (иначе - совместная функция распределения) случайного вектора

Аналогично одномерному случаю определяются дискретные и непрерывные случайные вектора и их распределения.

Плотность распределения случайного вектора f(x) – это функция, удовлетворяющая условию

Мера Лебега в конечномерном пространстве

Мера Лебега в конечномерном пространстве это мера, приписывающая параллелепипеду его объем. В частности, мера Лебега прямоугольника это его площадь.

Мера Лебега на квадрате - Задача о встрече

Рассмотрим следующую задачу.

Два человека договорились встретиться в определенном месте в течение часа и ждать друг друга не более 10 минут. Найти вероятность, того они встретятся, если момент прихода каждого совершенно случаен.

Для решения задачи построим следующую вероятностную модель. Исходом опыта является вектор

где первая координата – момент прихода первого человека, вторая – момент прихода второго. Сигма-алгебра – все борелевские подмножества единичного (1 час=1 единица времени) квадрата. Предположение о совершенной случайности моментов прихода приводит к вероятностной мере, которая приписывает каждому множеству единичного квадрата его площадь. Эта мера называется мера Лебега на квадрате. Подсчитаем вероятность интересующего нас события. Два человека встретятся, если

Площадь этой наклонной полосы

равна

Независимые случайные величины

Случайные величины

,

заданные на одном вероятностном пространстве, называются независимыми, если для любых борелевских множеств

В одну сторону доказательство очевидно

Можно показать, что независимость случайных величин эквивалентна тому, что их совместная функция распределения равна произведению их одномерных функций распределения

Это важно. Докажите!

Если случайные величины независимы и имеют совместную плотность, то она является произведением их одномерных плотностей. Верно и обратное.