Пуассоновское распределение - теорема Пуассона
Пусть
некоторый параметр.
Распределение на пространстве неотрицательных целых чисел называется пуассоновское распределение (распределение Пуассона), если
Распределение Пуассона является предельным случаем биномиального распределения при специальном поведении параметров (n,p) биномиального распределения Это будет показано в дальнейшем. Заметим, что биномиальное распределение можно рассматривать как распределение на пространстве неотрицательных целых чисел, положив
Определим на сигма-алгебре всех подмножеств неотрицательных целых чисел две вероятности P и Pn ,, соответствующие пуассоновскому и биномиальному распределениям :
Теорема Пуассона.
Пусть параметры биномиального распределения изменяются следующим образом
Тогда
т.е. биномиальная вероятность равномерно по всем случайным событиям стремится к пуассоновской вероятности.
Доказательство.
Докажем вначале, что в условиях теоремы для любого фиксированного k
Действительно, сгруппировав множители входящие в pk,n следующим образом
получим
Покажем теперь, что из сходимости
следует
сходимость
Действительно, определив множество A* следующим образом
получим
Далее, так как на множестве A*
для любого N получаем
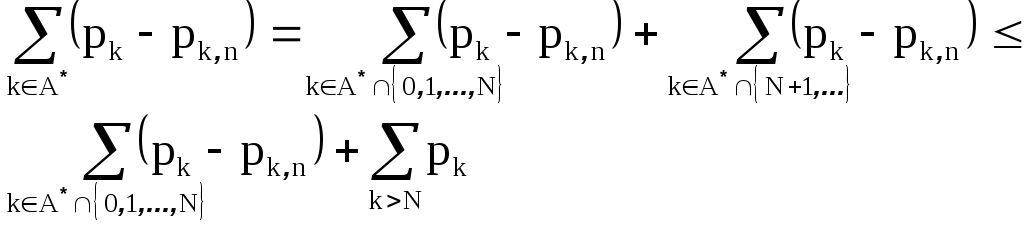
Выбрав N достаточно большим, можно сделать вторую сумму сколь угодно малой, первую сумму после этого можно сделать также сколь угодно малой выбрав достаточно большое n.
Доказательство завершено.
При больших k рассчитать пуассоновскую вероятность гораздо легче, биномиальную. Пуассоновское распределение используется для приближения биномиального распределения в тех случаях, когда количество испытаний в схеме Бернулли велико, а вероятность успеха мала.
Сходимость по вариации - приближение одних моделей другими
Предположим задано некоторое пространство элементарных исходов и сигма-алгебра событий.
Определив на сигма-алгебре две вероятности P и Q,, получим два вероятностных пространства и соответственно две математические модели описывающие один и тот же эксперимент. Естественно считать эти модели совпадающими, если они дают одинаковые вероятности для всех случайных событий
Две модели естественно считать близкими (приближающими друг друга) если этот супремум достаточно мал.
Дадим следующее определение.
Сходимость по вариации.
Последовательность вероятностей (вероятностных мер или их распределений) Pnсходится к вероятности (распределению) P по вариации, если
В предыдущем пункте мы доказали сходимость по вариации биномиальной вероятности к пуассоновской (в некоторых условиях).
Измеримое пространство.
В предыдущем пункте мы определили две различные вероятности на одной и той же сигма-алгебре событий. В дальнейшем нам придется делать это неодократно. Для удобства дадим следующее определение.
Измеримое пространство – это пара
Независимость событий и условная вероятность. Построение моделей.
При построении дискретных вероятностных моделей достаточно определить распределение на множестве элементарных исходов. Для того, чтобы определить вероятяность элементарного исхода часто используют понятие независимости и понятие условной вероятности.
Независимость
Различие между независимостью попарно и в совокупности. Пример Бернштейна
Данный пример показывает, что существуют попарно независимые события , которые не являются независимыми в совокупности.
Рассмотрим тетраэдр, грани которого покрашены в три цвета следующим образом:
1 грань – синяя
2 грань – зеленая
3 грань – желтая
4 грань разделена на три сектора – синий, зеленый и желтый.
Опыт состоит в бросании тетраэдра и наблюдении цвета выпавшей (нижней) грани.
Обозначим события
A– на грани есть синий цвет
B– на грани есть зеленый цвет
C– на грани есть желтый цвет
Тогда, используя симетричность тетраэдра и классическую вероятностную модель получим:
Для исключения неоднозначности при интерпретации понятия независимости в теории вероятностей при построении моделей используется, в основном, независимость в совокупности, как более сильная. В дальнейшем говоря о независимости мы, если не указано противное, будем подразумевать независимость в совокупности.