Первоначальное распределение поставок методом учета наименьших затрат

Заполнение начинается с клеток, имеющих минимальный тариф.

Пример 4. распределить поставки с учетом наименьших затрат по условию примера 3.

1. Составим таблицу.

Распределим поставки с учетом наименьших затрат.

Выберем клетки с наименьшими тарифами. Такими клетками являются – одна клетка (3; 3), с тарифом 1. Заполним ее поставкой: . Так как спрос третьего потребителя удовлетворен, то клетки (1; 3) и (2; 3) мысленно вычеркиваем. У третьего поставщика осталось 10 единиц груза. Далее выбираем клетки с тарифами 2. Таковыми являются клетки (1; 2) и (3; 1). Поставки: в клетку (1; 2): ; в клетку (3; 1): . Спрос второго потребителя выполнен, значит, мысленно вычеркиваем клетки (2; 2) и (2; 3). Мощности первого и третьего поставщиков изъяты полностью, значит, мысленно вычеркиваем клетки (1; 1), (1; 4) и (3; 4). Далее выбираем клетку (2; 1) с оставшимся наименьшим тарифом в 4 - . Спрос первого потребителя удовлетворен, у второго поставщика осталось еще 40 единиц груза. Невычеркнутой осталась клетка (2; 4) с тарифом 7. В нее заполним поставку четвертому потребителю от второго поставщика - .

Потребители Поставщики	В1	В2	В3	В4
	50	70	40	40
А1 – 70	5 -	2 70	3 -	6 -
А2 – 80	4 40	3 0	5 -	7 40
А3 – 50	2 10	4 -	1 40	5 -

Сделаем проверку условий.

1. Баланс сохранен.

2. Число заполненных клеток: 5 – условие не выполнено. В этом случае в произвольную клетку, например, (2;2) дадим поставку равную 0. Тогда число заполненных клеток поставками будет равно 6, то есть столько, сколько должно быть.

Ответ: опорный план

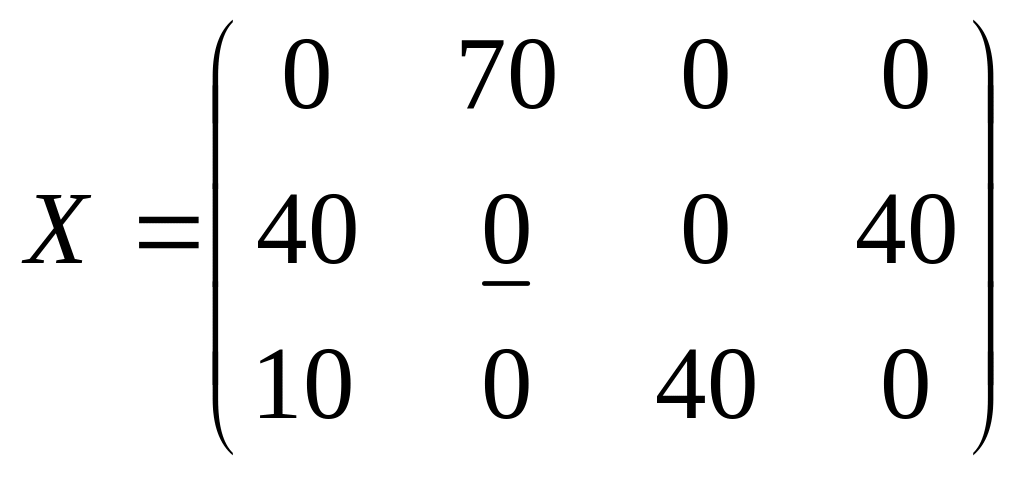
Нахождение оптимального плана распределения поставок методом потенциалов

Метод потенциалов служит для определения оптимальности полученного распределения поставок. Потенциалы – это числа V_i и U_j.

Потенциалы вводят для поставщиков: V_i и для потребителей: U_j. Всего потенциалов будет m+n.

Для вычисления значений потенциалов используется понятие оценка клетки.

Оценка клетки это сумма потенциала поставщика, потенциала потребителя и тарифа.

Потенциалы находятся из условия: оценка заполненной клетки равна нулю.

Для нахождения значений потенциалов дополняют таблицу 1 горизонтальной строкой снизу для U_j и вертикальным столбцом справа - для V_i. Так как количество потенциалов , а число заполненных клеток , то одно значение U_j или V_i берут равным нулю. Выбирают то, против которого наибольшее число заполненных клеток.

Продемонстрируем решение по условию примера 3.

Построим таблицу.

Bj Ai	В1	В2	В3	В4	Vi
	50	70	40	40
А1 – 70	5 50	2 20	3 (-1)	6 (-2)	0
А2 – 80	4 (-2)	3 50	5 30	7 (-2)	-1
А3 – 50	2 (0)	4 (5)	1 10	5 40	3
Uj	-5	-2	-4	-8

Положим значение V₁ равными нулю, т.е. . Тогда согласно выше указанному условию, найдем оценку заполненной клетки (1; 1):

отсюда U₁ = -5,

оценка заполненной клетки (1; 2) равна:

отсюда U₂ = -2.

Аналогично находят значения остальных потенциалов:

По найденным потенциалам находят оценки свободных клеток по формуле:

.

Эти оценки могут иметь значения меньше нуля, равны нулю или больше нуля. Оценки свободных клеток записаны в таблицу в скобках.

Проверяем критерий оптимальности: опорный план оптимальный, если оценки всех свободных клеток неотрицательны.

Опорный план, построенный по методу «Северо-западного угла» не является оптимальным, так как есть оценки клеток меньше нуля. Для получения оптимального плана следует выполнить перераспределение поставок. Для этого строят цикл для клетки с наименьшей отрицательной оценкой.

Циклом называется замкнутый многоугольник, стороны которого вертикальные или горизонтальные отрезки; одна вершина, для которой строится цикл, свободна, а все остальные вершины – заполнены поставками.

Вершине, для которой строится цикл, присваивается номер 1, а остальные нумеруются порядковыми числами 2, 3 и так далее по часовой или против часовой стрелки. По построенному циклу перемещаем минимальный груз из четных клеток в нечетные.

Полученное распределение поставок заносим во вновь построенную таблицу. И так до тех пор, пока не получим оптимальное распределение поставок, то есть пока оценки всех клеток получатся неотрицательными.