Транспортная задача (тз)

Простейшими ТЗ являются задачи о перевозках некоторого однородного груза из пунктов отправления в пункты назначения, или от поставщиков к потребителям, при обеспечении минимальных затрат на перевозки. Как правило, начальные условия таких задач записываются в таблицу. Для m поставщиков и n потребителей таблица имеет вид:

Мощность поставщиков	Спрос потребителей
	N1	N2	---	Nn
	c11 x11	c12 x12	---	c1n x1n
	c21 x21	c22 x22	---	c2n x2n
---	---	---	---	---
	cm1 xm1	cm2 xm2	---	cmn xmn

Показатели c_ij означают затраты на перевозку единицы груза от i-го поставщика к j-му потребителю ( i = 1; 2; ...; m; j = 1; 2; ...; n);

M_i - мощность (предложение) i- го поставщика;

N_j - спрос j - го потребителя;

x_ij - поставка (количество груза), от i-го поставщика к j-му потребителю.

Суммарные затраты на перевозку всего груза выражаются целевой функцией

Если суммарная мощность поставщиков (предложение) равна суммарному спросу потребителей, то соответствующая модель ТЗ называется закрытой.

,

Если 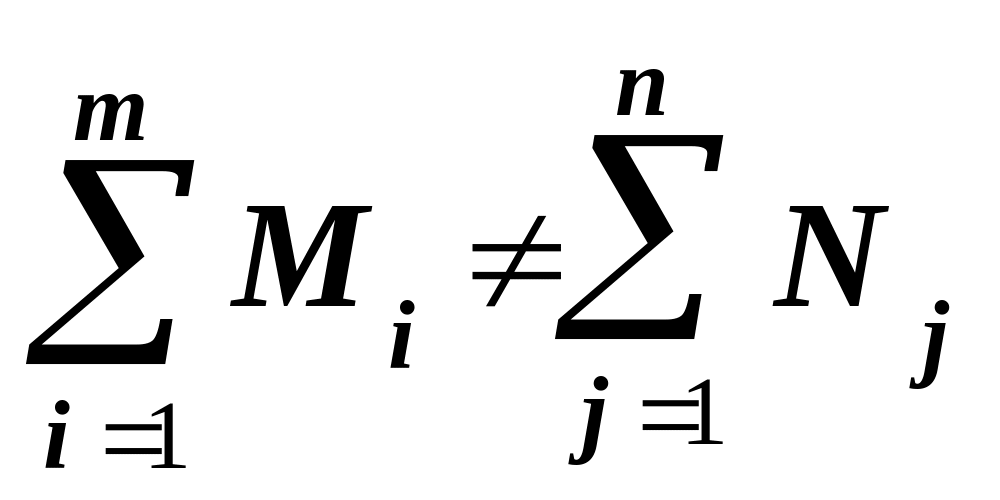, то модель ТЗ называется открытой.

Алгоритм решения тз

1. Определяют модель ТЗ.

Если модель ТЗ открытая, то в случае

(объем мощностей поставщиков превышает объем спроса потребителей) вводят фиктивного потребителя ФN со спросом равным разности

Если (объем спроса потребителей превышает объем мощностей поставщиков), то вводят фиктивного поставщика ФМ с мощностью равной разности

Затраты на перевозки к ФN или ФМ считают равными нулю (или произвольными, но одинаковыми).

2. Составляют первоначальный план распределения поставок по методу «северо-западного угла» или методу учета наименьших затрат.

При этом должно быть заполнено клеток.

Если число заполненных клеток окажется меньше этого числа, то недостающее число свободных клеток заполняют нулевыми поставками.

3. Полученное распределение поставок оценивают методом потенциалов.

При этом если все оценки клеток окажутся неотрицательные, то полученное распределение является оптимальным.

Тогда подсчитывают суммарные затраты на перевозки.

Если хотя бы одна оценка клетки окажется отрицательной, то полученное распределение не является оптимальным.

4. Для получения нового, улучшенного распределения поставок нужно построить цикл для клетки, которая имеет наибольшую по абсолютной величине отрицательную оценку. По циклу перемещают наименьшую поставку среди четных клеток цикла. В результате перераспределения поставок клетка, для которой строился цикл, получает поставку, а четная клетка, которой соответствовала наименьшая поставка, освобождается.

5. Полученное распределение поставок опять проверяют на оптимальность методом потенциалов.

6. Процесс улучшения распределения поставок продолжают до тех пор, пока получат оптимальное распределение поставок. Признаком оптимального распределения поставок служит наличие неотрицательных оценок всех клеток этого распределения.

7. Если среди оценок клеток последнего оптимального распределения есть хотя бы одна нулевая для свободной клетки, то оптимальное распределение поставок не является единственным.

8. Для полученного оптимального распределения вычисляют суммарные затраты на перевозки как сумму произведений затрат на соответствующие поставки.