Основные теоремы линейного программирования

Теорема 1.Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым..

Теорема 2.Если существует и притом единственное оптимальное решение задачи линейного программирования то оно совпадает с одной из угловых точек множества допустимых решений..

Теорема 3.Каждому допустимому базисному решению задачи ЛП соответствует угловая точка области допустимых решений системы ограничений.

Теорема 4.Каждой угловой точке множества допустимых решений системы ограничений соответствует допустимое базисное решение.

Графический метод решения задачи линейного программирования

Если задача линейного программирования содержит только две переменные, то ее можно решить геометрическим (графоаналитическим) методом. Этот метод основан на следующих положениях.

I. Областью решений неравенства является полуплоскость, расположенная выше или ниже прямой, описываемой уравнением .

Если задана система линейных неравенств с двумя переменными:

то областью ее решений будет служить выпуклый многоугольник, образованный пересечением полуплоскостей, соответствующих области решения каждого неравенства системы.

Заметим, что область решений системы неравенств может быть и неограниченной; и пустой, когда система неравенств противоречива.

Пример 1. Найти область решений неравенства

.

Построим прямую

-5

2

0

х

у

на плоскости оху. Для этого найдем точки пересечения прямой с осями: имеем при ; при .

Решением уравнения являются точки, принадлежащие этой прямой. Теперь рассмотрим строгое неравенство

.

Для того чтобы выяснить, какая полуплоскость служит областью решения этого неравенства, решим его относительно переменной у:

.

Отсюда следует, что областью решения неравенства является полуплоскость, расположенная ниже прямой (показано штрихами вниз).

Другой способ нахождения области решения неравенства заключается в использовании контрольной точки. Обычно за нее берется начало координат. Подставляя и в неравенство, получим . Так как полученное выражение справедливо, то точка с координатами (0,0) включается в область решения неравенства и, следовательно, искомой областью решения служит полуплоскость ниже прямой, включая и прямую.

II. Если задача линейного программирования имеет оптимальное решение, то целевая функция принимает оптимальное значение в одной из угловых точек многоугольника решений.

Каким образом найти эту точку покажем на примере 2.

Пример 2. Определить экстремумы функции

при системе ограничений:

Решение.

В системе координат построим прямые соответствующие уравнениям.

Найдем область решения каждого неравенства.

М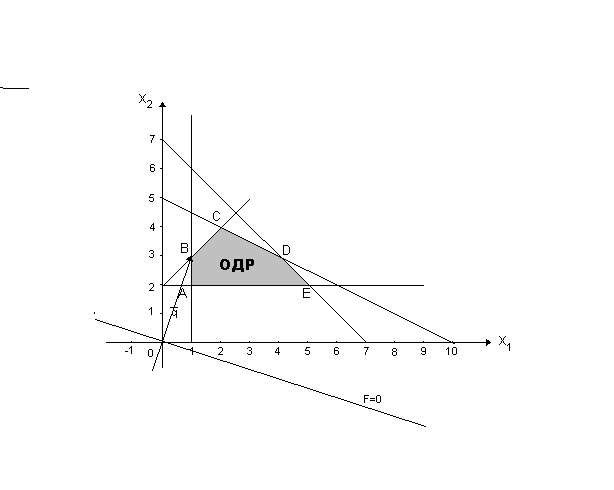 ногоугольник АВСDЕ, образованный пересечением всех полуплоскостей, образует область допустимых решений системы неравенств.

Далее на этой же плоскости построим вектор .

Координаты вектора равны коэффициентам при переменных в целевой функции . Полагая F=0, построим соответствующую прямую или .

Будем перемещать эту прямую параллельно самой себе в направлении вектора (т.е. снизу вверх) до тех пор, пока прямая не выйдет из ОДР. Зафиксируем ту вершину многоугольника АВСDЕ, через которую F = 0 выходит из ОДР. Такой вершиной является С.

Определим ее координаты. Для этого решим систему уравнений двух прямых, на пересечении которых находится точка С

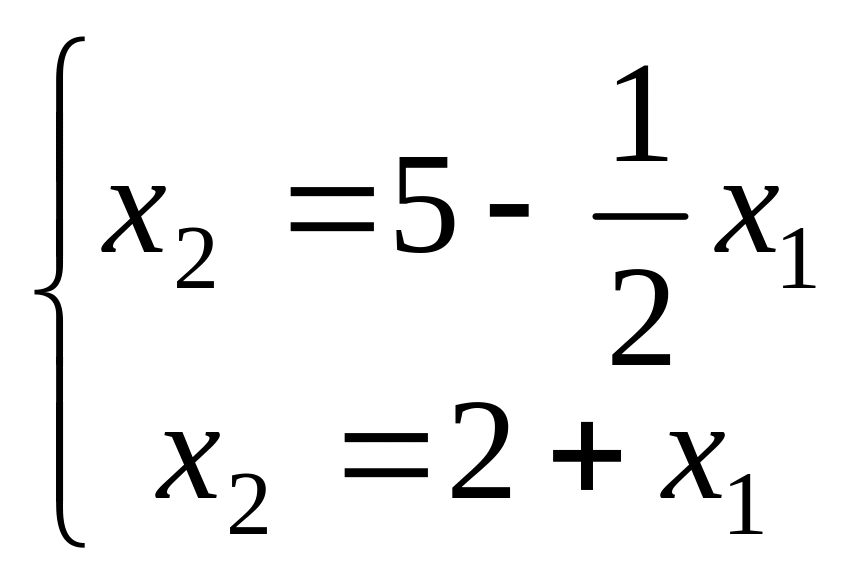
Подставим координаты т. С (2; 4) в уравнение целевой функции F. Вычислим значение .

Чтобы определить минимум целевой функции F будем перемещать прямую F=0 параллельно самой себе в направлении противоположном вектору . Зафиксируем ту вершину многоугольника АВСDЕ, через которую F=0 выходит из ОДР. Такой вершиной является точка А(1; 2). Подставим ее координаты (1; 2) в уравнение целевой функции F и найдем .

.