14 Вопрос. Монотонность последовательности.

Последовательность { } называется возрастающей, если для всех n.: неубывающей если для всех N; убывающей, если для всех n; невозрастающей если для всех n.

Такие последовательности называются монотонными-,

Теорема Монотонная ограниченная последовательность сходится

Доказательство: Рассмотрим случай неубывающей последовательности; т.е для всех n. Так как последовательность ограничена, то существует •число А, такое что выполняется неравенство ≤А для всех n. Рассмотрим числовое множество. Х состоящее из элементов данное последовательности { }. По условию это множество ограничено сверху и не пусто. Следовательно, в силу теоремы о существовании точной верхней грани множество Х имеет точную верхнюю грань. Обозначим ее через а и докажем, что а = lim . (что а яв-ся пределом данной последовательности). Действительно, так как а -точная верхняя грань множества Х сотоящегп из элементов последовательности { }, то по свойству точной верхней грани для любого эпсило>0 найдется номер N такой, что > а - эпсило. В силу того, что последовательность { } неубывающая, то при всех n >N имеем . > а—эпсило. С другой стороны, по определению верхней, грани ≤a<a+эпсило для всех n. Таким образом, при всех п > N получаем неравенство а-эпсило< <a+эпсило, т.е. | -а|<эпсило, при всех n>N. А это по определению означает, что а- предел последовательности { }. Случай невозрастающей последовательности рассматривается аналогично. Ограниченность монотонной последовательности является необходимым и достаточным условием сходимости .

15 Вопрос. Число е.

Рассмотрим последовательность { }, Докажем, что она сходится. Для этого достаточно доказать что она возрастающая и ограниченная сверху. . I) Покажем, что 'последовательность { } возрастающая, т.е. для любого n . разложим по формуле бинома Ньютона.

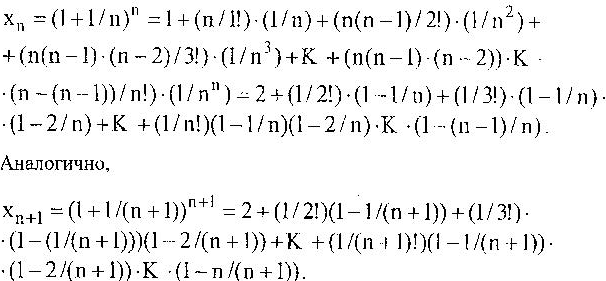
Для любого 0<к<n выпполняется соотношение (l-1/k) < (1 – 1/(k+1)).Следовательнос в выражении для каждое слагаемое больше чем в соответствующее слагаемое в выражении для . Следовательно, для любого N. Следовательно, { } - возрастающая последовательность.

2) Покажем, что последовательность { } ограниченная сверху. Рассмотрим выражение для , Так как 1 / k! <

Следовательно, для: любого n в и последовательность { } ограничена сверху, то по теореме она является сходящейся 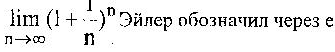Этот предел обозначается е, е=2,7182 Число е иррациональное, оно не может быть корнем никакого алгебраического.уравнения с целыми коэффициентами. Такие числа называются трансцендентными

16 Вопрос. Теорема о вложенных промежутках.

Пусть дана последовательность отрезков [a1,b1], … , [an, bn], … таких, что каждый последующий содержится в предыдущем [a1,b1]>k[an, bn]>k и пусть . Такая последовательность называется последовательностью вложенных отрезков.

Теорема Для любой последовательности вложенных отрезков существует единственная точка, принадлежащая всем этим отрезкам.

17 Вопрос. Понятие функции. Способы задания.

Пусть заданы два множества Х и У, если каждому элементу х из множества Х поставлен в соответствие по вполне определенному закону f единственный элемент у из множества У. Тогда будем говорить, что определена функциональная зависимость у от х по закону у=f(x). При этом х называют независимой переменной (или аргументом), у — зависимой переменной, Х - областью определения (или областью задания) и обозначается D (f), а множество У- областью её значений.

Элемент х из множества Х называется аргументом или независимой переменной, а элемент у из множества У- значением функции. Для того чтобы задать функцию надо задать ее область определения Х, ее область значения У, закон соответствия f, по которому определяется элемент у из множества У, соответстующий элементу х из множества Х, т.е. элемент у=F(х)

Функция область определения и множество значений которой являются подмножеством вещественных чисел называется вещественной функцией одного вещественного переменного

Функция f(x) определенная на некотором промежутке Х называется ограниченной на этом множестве сверху, если существует такое число М, что для любого х из множества Х выполняется неравенство f(x)<= M

Функция f(x) определенная на некотором промежутке Х называется ограниченной на этом множестве снизу, если существует такое число m, что для любого х из множества Х выполняется неравенство f(x) >=m.

Функция ограниченная на этом множестве сверху и снизу называется ограниченной, т.е сущ-ют числа m, M.

Классификация ф-ций:

– постоянная функция:

– степенная функция: ;

– показательная функция: ;

– логарифмическая функция: ;

– тригонометрические функции:

;

– обратные тригонометрические функции:

.

называются простейшими элементарными функциями

Если на некотором промежутке Х определена функция Z=фи(x) с множеством значений Z, а на множестве Z определена функция y=f(z), то функция y=f(фи(x)) называется сложной функцией аргумента х (или суперпозицией функций).

Пусть функция y=f(x) задана на сегменте [a,b] и пусть сегмент [α;β ] является множеством значений этой функции. Пусть кроме того каждому у из сегмента [α;β ] соответствует только одно значение Х из сегмента [a,b] для каждого y=f(x). Тогда на сегменте [α;β ] определена функция, которая каждому значению у принадлежит [α;β ] ставит в соответствие то значение хпринадлежит [a,b], для которого y=f(x). Она обозначается x=f (y) и называется обратной функции y=f(x). Замечание: Если функция x=f (y) обратная для y=f(x), то очевидно, функция y=f(x) является обратной функции x=f (y), т.е. они называются взаимообратными.

Существуют три способа задания функции: аналитический, табличный и графический. Функция задана аналитически, если закон устанавливающий соответствие между множеством всех значений аргумента и множеством всех значений функции задается посредством формул.

Аналитический способ задания фунции – основной способ задания в математическом анализе

Преимущества этого способа: сжатость, компактность задания, можно вычислить значение функции для люоого значения аргумента из области определения; имеется возможность применить к данной функции аппарат математического аналтиза

Табличный способ -заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Примеры: таблицы тригонометрических функций, таблицы квадратов, кубов, таблицы логарифмов,

При графическом способе задания функции соответствие между элементом и функцией задается посредством графика. Графиком числовой функции f. заданной на числовом промежутке X, называют множество G всех точек координатной плоскости, имеющих вид M(x,f(x)), где х принадлежит Х . то есть {(х;у): у=f(х), х принадлежит Х}

Графический способ задания функции обычно используется в практике физических измерений, в медицине, для измерения атмосферного давления - самопишущие приборы.

Преимущество этого способа—наглядность. Что делает его чрезвычайно полезным при изучении функций.