Вопрос 4. Открытые, замкнутые множества. Компактность множества. Отображение.

1)Множество х наз-ся замкнутым, если дополнение этого множества яв-ся открытым множеством. Множество называется замкнутым, если ему принадлежат все граничные точки. Пример – отрезок [a, b]

2) Множество х наз-ся открытым мн-вом, если любая точка этого множества яв-ся его внутренней точкой. открытое множество состоит из внутренних точек. Примерами открытого множества являются пустое множество, прямая, интервал (а, b).

3)Множество является компактным, если оно является замкнутым и ограниченным.

5 Вопрос. Последовательность. Действия над ними.

DEF. Если каждому числу n из натурального ряда чисел N поставлено в соответствие по определенному закону некоторое вещественное число Х, то множеств вещественных чисел называется числовой последовательностью или просто последовательностью.

Числа называются элементами или членами последовательности, x„- -общим членом последовательности, а п -его- номером

Последовательность считается заданной, если указан способ получения любого ее элемента. Задавать ее можно в виде формулы общего члена. Например, формула 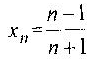задает последовательность

Для задания последовательностей используют также реккурентные соотношения. При таком способе задания обычно указывают один или несколько первых её членов и формулу, которая Позволяет найти n - ый член через предшествующие члены. Например, если , то рекуррентное соотношение при п 1 Задаёт последивателыюсть I, 2. 3,....

Не всякую последовательность можно задать формулой общего члена или рекуррентной формулой. В некоторых случаях последовательность удобно задавать алгоритмически. Примером алгоритмически заданной последовательности являются числа 0.3; 0.33; 0,333;.,., которые получаются при переводе 1 /З в десятичную Дробь, если после занятий оставлять I, 2, 3,... десятичных знаков.

Есть последовательности, которые невозможно задать выше перечисленными способами. Одной из таких последовательностей, например, являются простые числа I, 2, 3,,5, 7, 11, 13,... . В основу формирования данной последовательности положено свойство (число должно делиться только на 1 и на-себя), которым обладают-все ее. элементы.

В общем случае должен быть задан закон, по которому можно получить любой элемент последовательности.

Геометрически последовательность изображается на координатной прямой в виде последовательности точек, координаты которых равны соответствующим элементам последовательности. Над числовыми последовательностями- можно выпопнять арифметические операции. Введем эти операция, пусть даны последовательности { }.

Произведением последовательности n на число m считается последовательность mn, суммой послед- + , …, + , Разностью - , …, - , Произведением * , …, * , Частным \ , …, \ ,… если 

Вопрос 6 Ограниченные и неограниченные последовательности.

DEF. Последовательность { } называется ограниченной сверху (снизу), если существует число М ( число m) такое, что любой элемент этой последовательности удовлетворяет неравенству  <=M (х>=m), тоесть

Последовательность { } называется ограниченной, если она ограничена и сверху и снизу, т.е. существуют числа m и М такие, что любой элемент{ } этой последоватвльдасти удовлетворяет неравенству . то есть .

Пусть с = max {|m|,|M|}, тогда условие ограниченности последовательности можно записать в виде , то есть

DEF Последовательность { } называется неограниченной, если для любого положительного числа А (каким бы большим мы его ни взяли), найдётся хотя бы один элемент последовательности , удовлетворяющий неравенству