45 Вопрос. Производные функций.

см. запись на листе от руки.

будем иметь

Далее, по правилу дифференцирования сложной функции получим

46 Вопрос. Теорема о производной обратной функции.

Теорема. Если функции у = f(x) имеет в точке производную и f'( )не равно 0, то обратная функция также имеет в соответствующей точке Уо=f( ) производную, причем

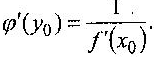
Доказательство:

Дадим аргументу у обратной функции некоторое приращение y в точке y0, y не равно0. Тогда функция получит некоторое приращение х , причем в силу возрастания (или убывания) обратной функции х не равно 0. Следовательно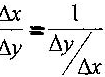

Перейдем в этом равенстве к пределу при y —> 0. Так как обратная функция непрерывна в точке у0, то и х —> 0. Но при х —> 0 предел правой части равенства существует и равен . Следовательно, существует предел и левой части, который по определению равен

Таким образом, получаем Теорема доказана.

47 Вопрос. Производные функций.

48 Вопрос. Диффеенцирование сложной функции.

Теорема. Если функция х имеет производную в точке to, а функция у= f(x) имеет производную в соответствующей точке , то сложная функция у = имеет производную в точке tо и справедлива следующая формула:

= f'(фи(to)*фи(to) (11)

Доказательство. Так как функция у = f(x) имеет производную в точке х0, то она дифференцируема в точке , то приращение этой функции в точке может быть записано в виде (12),

поделии равенство (12) на величину t не равно 0, получим 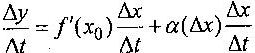(13) Равенство (13) справедливо для любых достаточно малых х .

Возьмем х равным приращению функции в точке to, соответствующему приращению t аргумента t в точке to , и устремим в этом равенстве t к нулю. Так как по условию имеет в точке to производную, то она непрерывна в этой точке. Следовательно, согласно определению непрерывности функции в точке, х —> 0 при  t ->0. имеем 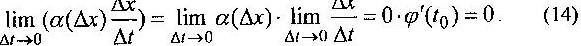В силу соотношения (14) существует предел правой части равенства (13) при t —> 0 , равный . Значит, существует предел при t—> 0 и левой части равенства (13), который по определению производной равен производной сложной функции

Таким образом, дифференцируемость сложной функции доказана и установлена формула (11).

49 вопрос. Прием логарифмического дифференцирования. Производная функции y=x в степени альфа.

Производная функции выражается формулой

Производную от степенной функции ( ) можно вычислить с помощью формулы дифференцирования сложной функции, предварительно представив функцию в виде :

50 Вопрос. Производные высших порядков.

51 Вопрос. Дифференциалы высших порядков.

Будем использовать для обозначения дифференциалов dy и dx также и символы у и х. Пусть функция f(x) дифференцируема на некотором промежутке. Тогда, ее дифференциал dy=f’(x)dx, который называется дифференциалом первого порядка или первым дифференциалом, является функцией двух переменных: аргумента х и дифференциала dх. Пусть функция f’(x) также дифференцируема на указанном промежутке. Будем полагать dx постоянным сомножителем в выражении для dy, тогда функция dy будет функцией только аргумента х и ее дифференциал в точке х выражается формулой (dy)=[f’(x)dx]=[f’(x)dx]’ х=f’’(x)dx х

Дифференциал (dx) называется дифференциалом второго порядка функции f(x) в точке х и обозначается d2y:

.