30 Вопрос. Вторая теорема Больцано-Каши.

(теорема о прохождении непрерывной функции через любое промежуточное значение),

Пусть функция f(х) непрерывна на ceгменте [a, b], причем f(a) = A, f(b) = В. Пусть С - любое число, заключенное между А и В. Тогда на сегменте [а,b] найдется точка такая, что f(хо)=С. Доказательство:

Пусть для определенности А<В и А <С<В. (Очевидно, что в доказательстве не нуждается случай А=В. В противном случае С=А=В- и можно связать =а). Рассмотрим функцию - эта функция непрерывна на [а,b] как разность непрерывных функций и принимает на концах сегмента значения разных знаков:

, Тогда по первой теореме Больцан-Коши существует точка принадлежит(а, b), в которой значение ф-ции равно 0. Получим, что . Следовательно f(Xo)=C, теорема док-на.

31 Вопрос. Точная верхняя и точная нижняя грани.

Пусть функция y=f(x) определена на множестве Х, а Y — мн-во ее значений.

Если множество Y ограничено сверху, то оно имеет точную верхнюю грань, если мн-во Y ограничено снизу, то оно имеет точную нижнюю грань.

Точная нижняя грань множества Y наз-ся точной верхней гранью функции y=f(x) на множестве X и обозначается sup f(x).

Точная нижняя грань мн-ва Y, наз-ся точной нижней гранью ф-ции y=f(x) на множестве X и обозначается inf f(x).

2 определения точной верхней и точной нижней граней ф.

Число М наз-ся точной верхней гранью ф-ции y=f(x) на мн-ве X, если выполняются условия: 1) f(x)<=M, для всех х принадлежит Х

2) для всех M ' < M, найдется х '<X, такое что f(x')>M'.

Число m наз-ся точной нижней гранью ф-ции y=f(x) на мн-ве X, если выполняются условия: 1) f(x)>=m, для всех х принадлежит Х

2)для всех m'>m, существует x' принадлежит Х: f(x)<m'.

В данных определениях, условие 1 означает, что число M (m) является одной из верхних (нижних) граней ф-ции f(x) на множестве Х. А условие 2 означает, что эта грань является наименьшим (наибольшим) и уменьшена (увеличена) быть не может.

Следствие. Если функция f{x) определена и непрерывна, на некотором промежутке X, то множество ее значений Y также представляет собой некоторый промежуток. Доказательство^ Пусть m=inff(x), M=SUpf(x). Выберем у У, так, чтобы . Выберем так, чтобы выполнялись условия . Существование таких значений ; следует из существования inff(x) и SUpf(x). Тогда по второй теореме Больцано - Коши существует точка х  Х такая, что у = f(x). Следовательно, множество Y представляет собой некоторый промежуток с концами m и М.

Если М =+со или т = -со, то .и m или M не принадлежат этому промежутку.

Лемма. Функция f(x), непрерывная в точке , ограничена в некоторой ее окрестности. Доказательство.

Пусть  = 1, тогда по определению непрерывности функции :в точке существует положительное число  такое, что для

выполняется, неравенство

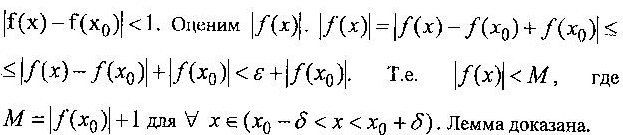
32 Вопрос. Первая теорема Вейерштрасса.

Первая теорема Вейерштрасса (теорема об ограниченности непрерывной на сегменте функции). Если функция f(x) определена и непрерывна на сегменте [а,b], то она ограничена на этом сегменте. Доказательство:

Доказательство проведем методом от противного. Пусть y = f(x) не ограничена на [a,b}. Разделим сегмент [a,b] пополам, тогда по крайней мере на одном из полученных сегментов функция не ограничена. Обозначим этот сегмент Продолжим процесс деления неограниченно, получим последовательность Это последовательность вложенных отрезков, на каждом из не ограничена (по предположению). По построению при . Тогда по теореме о вложенных отрезках существует единственная точка с принадлежащая всем этим отрезкам. Функция f{x} определена и непрерывна на [а.b]. Следовательно, она непрерывна .в точке с, но тогда по лемме существует окрестность точки с,в которой .f(x) ограничена. При достаточно большом n в эту окрестность попадает сегмент на котором функция также ограничена. Мы пришли к противоречит. Теорема доказана.

Замечание. Теорема неверна если, сегмент [a,b] заменить на интервал (a,b).