1 Вопрос. Множества. Операции над множествами.

Множество- совокупность объектов любой природы, обладающих определенным свойством. Слова «совокупность», «семейство», «система», «набор» - синонимы слова «множество».

Множество – совокупность определенных, различных между собой объектов, мыслимых как единое целое.

Примерами множеств могут служить множество предприятий некоторой отрасли, множество точек на плоскости, множество целых-чисел,

Объекты, из которых состоит множество называются его элементами или точками.

Множество может содержать конечное или бесконечное число произвольных объектов (элементов).

Множества обозначаются большими латинскими буквами, а их элементы – малыми

Если а не является элементом множества А, то будем- -писать (а не принадлежит А).

Рассмотрим два множества Х и Y. Если множества X и У состоят из одних и тех же элементов, то гово­рят, что они совпадают, и записывают Х = Y . Если все элементы множества У содержатся в множестве X,то У называется подмножеством Х и обозначается Y с Х. При этом говорят, что У включено в Х или—У содержит X. Множество не содержащее ни одного элемента, называется пустым и обозначается символом (перечеркнутый кружок). Пустое множество является подмножеством любого множества,

Множество можно задать двумя способами;

а) перечислением его элементов ( А — {2; 3; 5; 7});

б) описанием свойств элементов.

ОПЕРАЦИИ НАД МНОЖЕСТВАМИ

Рассмотрим, как по двум или нескольким данным множествам образуется новое множество. Для этого введем операции над множествами, Обозначим универсальное множество U. Пусть множества А с U и В с U . Графически операции над множествами будем изображать с помощью диаграммы Эйлера.

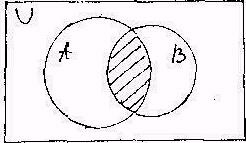
(DEF. Пересечением двух множеств А и В называется множество С; состоящее из элементов, принадлежащих как множеству А, так и множеству В, т.е. из элементов общих для множеств А и В. Пересечение С двух множеств А и В обозначается С =- А В. Множество С составляет общую часть множества А и В. Аналогично определяется пересечение произвольного конечного числа множеств А

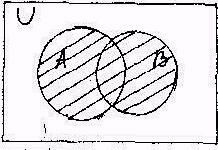
DEF. Объединением двух множеств А и В называется множество С, состоящее из элементов, принадлежащих хотя бы одному из множеств А или В. Объединение С двух множеств А и В обозначается С •= А U В: Аналогично определяется объединение произвольного конечного числа множеств А

DEF Разностью двух множеств А и В называется множество С, состоящее из элементов множества А не принадлежащих В. Разность С двух множеств А и В обозначается С = А\.В .

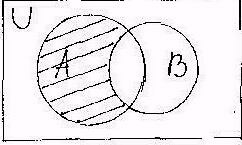
DEF Если подмножество В является подмножеством А, то разноси А\В называется дополнением В до А и обозначается В'а

DEF. Дополнением множества А называется множество, состоящее из элементов универсального множества не принадлежащих множеству А.

Дополнение до универсального множества обозначается А' или А. ...

Свойства операции над множествами:

1) коммутативность: AUB= В UА, АВ =ВА;

2) ассоциативность: (А В)  С= А (В С), (АUB)U=АU(ВU С);

3) дистрибутивность: {AUB)C=(АС)U(ВС), (А В)UC= (А UC) (ВU C);

4) (A\B) B=А BcA; -

5) принцип двойственности: (A U В)' = А’  В', (А  В)' = A' U B'.