Вопрос 19.2. Функция Лагранжа и множители Лагранжа.

Теорема 19.1. (Необходимые условия существования условного экстремума). Пусть на множестве M непрерывно дифференцируема функция и 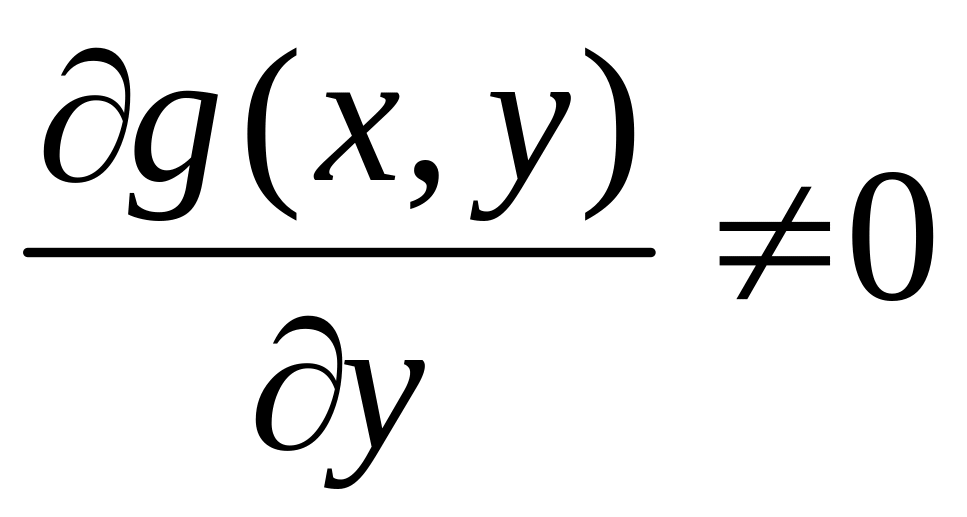. Тогда для того, чтобы точка была точкой условного экстремума функции при наличии уравнения связи необходимо, чтобы выполнялись условия

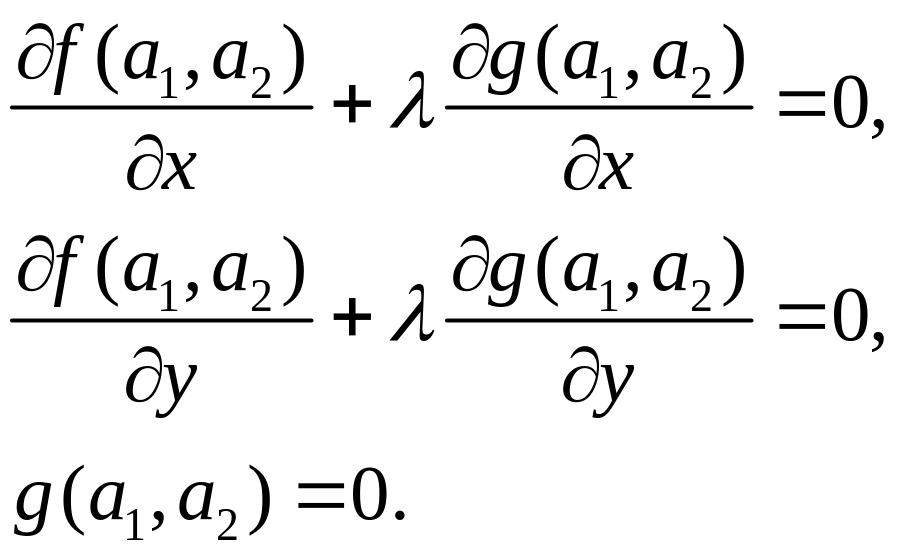
Доказательство. Из условия теоремы следует, что уравнение связи определяет неявную функцию . В точке условного локального экстремума функция имеет безусловный экстремум. Поэтому

.

Условие очевидно. Из .

Из последнего уравнения получаем . Откуда находим

.

Умножим на равенство и заменим . Тогда получим

,

или

.

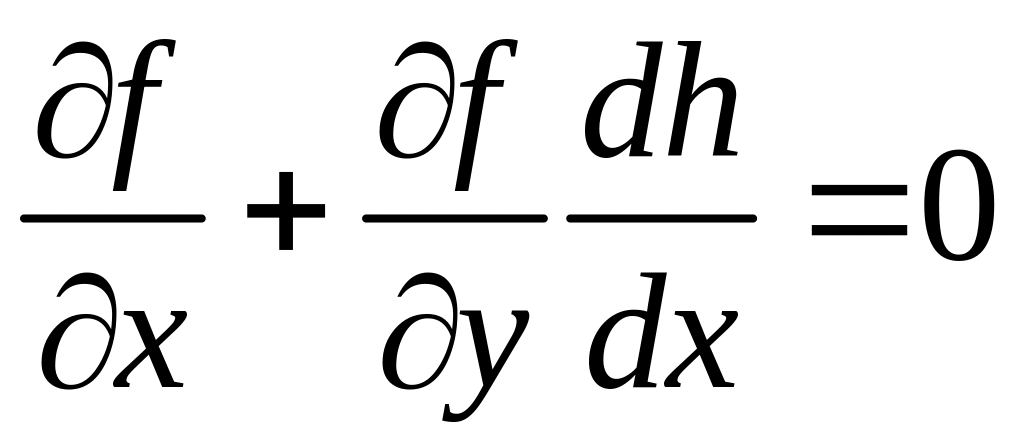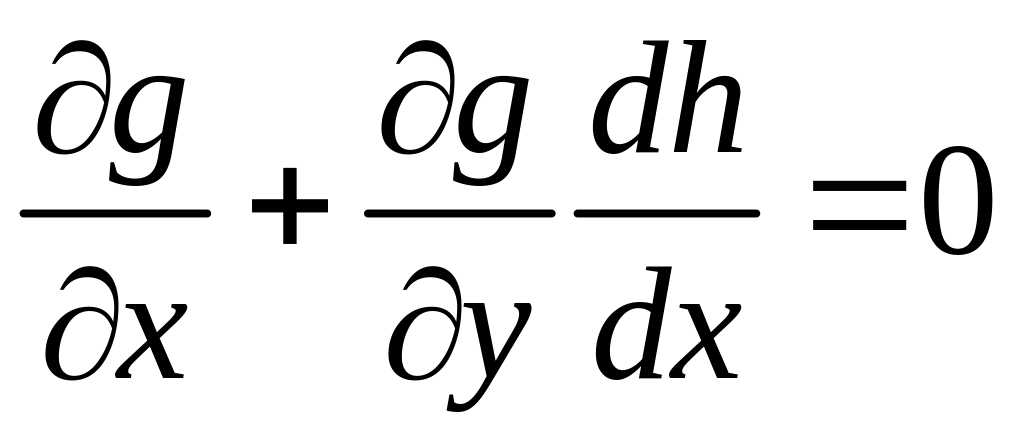Так как и , то , откуда следует доказательство теоремы.

Конец доказательства.

Замечание 19.1. Если ввести функцию Лагранжа

,

где - множитель Лагранжа, то необходимые условия существования можно свести к условиям

Если x и y удовлетворяют уравнению связи , то функция Лагранжа совпадает с функцией .

Теорема 19.2. (Достаточные условия существования условного экстремума). Пусть точка является стационарной точкой функции при наличии связи . Если второй дифференциал функции Лагранжа, вычисленный по x и y при условии что , знакопостоянен, то это точка условного локального экстремума, при чем, если , то это точка условного минимума, в противном случае - точка локального максимума. Если второй дифференциал функции Лагранжа меняет свой знак, то условного экстремума нет.

Теорема приводится без доказательства.

Пример 19.2. . Найти условный экстремум и определить тип экстремума.

Составим функцию Лагранжа . В точках локального экстремума должны выполняться условия

.

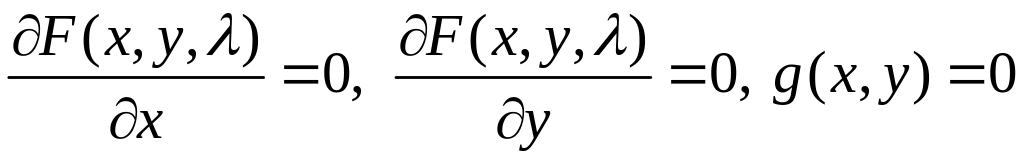откуда получаем систему уравнений

Отсюда получаем:

Вычислим второй дифференциал функции Лагранжа

С учетом уравнения связи , получим

В точке второй дифференциал отрицателен

.

Следовательно, это точка условного локального максимума. В точке второй дифференциал отрицателен

.

Следовательно, это точка условного локального минимума.

Конец примера.

Лекция № 20. Дифференциальные уравнения.

Вопрос 20.1. Задачи, приводящие к дифференциальным уравнениям.

Задача 20.1. Движение материальной точки массы m под действием силы F вдоль оси X.

На основании второго закона Ньютона запишем уравнение движения материальной точки:

,

где

m ‑ масса, a ‑ ускорение, t ‑ время, x(t) - координата, ‑ скорость.

Так как , то

.

Это обыкновенное дифференциальное уравнение второго порядка, описывающее закон движения материальной точки. Чтобы его определить однозначно, требуется задать начальные условия

Задача определения из

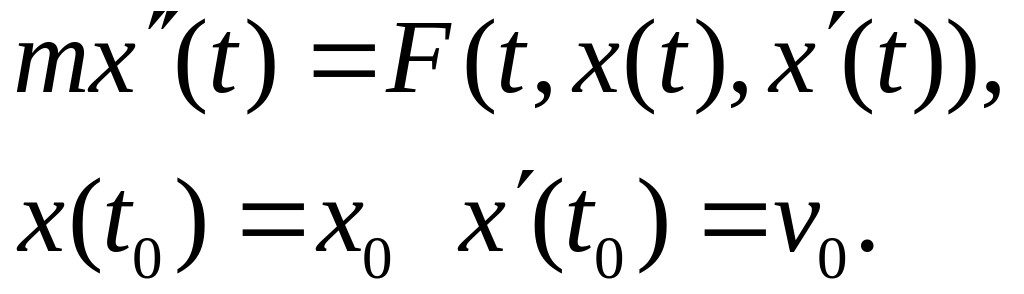
называется задачей Коши. В частности, если , то решение задачи Коши имеет вид:

.

Задача 2. Движение материальной точки массы m в пространстве под действием силы .

Уравнения движения дает второй закон Ньютона :

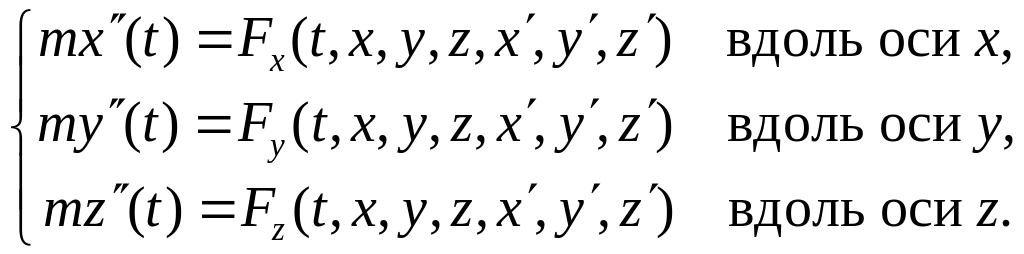
Для однозначного решения задачи зададим начальные условия:

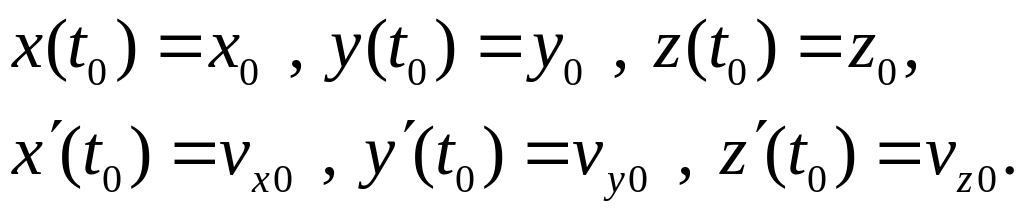
Тогда получаем уже систему обыкновенных дифференциальных уравнений второго порядка с начальными условиями. В векторной форме она выглядит так:

Задача 3. Радиоактивный распад. Химические реакции первого рода. Остывание нагретого тела. Скорость изменения численности популяции.

Пусть m(t) ‑ количество радиоактивного вещества в момент времени t. Закон радиоактивного распада утверждает, что скорость радиоактивного распада пропорциональна количеству не распавшегося вещества, то есть

.

Начальное условие .

Решение этой задачи Коши имеет вид .

Пусть m(t) ‑ количество химического вещества, которое распадается по реакции

A ® продукты реакции,

и пусть скорость распада пропорциональна количеству не прореагированного вещества, тогда уравнение реакции

.

Начальное условие . Пример реакции

.

Пятиокись азота двуокись азота

Пусть некоторое тело нагрето до температуры и оставлено остывать. Согласно закону Ньютона скорость остывания пропорциональна температуре тела, то есть

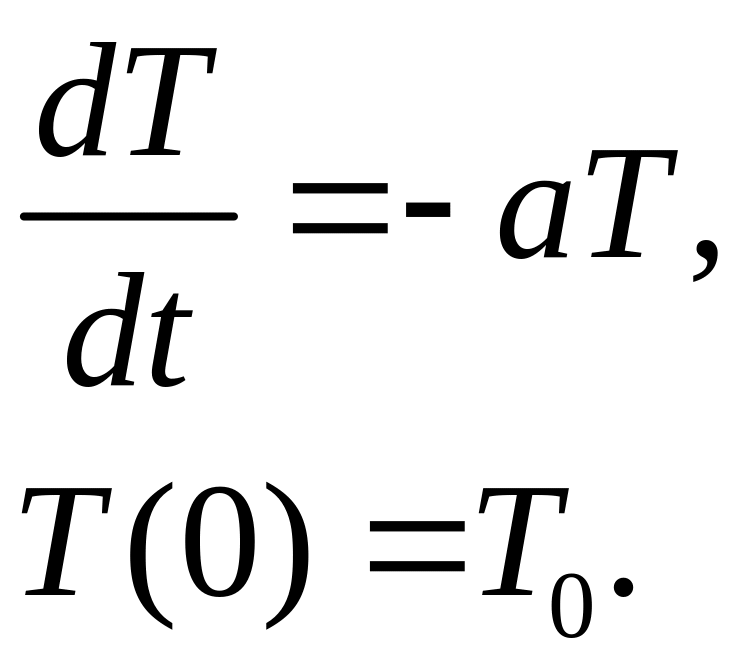
Пусть N - число особей в популяции, например, волков, тогда при больших N скорость изменения числа особей в популяции пропорциональна N:

Если , то , если , то при .

Вывод: различные физические, химические, биологические процессы описываются одним и тем же уравнением.

Задача 4. Математический маятник.

Пусть на материальную точку массы m действует упругая сила , тогда по закону Ньютона

Обозначим , тогда получим уравнение свободных колебаний

.

Задача 5. Электрические колебания в контуре.

Согласно законам Кирхгофа

,

.

Отсюда

,

или дифференцируя по t

.

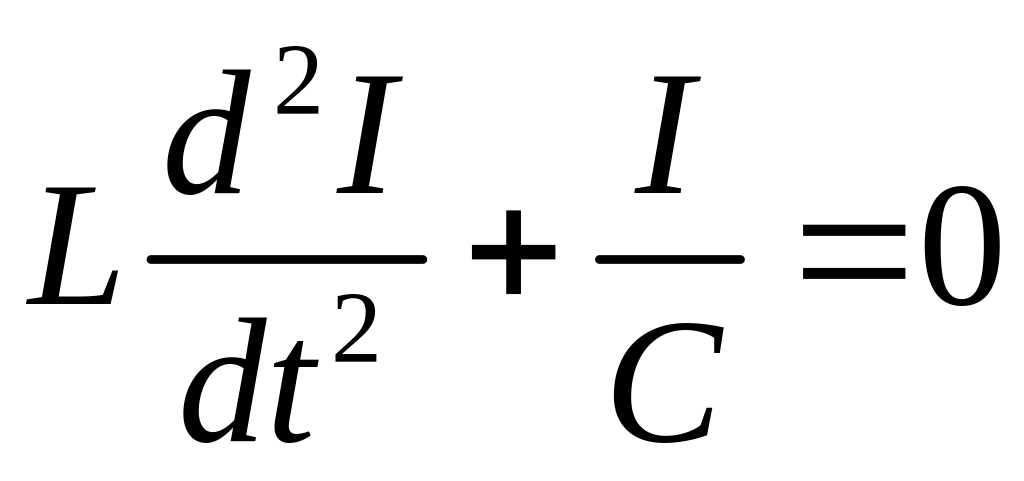Пусть , тогда после деления на L получим

.