2)Пусть существует производная. ,

,

________________________________________________

Теорема Ферма: пусть f(x) непрерывна на [a;b], пусть , если существует , тогда . Док-во: рассмотрим предел справа: рассмотрим предел слева: теорема остается верной и для inf.

________________________________________________

Теорема Роля: Эта теорема позволяет отыскать критические точки, а затем с помощью

достаточных условий исследовать ф-ю на экстремумы.

Пусть 1) ф-я f(x) определена и непрерывна на [a;b]; 2) существует производная в промежутке (a;b); 3) f(a)= f(b). Тогда между точками a и b найдется такая точка с, что производная в этой точке будет = 0. док-во. Согласно второй теореме Вейерштрасса,

1) функция const. supf(x)=inff(x)=M,

2) т.к. , а функция на концах равна, значит хотя бы 1 значение не приминается на концах отрезка. по т. Ферма

Теорема Лагранжа

Пусть 1) ф-я f(x) определена и непрерывна на интервале [a;b]

2) Существует конечная производная, по крайней мере, в открытом интервале (a;b).

Тогда между a и b найдется такая точка с, что для нее выполняется следующее

равенство: (f(b)-f(a))/(b-a)=f’(c), a < c< b

Док-во:

Введем вспомогательную ф-ю g(x).

g(x) = f(x) - f(a) - [(f(b)-f(a))/(b-a)]*(x-a)

Эта ф-я удовлетворяет всем условиям теоремы Ролля:

1) она непрерывна как разность между непрерывной и линейной функциями;

2) в открытом интервале (a;b) существует конечная производная этой ф-ии.

g’(x) = f’(x) - (f(b)-f(a))/(b-a)

3) на концах промежутка в точках a и b эта ф-я равна 0

g(a) = f(a) - f(a) - (f(b)-f(a))/(b-a)*(а - а) = 0

g(b) = f(b) - f(a) - (f(b)-f(a))/(b-a)*(b-a) = 0

g(x) непрерывна на [a;b], существует на (a;b),

f’(c) - (f(b)-f(a))/(b-a) = 0, отсюда

f’(c) = (f(b)-f(a))/(b-a)

Геометрическое истолкование

CB/AC = (f(b)-f(a))/(b-a)

На дуге АВ найдется по крайней мере одна точка М, в которой касательная ||

хорде АВ.

________________________________________________Теорема Коши: пусть f(x),g(x) непрерывны на [a;b], пусть тогда док-во: по Лагранжу

h(x) непрерывна на [a;b],

________________________________________________

Свойства о маленького:

Опр:

1) пусть дано , тогда док-во:

Пусть

2)

2)n>k, то док-во

3) док-во. Пусть

4)

________________________________________________

Форму­ла Тейлора

«О приближении гладкой ф-ци к полиномам»

Опр. Пусть ф-ция f(x) имеет в т-ке а и некоторой ее окрестности пр-ные порядка n+1. Пусть х - любое значение аргумента из указанной окрестности, ха. Тогда между т-ми а и х надутся т-ка  такая, что справедлива ф-ла Тейлора. f(x)=f(a)+f‘(a)/1!(x+a)+ f‘‘(a)/2!(x+a)^2+f^(n)(а)/n!+f^(n+1)()/(n+1)!(x-a)^(n+1).

Док-во. Сводится к Роллю путем введения вспом. переменной g(x).

g(x)=f(x)-f(a)-f‘(x)(x-a)-…-1/n!f^n(x)(x-a)^n-1/(n+1)!(x-a)^n+1. По т-ме Роляя  т-ка с из (a,b), такая что g(c)=0 =f^(n+1)(c)

________________________________________

Формула Тейлора для многочлена

Определение: (многочлена Тейлора) Пусть функция y=f(x) – n – раз дифференцируема в точке х0 многочлен (полином) вида

Tn(х)=f(x0)+[f’(x0)(x-x0)]/1!+ [f’’(x0)(x-x0)2]/2!+ [fn(x0)(x-x0)]/n! называется многочлен Тейлора с центром в точке х0 или многочленом по степеням (х-х0)

________________________________________

Разложение по формуле Тейлора произ­вольной функции

Теорема: (основное свойство многочлена Тейлора) Пусть функция y=f(x) – n – раз дифференцируема в точке х0 f(x)=Tn(x0); f’(x0)=Tn’(x0),…,f(n)(x0)=Tn(n)(x0)

Доказательство; (подстановкой) Tn(х)=f(x0)+[f’(x0)(x-x0)]/1!+ [f’’(x0)(x-x0)2]/2!+ [fn(x0)(x-x0)]/n! , подставим х0 получим Tn(x0)=f(x0). Продифференцируем многочлен Тейлора

Tn’(x)=f’(x0)/1!+[f’’(x0)2(x-x0)]/2!+ [f’’’(x0)3(x-x0)2]/3!+ [fn(x0)n(x-x0)n-1]/n!, подставим вместо х х0

Tn(x0)=f(x0)

Tn’’(x)=f’’(x0)/1!+[f’’’(x0)32(x-x0)]/3!+…+ [f(n)(x0)n(n-1)(x-x0)n-2]/n!

Tn’’(x)=f’’(x0)

________________________________________

________________________________________________

Формула Тейлора основных элементарных функций

1)

2)

Остаточный член в форме Пеано

Теорема: Пусть функция y=f(x) – n – раз дифференцируема в окрестности х0 и nая производная непрерывна в этой окрестности.

________________________________________________

Правило Лопиталя

f(x),g(x) дифференцируемы на (a,b]

Пусть

Док-во f(a)=0 g(a)=0,тогда f(x),g(x) на [a,b]

2) f(x),g(x) определены [a,+

Док-во

h(t)

h(t) дифференцируема, непрерывна (0,

z(h(t)), g(h(t)) диффрен,непрерывна (0,

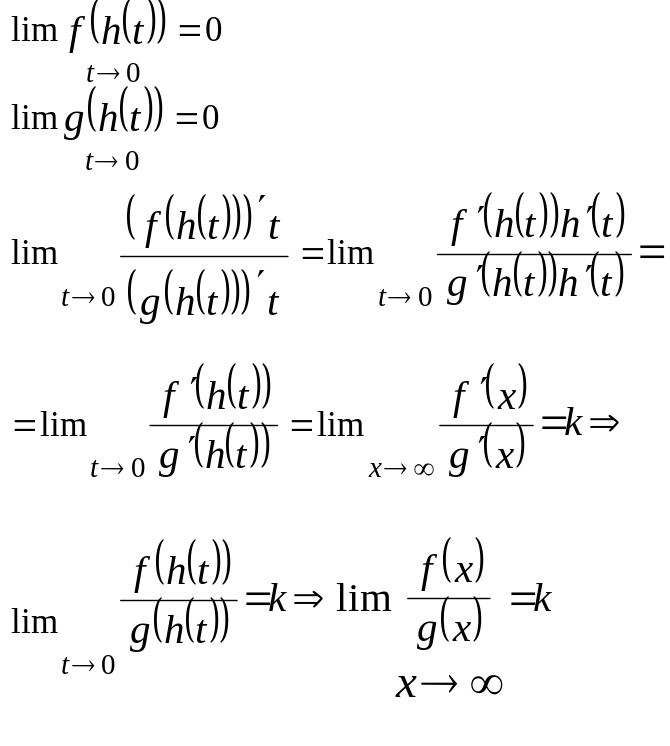
3) f(x),g(x) (a,b]

_______________________________________

Локальный экстемум

Можно указать О(х1) в которой все значения функции

f(x)<f(x1) b и О1(х1) анологично для точки х2

f(x)>f(x1) b и О2(х1). Значенгие функции в точке М1, М3 и М5 –

max; M2 и М4 – min – такие точки назавыются точкками

экстремума или точками локального max и min.

Определение: (точки экстремума)

Пусть функия f(x) определена в некоторой О(х0) и f(x)>f(x0) в

О(х0) или f(x)<f(x0) в этом случае точка х0 – называется точкой локального max (min).

Замечание:

f(x)f(x1) в О1(х1)

f(x)f(x2) в О2(х2)

говорят, что точки х1 и х2 точки не строгого локального

экстремума.

________________________________________

Необходимое условие экстемума функции в точке

Необходимое условие …

Пусть f(x) дифференцируема на (а, b)

Ǝ V(x0) x0 ∈ (a, b)

∀ x ∈ V(x0) f(x0)  ≥ f(x) ⇒ f’(x0)=0

Доказательство

По теореме Лагранжа

Пусть x ∈V(x0)

x < x0 : >0

lim =f’(слева)(x0) ≥0

x→x0-0

x>x0 : <0

lim =f’(справа)(x0) ≤0

Ǝ f’(x0)= f’(слева)(x0)= f’(справа)(x0)=0 что и требовалось доказать

________________________________________

Достаточное условие экстемума функции в точке

Достаточное условие экстремума функции в точке

Пусть f(x) принадлежит (а,b)

Существует х0 принадлежащие (a,b)

f’ (x0)=0

существует окрестность в точке х0

для любого х принадлежащего окрестности в точке х0 выполняется условие х<х0

f’(х) > 0

для любого х принадлежащего окрестности в точке х0 выполняется условие х>х0

f’(х)<0

х0 – max, т. е. для любого х принадлежащего окрестности в точке х0 выполняется условие f(x) < = f(х0)

( для любого х принадлежащего окрестности в точке х0 выполняется условие х<х0

f’(х) < 0

для любого х принадлежащего окрестности в точке х0 выполняется условие х>х0

f’(х)>0

х0 – min, т. е. для любого х принадлежащего окрестности в точке х0 выполняется условие f(x) > = f(х0) )

Доказательство

По теореме монотонности

Для любого х принадлежащего окрестности в точке х0 выполняется условие

х <х0 f(х) < f (х0)

Для любого х принадлежащего окрестности в точке х0 выполняется условие

х >х0 f(х) > f (х0)

f(х) < f (х0)

________________________________________________