1.7. Уравнение движения

Зависимость между силами, действующими в жидкости, устанав- ливается в форме уравнений движения жидкости.

Сначала установим эту связь для жидкости, движущейся без тре- ния (идеальная жидкость) и находящейся под действием сил тяжести и сил давления. Для вывода уравнения применим основной принцип ме- ханики, согласно которому тело находится в состоянии движения, если

сумма проекций всех сил, действующих на тело, равна произведению массы движущегося тела на его ускорение.

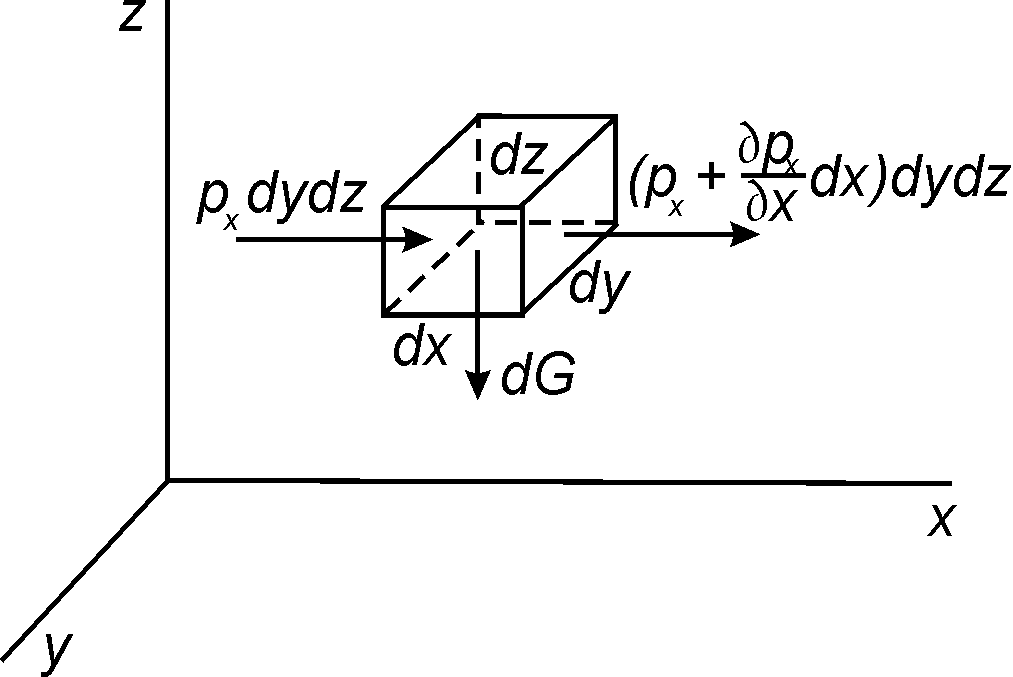
Рис. 1.5. К выводу уравнения движения

Выделим в движущейся жидкости элементарный параллелепипед с гранями dxdydz (см. рис. 1.5), выразим проекции сил, действующих на него, при этом силу тяжести dG направим по оси z. Получим для осей x, y и z соответственно

_{p dydz   p}

_{ px dx  dydz   Dwx dxdydz ,}

_{x  x x  d}

_{ }

_{p dxdz   p}

_{p  Dw}

_{ y dy dxdz   y dxdydz , (1.34)}

_{y  y y  d}

_{ }

_{dG  p dxdy   p}

_{ pz dz  dxdy   Dwz dxdydz .}

_{z  z z  d}

 

_{После сокращений и приведения к единице объема получим}

_ ^p_x

_{ } ^Dw_{x ,}

x d

_{p Dw}

_ ^y _{ } ^y _{, (1.35)}

y d

_{ } ^p_z

_{ } ^Dw_{z .}

z d

Раскрывая полные производные в правой части уравнений (1.35),

получим

_{ px}

_{   wx  w}

_{wx  w}

_{wx  w}

_{wx  ,}

_{x  }

_{x x}

_{y y}

_{z z }

_{ }

_{ py    wy  w}

_{wy  w}

_{wy  w}

_{wy  , (1.36)}

_{y  }

_{x x}

_{y y}

_{z z }

_{ }

_{  pz}

_{   wz  w}

_{wz  w}

_{wz  w}

_{wz  .}

_{z  }

_{x x}

_{y y}

_{z z }

 

Данная система дифференциальных уравнений называется диф- ференциальными уравнениями движения Эйлера.

1 . 7 . 1 . У р а в н е н и е Б е р н у л л и

Для установившегося режима движения жидкости при условии, что компоненты скорости изменяются только в направлении соответст- вующих осей, уравнения (1.36) будут иметь вид

_ ^px

^x

_p

_ ^y

y

  w_x

  w_y

^wx _,

^x

^wy _{, (1.37)}

^y

_{ } ^pz

^z

  w_z

^wz _.

^z

Уравнения (1.37) выражают действие сил в точке движущейся жидкости. Чтобы выразить действие сил по всей длине граней паралле- лепипеда (рис. 1.5), необходимо левые и правые части уравнений (1.37) умножить на длину соответствующих граней. Тогда получим

_ ^p_{x dx   w}

^w_{x dx ,}

_x ^x _x

_p

_ ^y _{dy   w}

y ^y

^wy _{dy , (1.38)}

^y

_{ dz } ^p_{z dz   w}

^w_{z dz .}

_z ^z _z

Сложив уравнения (1.38), получим полное изменение действия сил во всем объеме элементарного параллелепипеда:

_{ dz   px dx  py dy  pz dz  }

_{ x y}

_{z }

^{ } _{. (1.39)}

_{   w}

_{wx dx  w}

w_{y dy  w}

_{wz dz   0}

_{ x x}

_{y y}

_{z z }

 

Выражения, стоящие в скобках, представляют полные дифферен- циалы давления dР и квадрата скорости, так как в последнем случае любое слагаемое можно представить как

x

_{w  w}² _

_w ^x _{dx  d }

_{ . (1.40)}

^x _x

_ ² _

С учетом уравнения (1.40) выражение (1.39) можно записать в форме суммы полных дифференциалов:

_{ w}² _

_{ dz  dP   d    0 . (1.41)}

_ ² _

Интегралом уравнения (1.41) соответственно будет

_w²

_{ z  P  }

²

 const

(1.42)

или

_{P w}²

_{z    const , (1.43)}

 2 g

где z – положение рассматриваемой точки в текущей жидкости относи- тельно уровня сравнения (нивелирная высота), м; Р/ – статический на- пор в рассматриваемой точке, м; w²/2g – скоростной или динамический напор в рассматриваемой точке, м.

Уравнение (1.43) и есть уравнение движения в конечном виде, или уравнение Бернулли. Для двух рассматриваемых точек жидкости, рас- положенных на разных уровнях, уравнение Бернулли записывается в следующем виде:

_{P w}²

_{P w}²

^z₁ ^

¹ _ ¹

 2 g

^{ z}₂ ^

² _ ²

 2g

. (1.44)

Согласно уравнению Бернулли закон движения жидкости можно интерпретировать:

1) при установившемся движении идеальной жидкости для любой точки потока сумма статического и динамического напоров остается ве- личиной постоянной;

2) при установившемся движении идеальной жидкости в той точ- ке потока, где скорость больше, давление меньше;

3) при установившемся движении идеальной жидкости сумма по- тенциальной (z + P/) и кинетической энергии (w²/2g) остается величи- ной постоянной.

Хотя уравнение Бернулли получено для ограниченных условий (установившееся движение, жидкость без трения), тем не менее, оно по- зволяет решать основные задачи движения жидкостей, связывая ско- рость и давление в потоке.

1 . 7 . 2 . У р а в н е н и е Н а в ь е – С т о к с а

При учете сил трения в дифференциальное уравнение движения жидкости Эйлера необходимо ввести дополнительное слагаемое, кото-

^{рое получаем из уравнения Ньютона. Сила внутреннего трения } ₀

при

одномерном движении жидкости на единицу поверхности выражается, по Ньютону, как

_{  } ^wx _{. (1.45)}

⁰ z

Так как в уравнения (1.34) входят проекции действующих сил в движущейся жидкости на соответствующие оси координат, то для силы трения относительно оси z получим выражение

_{0  0}

_{ dxdy } ^_{ }

 ₀

_z

_

_dz ^ _{dxdy . (1.46)}

 

С учетом (1.45) и (1.46) дифференциальные уравнения неустано- вившегося движения вязкой жидкости при изменении компонентов ско- ростей по всем направлениям получим в виде

_{2 2 2}

_{ px}

_{   }

_{wx  }

_{wx  }

_{wx    Dwx ,}

_{x }

_x2

_y2

_{z 2  d}

 

_{2 2 2}

_{p  }

_ ^y _{ }

^w_{y } ^{ w}_{y } ^

^w_y ^ _{ } ^Dw_{y , (1.47)}

_{y }

_x2

_y2

_{z 2  d}

 

_{2 2 2}

_{  pz}

_{   }

_{wz  }

_{wz  }

_{wz    Dwz .}

_{z }

_x2

_y2

_{z 2  d}

 

Уравнения (1.47) называются уравнениями Навье – Стокса для не- сжимаемой жидкости.

В общем виде уравнения (1.47) не могут быть решены аналитиче- ски, так как невозможно определить граничные условия в неустановив- шемся движении вязкой жидкости. В то же время эти уравнения описы- вают ряд явлений в движущихся жидкостях и являются математической

моделью этого движения.