6.Осуществление дидактического принципа последовательности при выполнении рисунка с натуры

«Видение натуры» - это умение логически последовательно изображать ее на плоскости. Визуально тела различаются по внешним признакам, форме, размеру, прозрачности, цвету и фактуре. Все материальные предметы, создание либо человеком, либо природой, имеют общий содержательный признак – то или иное закономерное строение или конструктивные формы. Понимание конструкции формы с точки зрения ее пространственной организации, материала, из которого она создана, ее функционального назначения особенно важно для рабочего исполнителя, потому что именно эта сторона видения и понимания пластической структуры формы необходима в его профессиональной работе. Учебный рисунок имеет много вопросов и задач, которые при изображении формы в пространстве должны решаться взаимосвязано. Это композиция изображения на листе бумаги, конструкция, движение, пропорции, перспектива, светотень, цвет, фактура и т.д.

7.Построение плоскости(квадрат)в рисунке с учетом ее пространственного положения и перспективных сокращений

Выбрав желательное положение точки зрения, линии горизонта, точки Р, а также направление и величину одной из сторон квадрата (1—4), продолжим эту сторону до пересечения с линией горизонта в точке F2. Соединим затем точку F2 с точкой зрения Z и при ней построим прямой угол. Вторая сторона прямого угла, пересекаясь с линией горизонта в точке F1, определит положение второй точки схода, в которую пойдут стороны квадрата 1—2 и 4—3. Соединив крайние точки стороны 1—4 с точкой схода F1 получим направление сторон 1—2 и 4—3.

Т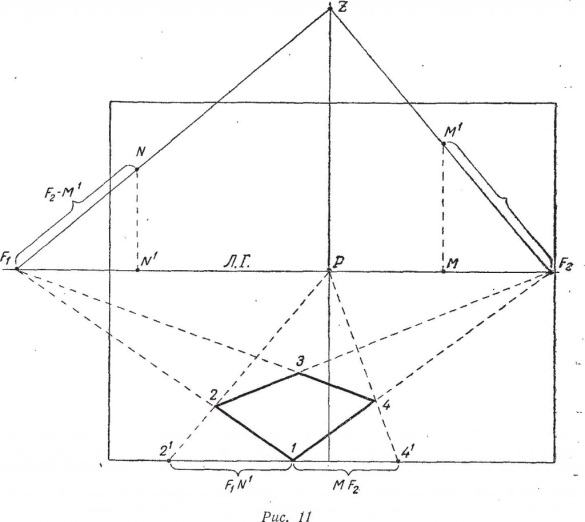 еперь остается определить истинную величину заданной стороны квадрата и отложить ее на направлении 1—F1. Из точки Р проведем прямую через точку 4 до пересечения с основанием картины в точке 41. Полученная величина 1—41 будет проекцией истинной стороны квадрата. Проекцию 1—41 отложим на линии горизонта от точки F2 в сторону к точке Р (влево) до точки М, из которой восставим перпендикуляр до пересечения в точке М1 с направлением F2 — Z.

Полученную истинную величину стороны квадрата F2M1 отложим на направлении F1 — Z до точки N. Из точки N опустим перпендикуляр до пересечения с линией горизонта в точке N1. Величина F1N1 и есть проекция стороны квадрата 1—2. От точки 1 на основании картины отложим влево полученную проекцию до точки 21. Соединим затем точку 21 с центральной точкой схода Р и на пересечении с направлением 1 — F1 получим в перспективе сторону квадрата 1—2. Соединив точку 2 с точкой F2 мы на пересечении с направлением 4—F1 получим третий угол квадрата в перспективе.

8.Построение окружности в рисунке с учетом пространственного положения и передачи перспективных сокращений

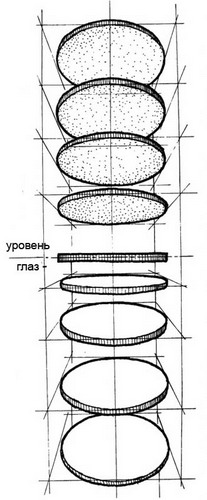
Окружность в перспективе можно построить несколькими способами, из которых остановимся на двух.

Способ 1. Для получения перспективы окружности (или любой другой кривой линии) строится перспектива достаточно большого числа её точек, которые соединяются плавной кривой линией. Перспектива каждой точки строится при помощи двух вспомогательных прямых или другим способом.

Способ 2. Около заданной окружности (или другой кривой линии) описывается квадрат (или другой многоугольник), строится перспектива квадрата или многоугольника и в него вписывается в перспективе кривая - перспектива заданной кривой.