Основные способы умножения чисел в прямых кодах на примере правильных дробей или целых чисел. Бса и математическое описание алгоритмов.
0*0=0
0*1=0
1*0=0
1*1=0
Если Х – множимое, и 
– целый положительный множитель, то
произведение 
.
Произведение S получается путём сложения частичных произведений, представляющих собой разряды множимого, сдвинутые влево в соответствии с позициями разрядов множителя. Частные произведения, полученные умножением на нуль, игнорируются. Важной особенностью операции умножения n-разрядных сомножителей является увеличение разрядности произведения до n+n=2n. Знак произведения формируется путём сложения знаковых разрядов сомножителей. Возможные переносы из знакового разряда игнорируются.
Способы:
Со старших разрядов y.
.С младших разрядов y.
C младших разрядов y.
Со старших разрядов y.
.
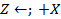Алгоритм 1. Чтобы перемножить два двоичных числа, необходимо взять модули сомножителей, сумму частичных произведений положить равной нулю, затем для каждой цифры множителя, начиная с младшей (старшей), выполнить следующее. Если 1-ая цифра множителя равна единице, то к сумме частичных произведений прибавить множимое, сдвинутое на 1 разряд влево (вправо). Знак произведения определяется сложением по модулю два кодов знаков сомножителей.
На каждом шаге алгоритмов необходимо анализировать цифры множителя. Если умножение начинается с младших чисел множителя, то на каждом шаге можно анализировать только младший (нулевой) разряд, после чего множитель сдвигается влево (делиться на 2). Если со старших разрядов, то на каждом шаге анализируется только старший цифровой разряд множителя, после чего множитель сдвигается вправо (умножается на 2).
Таблица сложения по модулю два:
Знак Х |
Знак Y |
Знак Z |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Вычисления с младших цифр множителя:
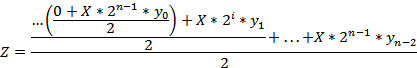
Вычисления со старших цифр множителя:
.
Алгоритм 2. Чтобы перемножить два двоичных числа, необходимо взять модули сомножителей, сумму частичных произведений положить равной 0, затем для каждой цифры множителя, начиная с младшей (старшей), выполнить следующее. Если младшая (старшая) цифра множителя равна 1, то к старшим (младшим) разрядам суммы частичных произведений прибавить множимое, в противном случае не прибавлять. Затем произвести арифметический сдвиг суммы и множителя на 1 разряд вправо (влево). Знак произведения определяется сложением по модулю 2 кодов знаков сомножителей.
Преимущества данных алгоритмов перед указанными выше состоит в том, что сумма частичных произведений и множитель сдвигаются в одинаковую сторону, при этом суммирование ведется только в старших (младших) разрядах. Все это позволяет вдвое сократить разрядность сумматора и размещать цифровые разряды множителя в младших (старших) разрядах регистра суммы, частичных произведений.
Сдвигаем множимое, и анализ разрядов множителя начинается со старших разрядов.
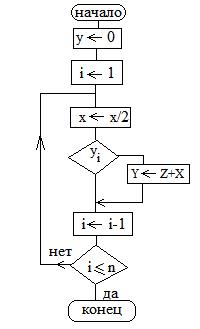
Умножение начинается с анализа младших разрядов множителя и сдвигается вправо сумма частичных произведений.
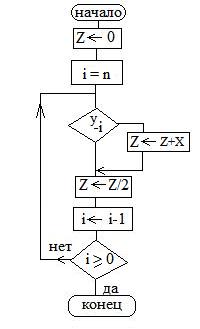
Пример:
X=11=01011; Y=19=10011.
X пр. = 0|01011; Y пр. = 0|10011