9. Представление двоичных чисел в формате с плавающей запятой: назначение разрядов числа, диапазон, погрешность представления. Математическое описание формата

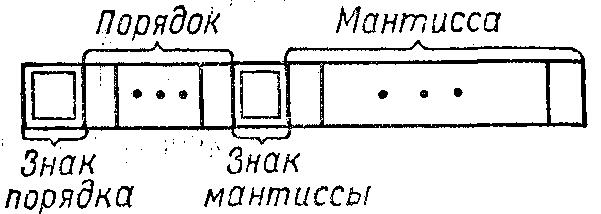
Формат с плавающей запятой позволяет избежать трудоемкого масштабирования исходных чисел и значительно увеличить диапазон и точность представляемых чисел.

Этот формат используют для хранения правильных дробей.

М – мантисса числа (правильная дробь); S – основание СС. P – порядок числа.

Мантисса и порядок задаются в системе счисления с основанием S. Знак числа совпадает со знаком мантиссы.

Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. На обычной 32-битной вычислительной машине, использующей двойную точность (64 бита), мантисса составляет 1 бит знак + 52 бита, показатель — 1 бит знак + 10 бит. Таким образом получаем диапазон точности примерно от 4,94×10⁻³²⁴ до 1.79×10³⁰⁸ (от 2⁻⁵² × 2⁻¹⁰²² до ~1 × 2¹⁰²⁴).

При фиксированном порядке абсолютная погрешность представления мантиссы постоянна в диапазоне представления М, определяется половиной веса младшего разряда мантиссы и зависит от её разрядности. Во всём диапазоне абсолютная погрешность представления зависит от порядка числа.

Устройства, реализующие операции с числами, представленными в форме с плавающей запятой, характеризует большая сложность и меньшее быстродействие.

10. Нормализованное представление числа.

Мантисса обычно представляется правильной дробью в нормализированном виде (первая цифра справа от запятой должна быть отличной от нуля). Значения нормализованных мантисс должны удовлетворять неравенству . Если это неравенство не выполняется, то такая мантисса называется ненормализованной.

Нормализованное число: x = 0.11111 * 10^-11

Ненормализованное: x = 0.0111111*10^-100

11. Формат со «скрытой» единицей.

Во многих ЭВМ старший цифровой разряд не хранится, а только подразумевается. Такая форма представления называется форматом со «скрытой» единицей.

12. Формат со смещенным порядком.

Для упрощения операций над порядками часто используют форму с плавающей запятой со смещенным порядком. Порядки – положительные целые числа, а разряд знака порядка добавляется к мантиссе.

Диапазон представлений действительных чисел в формате с плавающей запятой и смещённым порядком зависит от разрядности порядка: .

Смещенный порядок ( – это порядок, увеличенный на число (

13. Форматы чисел в i486: цс, кц, дц, от, дт, рт, д-коды.

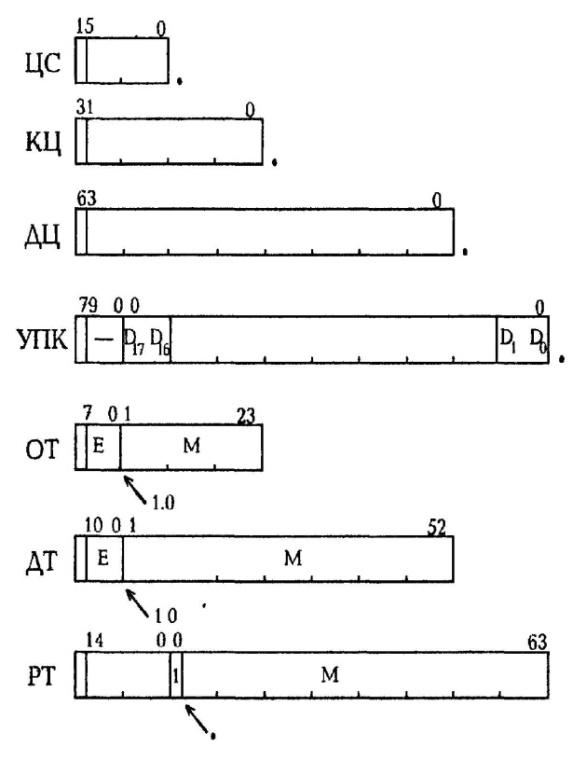
Существует 3 класса чисел:

1. Двоичные целые числа (ЦС, КЦ, ДЦ)

2. Упакованные десятичные числа (УПК)

3. Двоичные вещественные числа (ОТ, ДТ, РТ)

ЦС – целое слово.

КЦ – короткое целое.

ДЦ – длинное целое.

УПК – упакованное десятичное.

ОТ – вещественное число одинарной точности (короткое вещественное)

ДТ – вещественное число двойной точности (длинное вещественное)

РТ - вещественное число расширенной точности (временное вещественное)

Двоичные целые числа.

Три формата целых двоичных чисел (цс, кц и дц) отличаются только длиной и, следовательно, диапазоном допустимых чисел. Для представления только этих форматов используется стандартный дополнительный код. В форматы целого слова и короткого целого наибольшее положительное число кодируется как 0111…111, а наибольшее (по модулю) отрицательное число, как 1000…000.

Двоичные целые форматы существуют только в памяти. При загрузке они автоматически преобразуются в 80-битный формат РТ. Все двоичные числа точно представимы в формате РТ.

Упакованные десятичные целые числа.

УПК представляются в прямом коде и упакованном формате. Старший бит левого байта отведён для знака числа, остальные байты этого бита игнорируются, но при записи в них помещаются нули. Для десятичных чисел принят прямой код. Основная причина использования дополнительного кода заключена в том, чтобы складывать и вычитать знаковые и без знаковые целые числа одними и теми же командами. Однако в устройстве FPU нет операций над десятичными числами, а прямой код проще преобразовать в последовательность символов для печати по сравнению с дополнительным кодом. Поэтому используется прямой код.

Десятичный целые форматы существует только в памяти. При загрузке он автоматически преобразуется в 80-битный формат РТ. Все десятичные числа точно представимы в формате РТ.

Вещественные числа.

Для вещественных чисел применяют формат с плавающей запятой (ОТ, ДТ и РТ). Значащие числа находятся в поле мантиссы, поле порядка показывает положение двоичной точки в разрядах мантиссы, а бит знака S определяет разряд числа. Мантисса представлена в прямом коде.

Порядок задаётся в смещённой форме. Он равен истинному порядку, увеличенному на смещение.

E = истинный + смещение.

Смещённый порядок по-другому называется характеристикой. Её можно считать целым беззнаковым числом.

Задание порядка в форме со смещением упрощает операцию сравнения чисел в формате с плавающей точкой. Так как операции с целыми числами выполняются значительно быстрее, чем над числами с плавающей точкой, сравнение чисел с плавающей точкой осуществляется быстрее, что важно в алгоритмах с большим количеством сравнений. Например, в алгоритмах сортировки.

Числа с плавающей точкой, длинной в 32 и 64 бита, используются во многих компьютерах, и обычно называются числами с одинарной и двойной точностью. Как правило, порядок имеет фиксированную длину, определяя один и тот же диапазон представимых чисел, а для повышения точности вводятся дополнительные биты мантиссы.

При удвоении длины числа предпочтительнее часть бит отвести для расширения порядка. Поэтому порядок чисел в формате ДТ состоит из 11 бит.

В форматах ОТ и ДТ при передачах чисел и хранении их в памяти не фигурирует бит F0. Поэтому в этих форматах невозможно представить числа, которые не нормализованы. Кроме того, скрытый бит не позволяет представить в этих форматах нуль и он должен кодироваться как специальное значение.

Числа в формате РТ имеют скрытый бит F0. Такой формат позволяет немного повысить скорость выполнения операций, и обеспечить некоторые преимущества, благодаря простоте представления ненормализованных чисел.

Числа ОТ и ДТ существуют только в памяти. При загрузке они автоматически преобразуются в 80-битный РТ формат. РТ формат является единственным внутренним форматом представления чисел, причём в нём абсолютно точно кодируются загружаемые числа.