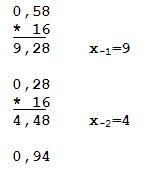1. Системы счисления. Их разновидности: непозиционные и позиционные. Их математическое описание.

Система счисления (СС) – это способ представления чисел с помощью символов, называемых цифрами. Цифры СС образуют алфавит системы счисления. Системы счисления делятся на позиционные и непозиционные.

Непозиционные СС – это системы счисления, в которых значение цифры не зависит от её позиции в записи числа. Ярким примером является Римская СС: Каждая цифра обозначает своё определенное число. Например XV: Состоит из X и V = 10+5=15. Недостаток: слишком громоздкая запись чисел, сложность вычислений.

Позиционные СС – это системы счисления, в которых значение цифры однозначно определяется позицией этой цифры в записи числа. Алфавит состоит из As={0,1,…,s}.

В соответствии с S, систему счисления называют S-ной. Если S=2, то называют двоичной.

A2={0,1}; A3={0,1,2}; A7={0,1,2,3,4,5,6}.

Числа записываются в виде последовательности цифр: X=X_nX_n-1X_n-2….X₁X₀ , X_-1X_-2…

Дробная часть от целой отделяется запятой: слева 0,1,2,…n; справа -1,-2,-3,…,-m.

Каждой позиции соответствует вес разряда. Он определяется как основание СС, возведённое в степень равную, номеру разряда.

513.79 = 5*10² + 1*10¹+3*10⁰+7*10^-1+9*10^-2 .

Длина разрядной сетки определяется, количеством разрядов, отводимых под числа.

2. Критерии выбора системы счисления при проектировании эвм.

Правильный выбор СС определяет:

1. Скорость вычисления

2. Объем памяти

3. Сложность выполнения арифметических операций.

Надо учитывать:

1. Основная СС определяет кол-во устойчивых состояний, которые должен иметь функциональный элемент, выбранный для изображения разрядов числа.

2. Длину числа

3. СС должна обеспечивать простые алгоритмы выполнения арифметических и логических операций.

Лучше всего выбирать самые экономичные системы: Экономичность системы счисления — запас чисел, который можно записать в данной системе с помощью определенного количества знаков. Чем больше запас, тем экономичнее система.

3. Перевод целых чисел из одной системы счисления в другую методом деления. Математическое описание алгоритма.

Этот способ основан на схеме Горднера:

Этот способ позволяет на каждом шаге получить одну верную цифру перевода.

Пусть исходное число представлено в СС с основанием S, нужно перевести это число в СС с основанием P и записать следующее уравнение:

которое содержит неизвестные – цифры перевода, выраженные в исходной СС. Делим обе части на основание P, и получаем:

Видно, что остаток от деления равен – младшей цифре перевода: . Целая часть частного от деления X на P имеет вид: . Алгоритм. В исходной СС делим исходное число на основание СС, в которую переводим. При этом: 1) Остаток от деления надо запомнить как цифру перевода

2) Исходное число положить равным целой части частного и повторить деление.

3) Указанные действия выполнять пока исходное число не станет равным 0.

4) Цифры записать в новой СС в обратном порядке.

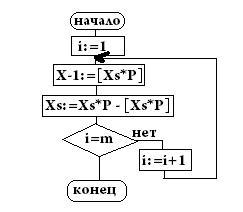
4. Перевод правильных дробей из одной системы счисления в другую методом умножения. Математическое описание алгоритма.

Перевод правильных дробей выполняется методом умножения с использованием схемы Горднера:

.

Целая часть произведения равна – старшей цифре перевода, представленной в исходной СС: . .

Алгоритм. В исходной СС умножим исходное число на основание СС, в которую переводим.

При этом: 1) Целую часть произведения запомнить как цифру перевода.

2) Исходное число положить равным дробной части произведения, после чего повторить умножение.

3) Указанные действия выполнять до тех пор, пока не будет получено необходимое количество цифр перевода.

4) Цифры записать в порядке получения.