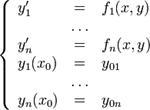Математика. Шпоры
.doc
Решением ОДУ называется функция y(x), имеющая непрерывные производные нужного порядка, исходя из уравнений, при постановке которые уравнение превращается в точку. Решением дифференциального уравнения порядка n называется функция y(x), имеющая на некотором интервале (a, b) производные y'(x),y''(x),...,y(n)(x) до порядка n включительно и удовлетворяющая этому уравнению. Частное решение диф.ур.-ф-ция превращающая ур.в подмножество. Общее решение-все множество частных результатов. Задача Коши-нахождение решения ДУ, удовлетворяющего начальным условиям.
ОДУ первого порядка, разрешённое относительно производной
Система n ОДУ первого порядка, разрешённая относительно производных (нормальная система n-го порядка)
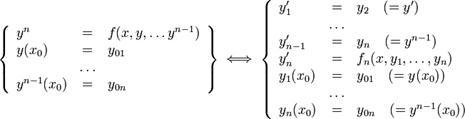
ОДУ n-го порядка, разрешённое относительно старшей производной
|
Общий вид ОДУ без выделения вектора произвольных постоянных C таков (см. п. 1.1.2):
Если (1) можно разрешить относительно старших производных, т. е. привести к виду
то путем увеличения числа неизвестных скалярных функций (см. п. 1.4.5) уравнение (2) всегда можно привести к нормальному виду
Поэтому в дальнейшем основным объектом изучения будет именно нормальная система (НС). Задача Коши, или начальная задача для уравнения (2) — это система, состоящая из (2) и начального условия
где t0 О R — начальный момент, y0 — начальное значение. Для (НС) начальное условие записывается в виде
Геометрический смысл задачи Коши (НС), (НУ) заключается в том, чтобы во множестве всех интегральных кривых системы (НС) найти ту, которая проходит через точку(t0, x0) (см. рис. 1).
График решения ОДУ y=f(x) называется интегральной кривой ДУ. Нахождение множества решений ДУ называют интегрированием ДУ |
||||||
|
2)Уравнения с разделяющимися переменными. 1. Уравнения с разделёнными переменными. Так называются уравнения вида удовлетворяющее начальному условию
Пусть
y(x)
- решение этого уравнения, т.е. f(x)dx
+ g(y(x))dy(x)
= 0. Интегрируя это тождество, получим
2. Так называются уравнения вида
Эти уравнения легко сводятся к уравнению с разделёнными переменными:
Записываем
уравнение (1)
в форме
Уравнение
(2)
делим на f2(x)
g1(y):
Эти уравнения - с разделёнными переменными. Интегрируя, получим общие интегралы:
В обоих случаях возможна потеря решений: деление на функцию может привести к уравнению, которое неэквивалентно данному. Если функция g(y) имеет действительные корни y1, y2, y3, …, то функции y = y1, y = y2, y = y3, …, очевидно, являются решениями исходного уравнения. Если функция f2(x) имеет действительные корни x1, x2, x3, …, функция g1(y) имеет действительные корни y1, y2, y3, …, то функции x = x1, x = x2, x = x3, …, y = y1, y = y2, y = y3, … являются решениями исходного уравнения. В обоих случаях эти решения могут содержаться в общем решении, но могут и не содержаться в нём; последнее может случиться, если на этих решениях нарушаются условия теоремы существования и единственности решения задачи Коши.
|
7)ОДУ высших порядков. Простейшие случаи, допускающие понижение порядка уравнения..
Дифференциальным
уравнением порядка n
называется уравнение вида:
В
некоторых случаях это уравнение можно
разрешить относительно y(n):
Так же как и уравнение первого порядка, уравнения высших порядков имеют бесконечное количество решений. Опр. Решение y=φ(x) удовлетворяет начальным условиям x0, y0, y0’, …, y0(n-1), если φ(x0)=y0, φ’(x0)=y0’, …, φ(n-1)(x0)=y0(n-1). Уравнения, допускающие понижение порядка. Понижение порядка диф ур-ния – основной метод решения ур-ний высших порядков. Этот метод дает возможность сравнительно легко находить решение, однако, он применим далеко не ко всем ур-ниям. Рассмотрим случаи, когда возможно понижение порядка. Уравнения вида y(n) = f(x). Если f(x) – ф-ция непрерывная на некотором промежутке a<x<b, то решение может быть найдено последовательным интегрированием.
|
||||||
|
3.Линейное
однородное уравнение первого порядка
Общее
решение:
Линейное неоднородное уравнение первого порядка
Общее решение:
Метод Лагранжа (метод вариации произвольных постоянных) Постановка
задачи. Найти
решение задачи Коши для линейного
неоднородного уравнения с постоянными
коэффициентами с начальными условиями
План решения. 1. Записываем соответствующее однородное уравнение с постоянными коэффициентами
Находим
фундаментальную систему решений
2. Применяем метод Лагранжа (метод вариации произвольных постоянных). Если
известна фундаментальная система
решений
где
функции
|
Интегрируя,
находим функции
3. Используя начальные условия (2), находим решение задачи Коши Метод Бернулли.
Дифференциальное
уравнение Бернулли имеет вид
|
||||||
|
4.Структура решения линейного неоднородного ОДУ. Теорема (о структуре общего решения неоднородного дифференциального уравнения). Общее решение неоднородного дифференциального уравнения есть сумма какого-либо его частного решения и общего решения соответствующего ему однородного уравнения:
где
y(n) + a1 y(n-1) + ... +an y = 0, Докажем теорему для уравнения второго порядка y// +py/ + qy = f (x). (4) где
p, q –
константы,
f
(x)
Рассмотрим соответствующее однородное ДУ: y// +py/ + q = 0. (5) Обозначим y1, y2 его линейно независимые частные решения и y0 = c1y1 + c2y2 – его общее решение.) Пусть
Перегруппируем:
Получаем
тождественное равенство, так как
первая скобка обращается в нуль в силу
того, что y0–
общее решение однородного ДУ(5), а
вторая скобка равна правой части, так
как
Принцип суперпозиции Если yk(x) - решение линейного уравнения
то
|
5
Если α — действительное число, отличающееся от 0 и 1, т.к. при α=0 и α=1 ур-ние обращается в линейное. Данное ур-ние решается 2 способами:
1.Из
него можно сделать линейное ур-ние,
разделив
2..Решать точно так же как и однородное ур-ние, поскольку левая часть у них одинаковая.
|
||||||
|
6.Рассмотрим уравнение вида F ( x , y , y ' ) = 0 , не разрешённое относительно производной. Если попытаться выразить из него y ' , то можно получить , вообще говоря , несколько уравнений
Геометрически
это означает , что в каждой
точке Различные постановки задачи Коши ОДУ первого порядка, разрешённое относительно производной
Случай 1. Уравнение вида x=f(y,y').
В
этом случае переменная x
выражается явно через переменную y
и ее производную y'.
Введем параметр
|
Поскольку
Получаем явное дифференциальное уравнение, общее решение которого описывается функцией
где C − произвольная постоянная. Таким образом, общее решение исходного дифференциального уравнения определяется в параметрической форме системой двух алгебраических уравнений:
Если из этой системы исключить параметр p, то общее решение можно выразить в явном виде x = f(y,C) Уравнение Лагранжа Дифференциальное уравнение вида
где φ(y') и ψ(y') − известные функции, дифференцируемые на некотором интервале, называется уравнением Лагранжа. Уравнение Клеро Уравнение Клеро имеет вид:
где ψ(y') − некоторая нелинейная дифференцируемая функция. Уравнение Клеро является частным случаем уравнения Лагранжа, когда φ(y') = y' Огибающая семейства кривых Пусть
дано семейство гладких кривых
|
||||||
|
8 вопрос Линейное ОДУ n-гопорядка Линейным дифференциальным уравнением n –го порядка называется уравнение вида
y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x).
Коэффициенты уравнения an-1(x), an-2(x), ..., a1(x), a0(x) и правую часть f(x) полагаем непрерывными на отрезке [a;b] .
y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x) — неоднородное линейное дифференциальное уравнение n–го порядка,
y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0 — однородное линейное дифференциальное уравнение n–го порядка,
Выражение в левой части уравнения называется линейным дифференциальным оператором n –го порядка:
L(y) ≡ y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y.
L(y) = 0 и L(y) = f(x) — соответственно однородное и неоднородное уравнения в операторной записи. При изучении линейных дифференциальных уравнений используются пространства C[a;b] — пространство непрерывных на отрезке [a;b] функций, и Ck [a;b] — пространство функций, непрерывных на [a;b] , вместе со своими производными до k –го порядка включительно. Задача коши
Линейным дифференциальным уравнением n –го порядка называется уравнение
y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x),
в которое неизвестная функция y = y(x) и все ее производные входят линейно.
Справедлива следующая теорема существования и единственности решения задачи Коши для линейного уравнения.
Если в уравнении y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x) все коэффициенты ai(x) и правая часть f(x) непрерывны на отрезке [a;b] , то задача Коши для этого уравнения с начальными условиями
y(a) = y0, y '(a) = y1,0 , ..., y(n − 1) (a) = yn,0 имеет единственное на всем отрезке [a;b] решение y = y(x) .
Следует понимать, что теорема имеет "глобальный" характер — решение существует и единственно всюду, где непрерывны коэффициенты и правая часть уравнения.
Линейная зависимость и независимость
Справедливо следующее утверждение.
Функции y1(x), y2(x), ..., yn(x) линейно зависимы на отрезке [a;b] тогда и только тогда, когда хотя бы одна из них является на этом отрезке линейной комбинацией других . Очевидны следующие утверждения.
• Если среди функций y1(x), y2(x), ..., yn(x) есть нулевая функция, то функции линейно зависимы.
• Если функции y1(x), y2(x), ..., yk(x) линейно зависимы, то при любых yk + 1(x), yk + 2(x), ..., yn (x) функции y1(x), y2(x), ..., yk(x), yk + 1(x), ..., yn(x) также линейно зависимы.
• Если функции y1(x), y2(x), ..., yn(x) линейно зависимы на отрезке [a;b] , то они линейно зависимы и на любом отрезке, лежащем внутри [a;b] .
• Если функции y1(x), y2(x), ..., yn(x) линейно независимы на [a;b] , то они линейно независимы и на любом отрезке, содержащем отрезок [а;b] (если, они определены на этом отрезке).
Вектор–функции
Y1(x), Y2(x), ..., Yn(x),
|
называются линейно зависимыми на отрезке [a;b] , если существуют постоянные α1, α2, ..., αn , не равные нулю одновременно и такие, что
α1 Y1(x) + α2 Y2(x) + ... + αn Yn(x) = 0
для всех x из отрезка [a; b].
В противном случае функции Y1(x), Y2(x), ..., Yn(x) называются линейно независимыми.
Критерий линейной независимости
Критерий линейной независимости функций. Если (n - 1) раз дифференцируемые функции F1,F2…Fn линейно зависимы на сегменте [a,b],W(x)=0 на [a,b].
Если
линейно независимые функции F1,F2…Fn
являются решениями линейного
однородного уравнения
Где Pj(j=1,n) непрерывные на сегменте [a,b] функции, то W(x)не равен 0 на [a,b].
Общее
решение рассматриваемого уравнения
при
Линейные дифферинциальный оператор n-го порядка
Понятие о линейном дифференциальном операторе n-го порядка
Для упрощения дальнейшего изложения обозначим левую часть линейного уравнения (10.1) через L(y):
L(y) ≡ y (n) + p1 (x) y (n – 1) + … + pn – 1 (x) y ' + pn (x) y. (10.3)
Таким образом, L(y) есть результат выполнения над функцией y операций, указанных в правой части формулы (10.3), а именно: вычисление производных от функции y вплоть до порядка т включительно, умножение y0, , …, , на заданные функции p1, …, pn, 1 и сложение полученных произведений. Совокупность этих операций обозначим символом L: L ≡ + p1 (x) + pn – 1 (x) + pn (x) и будем называть его линейным дифференциальным оператором n-го порядка. В частности, линейный дифференциальный оператор второго порядка имеет вид L ≡ + p1 (x) + p2 (x). Линейный дифференциальный оператор L обладает следующими основными свойствами (линейность оператора L): 1) постоянный множитель можно выносить за знак оператора
L(ky)=kL(y); 2) оператор от суммы двух функций равен сумме операторов от этих функций
L(y1 + y2) = L(y1) + L(y2).
Из этих основных свойств оператора L следует, что L Ck yk = Ck L(yk).
т. е. оператор от линейной комбинации m функций равен линейной комбинации операторов от этих функций. Используя оператор L, можно записать неоднородное и однородное линейные уравнения (10.1) и (10.2) соответственно в виде L(y) = f (x) и L(y) = 0 Матрица Грама Если функция y = y(x) является решением уравнения L(y) = f (x) или L(y) = 0. в некотором интервале (a, b), то значение оператора L от этой функции равно f (x) или нулю при всех x из (a, b): L(y(x)) ≡ f (x) (a < x < b) или L(y(x)) ≡ 0 (a < x < b).
|
||||||
|
9.Определитель Вронского системы функций. Свойства определителя Вронского системы функций и системы решений линейного ОДУ n-ого порядка.
Вронскиа́н (определитель Вронского)
системы функций
Также
вронскианом называют функцию, заданную
определителем более общего вида. А
именно, пусть задано n вектор-функций
Определитель Вронского применяется для решения дифференциальных уравнений, например для того, чтобы узнать, являются ли найденные решения однородного линейного дифференциального уравнения (либо системы уравнений) линейно независимыми. Это помогает в поиске его общего решения. СВОЙСТВА:
|
Справедливо следующее необходимое условие линейной зависимости функций. 1)Если функции f1(x), f2(x), ..., fn(x) линейно зависимы на отрезке [a;b], то их определитель Вронского тождественно равен нулю на этом отрезке:W(x; f1(x), f2(x), ..., fn(x)) ≡ 0 на [a;b]. 2) обратное утверждение неверно. Определитель Вронского линейно независимой системы функций может быть тождественно равен нулю. 3)но если определитель Вронского системы функций на некотором отрезке отличен от тождественного нуля, то система функций линейно независима на этом отрезке. ПРИМЕР: Убедимся, что вронскиан линейно-зависимых функций 1,x2,3 + 2x2 равен нулю:
Проверим теперь линейную независимость функций 1,x,x3
Есть точки, где вронскиан отличен от нуля (в нашем случае это любая точка, кроме x=0). Поэтому на любом промежутке эти функции будут линейно независимыми.
|
||||||
|
|
|



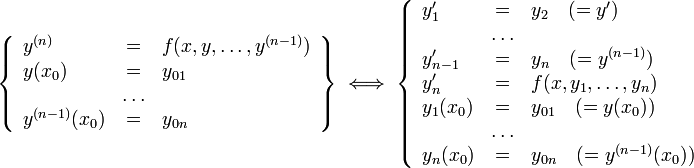

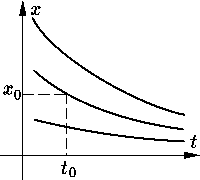

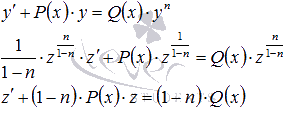 .
После
решения этого уравнения и проведения
обратной замены получаем искомое
решение.
.
После
решения этого уравнения и проведения
обратной замены получаем искомое
решение. )Уравнение
Бернулли, два метода его решения
)Уравнение
Бернулли, два метода его решения