
МАТАН (шпоры)
.doc|
8.Линейная зависимость и линейная независимость векторов. Векторы назыв.коллинеарными,если лежат на | | прямых или на одной прямой. Векторы назыв.компланарными,если они лежат на | | плоскостях или на одной плоскости. Нулевой
вектор считается коллинеарным любому
другому вектору. Нулевой вектор
считается компланарным любой паре
векторов. Векторы
из
которых хотя бы один отличен от нуля,
т.е. В |
Система
векторов называется линейно
независимой,если равенство
Критерий.
Для линейной
зависимости векторов
Св-ва: 1.Если среди векторов имеется нулевой вектор,то эти векторы линейно независимы. 2.Если часть векторов являются линейно зависимыми,то все эти векторы-линейно зависимые. 1.Один вектор линейно независим тогда и только тогда, когда он ненулевой. 2.Два вектора линейно независимы тогда и только тогда, когда они неколлинеарны.3.Три вектора линейно независимы тогда и только тогда, когда они некомпланарны.
|
|
||||
|
9.Определение базиса и размерности линейн.пространства. Базисом в пространстве называется любая упорядоченная тройка линейно независимых векторов. n-мерным пространством назыв.упорядоченная совокупность n действительных чисел,записываемых в виде X=(X1,X2...Xn),где Xi-i-я компонента вектора X. 1.x+y=y+x-коммутативное св-во суммы 2.(x+y)+z=x+(y+z)-ассоциативное(сочетательное) 3. ассоциативное относительно числового множителя св-во 4. дистрибутивное(распределит.) относительно суммы векторов св-во 5. дистрибутивное относит.суммы |
числовых множителей св-во 6.Существует нулевой вектор 0=(0,0,…0) такой, что х+0=х для любого вектора х 7. Для любого вектора х существует противопол. Вектор(-х) такой,что х+(-х)=0 8.1*х=х для любого вектора х(особая роль числового множителя 1). Множество векторов с действительн.компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее 8 св-ам,назыв.векторным пространством. Линейное пространство R назыв.n-мерным,если в нём существует n линейно независимых векторов, а любые из (n+1)векторов уже явл.зависимыми.
|
|
||||
|
9.Определение базиса и размерности линейн.пространства. Размерность пространства-это максим.число содержащихся в нём линейно независимых векторов. Число n назыв.размерностью пространства R и обозначается dim(R). Совокупность n линейно независимых векторов n-мерного пространства R назыв.базисом.Скалярным произведением двух векторов X=(X1,X2,...Xn) и Y=(Y1,Y2,...Yn)называется число (X,Y)=X1Y1+X2Y2+...+XnYn= Св-ва скалярного произведения: 1.(x,y)=(y,x)-коммутативное св-во 2.(x,y+z)=(y,x)+(x,z)- дистрибутивное 3. 4.(x,x)>0,если х-ненулев.вектор;(х,х)=0,если х-нулевой вектор. |
Линейное(векторное)пространство,в котором задано скалярное произведение векторов, удовлетв.4ем св-ам,назыв.евклидовым пространством.Длиной(нормой)вектора х в евклид.пространстве назыв.корень квадратный из его скалярного квадрата:|x|=… Св-ва:1.|x|=0 тогда и т.т.,к. х=0 2. 3.|(x,y)| |x||y| 4.|x+y| |x|+|y| (неравенство тр-ка). Два вектора называются ортогональным,если их скалярное произведение равно нулю. Векторы l1,l2,...ln n-мерного евклид.пространства Образуют ортонормированный базис,если эти векторы попарно ортоганальны и норма каждого из них равна единицы,т.е.если (li,lj)=0 при i j и |li|=1 при i=1,2,...n. |
|
||||
|
9.Определение базиса
и размерности линейн.пространства.
Пусть дан базис
|
Построим
новые векторы
|
|
||||
|
9.Определение базиса и размерности линейн.пространства. Числа
1.
|
В
О
|
|
||||
|
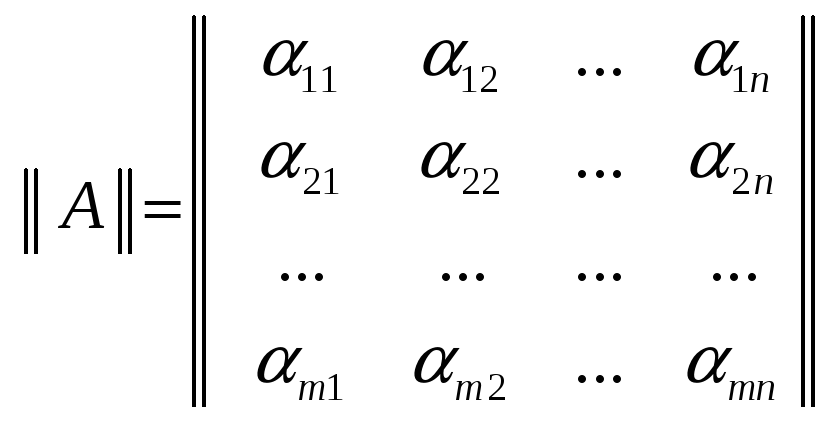
10.Определение базисного минора матрицы. Лемма.Ранг.Вычисление ранга. Матрицей размера mxn называется упорядоченная прямоугольная таблица (или массив) чисел, содержащая m строк и n столбцов. Минором Mij элемента aij матрицы n-го порядка назыв.определитель матрицы (n-1)-го порядка, полученной из матрицы А вычеркиванием i-й строки и j-го столбца.Базисным минором матрицы называется любой её ненулевой минор максим. порядка.Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю.Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы. |
Теорема о базисном миноре.В произвольной матрице А каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор. Таким образом, ранг произвольной матрицы А равен максимальному числу линейно независимых строк (столбцов) в матрице.Если А- квадратная матрица и detA = 0, то по крайней мере один из столбцов – линейная комбинация остальных столбцов. То же самое справедливо и для строк. Данное утверждение следует из свойства линейной зависимости при определителе равном нулю. Если
Рангом матрицы А назыв.наивысший порядок отличных от нуля миноров этой матрицы. Ранг матрицы А обознач.rang A или r(A).1)ранг матрицы Аm*n не превосходит меньшего из её размеров, т.е. r(A) min(m,n).2)r(A)=0тогда,кога все элементы матрицы равны нулю,т.е. A=0. 3)для квадратной |
|
||||
|
10.Определение базисного минора матрицы. Лемма.Ранг.Вычисление ранга. матрицы n-го порядка r(A)=n тогда и т.т.к. матрица А-невырожденная.Невырожденная матрица ― квадратная матрица, определитель которой отличен от нуля Элементарные преобразование матрицы: 1.Отбрасывание нулевой строки(столбца) 2.Умножение всех элементов строки(столбца) матрицы на число,не равное нулю. 3.Изменение порядка строк(столбцов) матрицы 4.Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки(столбца),умноженных на любое число. 5.Транспонирование матрицы. Ранг матрицы не изменяется при элементарных преобразованиях матрицы. |
Рангматрицы-кол-во ненулевых строк ступенчатой матрицы,которые получаются из исходной с помощью элементарных преобразований.
|
|
||||
|
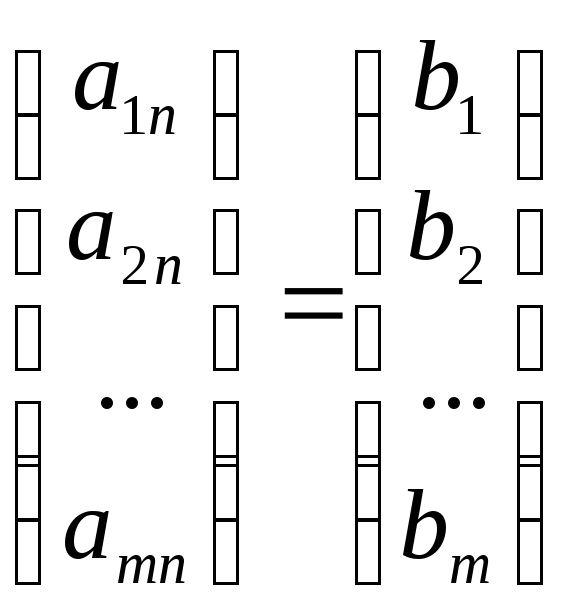
11. Системы линейных алгебраических уравнений (СЛАУ).Координатная и матричная формы записи.Равносильность СЛАУ. Система m уравнений с n неизвестными в общем виде записывается следующим образом:
где aij – коэффициенты, а bi – постоянные. Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.
|
Система
называется определенной,
если она имеет только одно решение и
неопределенной,
если более одного. Матрица
|
|
||||
|
11. Системы линейных алгебраических уравнений (СЛАУ).Координатная и матричная формы записи.Равносильность СЛАУ. Однородная система
уравнений всегда является совместной. Для этой системы набор чисел Х1=0,Х2=0…Хn=0 является решением. Рассмотрим неоднородную систему m линейных алгебраических уравнений относительно n неизвестных x1 , x2 , ..., xn: В отличие от однородной системы, эта система совместна не всегда. Справедливо утверждение (теорема Кронекера-Капелли). |
Для того, чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы. Исследовать неоднородную систему — это значит установить, является ли она совместной, и если является — найти выражение для общего решения системы. Две системы равносильны (или эквивалентны), если у них одно и то же множество решений: любое решение первой системы является решением второй и любое решение второй является решением первой. |
|
||||
|
12.Теорема Кринекера-Капелли о совместности СЛАУ.Решение СЛАУ с помощью обратной матрицы.Крамер.Гаусс.Критерий определен.слау Теорема Кронекера-Капелли: Система линейных уравнений совместна тогда и только тогда.когда ранг матрицы системы равен рангу расширенной матрицы этой системы. RgA = RgA*. Очевидно, что система (1) может быть записана в виде:
x1
|
Доказательство. 1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход АА* не изменяют ранга. 2) Если RgA = RgA*, то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.базисн.минор(билет10). Для совместных систем линейных ур-ий равны следующие теоремы:1.Если ранг матрицы совместн.системы равен числу переменных,т.е. r=n, то система имеет единственное решение. 2.Если ранг матрицы совместной системы меньше числа переменных,т.е. r<n,то система
|
|
||||
|
12.Теорема Кронекера-Капелли о совместности СЛАУ.Решение СЛАУ с помощью обратной матрицы.Крамер.Гаусс.Критерий определен.слау н R<m ур-ия r(A)=r(A1) r<n Сис-ма Системы Сис-ма неопредел. Система m Л Уравнений с n Пременными R=m ур-ия r(A)=r(A1)=r r=n Сис-ма независим. Совместная ( 1 решение)
|
Решение СЛАУ с помощью обратной матрицы. Д Т Метод Гаусса.-метод последовательных исключений переменных-с помощью элементарных преобразований система ур-ий приводится к равносильной системе. Ступенчатого(ии тр-го вида) После отбрасывания «лишних»ур-ий возможны два случая:а)число ур-ий системы равно числу переменных т.е.r=n(тр-ый вид)б)r<n(ступенчат.вид) |
|
||||
|
13.Решение
однородных СЛАУ.Критерий существования
ненулевого решения. Фундаментальная
система. Система
m
линейных ур-ий с n
переменными назыв.системой линейных
однородных ур-ий,если все их свободные
члены равны нулю.Имеет вид:
Всегда является совместной.Решение однородн.СЛАУ обладают следующ.св-ами: 1.Если строка l1=(k1,k2,...kn)-решение системы,то и строка …. -также решение этой системы.2.Если строка l1=(k1,k2,...kn) и l2=(l1,l2,...ln)-решения системы,то при любых c1 и c2 их линейная комб-ия c1,l1+c2,l2=(c1k1+c2l1,c1k2+c2l2+...c1kn+c2ln) также решение данной системы. |
Критерийненулевого решения однор.СЛАУ: Система линейных однородных уравнений имеет ненулевые решения тогда и только тогда,когда ранг её матрицы коэффициентов при переменных меньше числа переменных,т.е. при r(A)<n Система линейно независимых решений l1,l2,...lk назыв.фундаментальной,если каждое решение системы является линейной комбинацией решений l1,l2,...lk. Если ранг r матрицы коэффициентов при переменных системы линейных однородных ур-ий меньше числа переменных n,то всякая фундаментальная система решений системы состоит из n-r решений. Поэтому общее решение системы линейных однородных ур-ий имет вид: c1,l1+c2,l2…+сklk,где l1,l2,...lk-любая фундаментальная система решений, с1,с2…сk-произвольные числа и k=n-r. |
|
||||
|
14.Декартова прямоуг.система координат.Линейные операции над векторами.Вычисление длины вектора. Декартовой системой координат в пространстве называется совокупность точки и базиса. Точка называется началом координат. Прямые, проходящие через начало координат называются осями координат. 1-я OX – ось абсцисс 2-я OY – ось ординат 3-я OZ – ось аппликат. Базис-множество векторов в линейном пространстве, таких, что любой вектор пространства может быть представлен в виде некоторой их конечной линейной комбинации (полнота базиса), при этом ни один из базисных векторов не представим в виде конечной линейной комбинации остальных (линейная независимость). Базис называется ортонормированным, если его векторы попарно ортогональны и равны единице. Декартова система координат, базис которой ортонормирован называется декартовой прямоугольной системой координат. 1.Проекция суммы векторов на какую-нибудь ось равна сумме их проекции на эту же ось… |
2.При умножении вектора на число проекция умножается на это же число… Векторы назыв.коллинеарными,если лежат на | | прямых или на одной прямой.Признаком коллинеарности 2-х векторов является пропорциональность их координат. Х1 =Y1 =Z1 Х Чтобы найти компоненты вектора нужно из координат его конца вычесть координаты начала. Если
заданы точки А(x1,
y1,
z1),
B(x2,
y2,
z2),
то
|
|
||||
|
14.Декартова прямоуг.система координат.Линейные операции над векторами.Вычисление длины вектора. Если точка М(х, у, z) делит отрезок АВ в соотношении /, то координаты этой точки определяются как:
В частном случае координаты середины отрезка находятся как: x = (x1 + x2)/2; y = (y1 + y2)/2; z = (z1 + z2)/2. Приложение.Пример.
Даны векторы
|
Тогда
Итого,
координаты вектора
|
|
||||
|
22.Кривые второго порядка на плоскости:эллипс, гипербола,парабола. Определения,вывод их канонических ур-ий.Фокусы,эксцентриситет,директр. Кривая второго порядка может быть задана уравнением Ах2 + 2Вху + Су2 + 2Dx + 2Ey + F = 0. Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.
a2x2 – c2y2 = 0 – уравнение двух пересекающихся прямых. y2 = 2px – уравнение параболы. y2 – a2 = 0 – уравнение двух параллельных прямых |
y2 + a2 = 0 – уравнение двух “мнимых” параллельных прямых. y2 = 0 – пара совпадающих прямых. (x – a)2 + (y – b)2 = R2 – уравнение окружности. Эллипсом назыв.геометрическое место точек,для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина,большая,чем рассточние между фокусами. Гиперболой назыв. геометрическое место точек,для которых разность расстояний от двух фиксированных точек плоскости, называемых фокусами, есть постоянная величина.Параболой назыв.геометрическое место точек,для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом,равно расстоянию до некоторой фиксированной прямой,называемой директрисой. |
|
||||
|
2 Эллипс. F1, F2 – фокусы. F1 = (c; 0); F2(-c; 0) с – половина расстояния между фокусами; a – большая полуось,называемая эксцентриситетом эллип b – малая полуось. Фокусное расстояние и полуоси эллипса связаны соотношением:a2 = b2 + c2. В
случае, если точка М находится на
пересечении эллипса с вертикальной
осью, r1
+ r2
= 2
|
r1 + r2 = 2a. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом. Е = с/a. Т.к. с < a, то е < 1.
Величина
k
= b/a
называется коэффициентом
сжатия эллипса,
а величина 1 – k
= (a
– b)/a
называется сжатием
эллипса.
Коэффициент сжатия и эксцентриситет
связаны соотношением: k2
= 1 – e2.
Если a
= b
(c
= 0, e
= 0, фокусы сливаются), то эллипс
превращается в окружность.Если для
точки М(х1,
у1)
выполняется условие:
|
|
||||
|
22.Кривые второго порядка на плоскости:эллипс, гипербола,парабола. r1 = a – ex, r2 = a + ex Выше
было показано, что r1
+ r2
= 2a.
Кроме того, из геометрических соображений
можно записать:
После
возведения в квадрат и приведения
подобных слагаемых:
Аналогично доказывается, что r2 = a + ex. Эллипс определен ур-ем и a>b,то прямые x = a/e; x = -a/e называются директрисами эл. Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.
|
Г лениюr1 – r2=2a. F1, F2 – фокусы гиперболы. F1F2=2c.Выберем на гиперболе произвольную точку М(х, у). Тогда:
|
|
||||
|
22.Кривые второго порядка на плоскости:эллипс, гипербола,парабола. обозначим
с2
– а2
= b2
(геометрически эта величина – меньшая
полуось)
Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат. Ось 2а называется действительной осью гиперболы.
Асимптота кривой γ, имеющей бесконечную ветвь — прямая, обладающая тем свойством, что расстояние от точки γ кривой до этой прямой стремится к нулю при движении её вдоль ветви к бесконечности. |
О
|
|
||||
|
22.Кривые второго порядка на плоскости:эллипс, гипербола,парабола. Парабола.
Расположим начало координат посередине между фокусом и директрисой. Величина р (расстояние от фокуса до директрисы) называется параметром параболы. Выведем каноническое уравнение параболы. Из геометрических соотношений: AM = MF; AM = x + p/2; MF2 = y2 + (x – p/2)2 (x + p/2)2 = y2 + (x – p/2)2 x2 +xp + p2/4 = y2 + x2 – xp + p2/4 y2 = 2px-каноническое ур-ие параболы
|
Уравнение директрисы: x = -p/2. |
|
||||
|
23.Общие ур-ие кривых второго порядка на плоскости. Инварианты кривых второго порядка на плоскости.Классификация и виды каноническихь ур-ий(9)кривых второго порядка. Кривая второго порядка может быть задана уравнением Ах2 + 2Вху + Су2 + 2Dx + 2Ey + F = 0 Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.
1)
2)
3)
|
4)a2x2 – c2y2 = 0 – уравнение двух пересекающихся прямых. 5)y2 = 2px – уравнение параболы. 6)y2 – a2 = 0 – уравнение двух параллельных прямых. 7)y2 + a2 = 0 – уравнение двух “мнимых” параллельных прямых. 8)y2 = 0 – пара совпадающих прямых. 9)(x – a)2 + (y – b)2 = R2 – уравнение окружности. Линия,которая в некоторой декартовой системе координат определяется ур-ем второй степени, назыв.линией второго порядка. Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
в котором по крайней мере один из коэффициентов
|
|
||||
|
23.Общие ур-ие кривых второго порядка на плоскости. 1. 2.
3. инвариант относительно поворота системы координат 4.
|
Классификация кривых второго порядка. Невырожденные
кривые.
Кривая второго порядка называется
«невырожденной», если Могут возникать следующие варианты: Э Окружность (частный случай эллипса) — при условии
Мнимый Эллипс (пустое множество) — при условии D Гипербола — при условии D<0 Парабола — при условии D=0 В Точка— при условии D>0 (вырожденный эллипс) Пара пересекающихся прямых— при условии D<0 Пара параллельных прямых— при условииD=0 и B<0 Прямая (две слившихся параллельных прямых) — при условии D=0 и B=0 Пара мнимых параллельных прямых— при условии D=0 и B>0 |
|
||||
|
24.Поверхности второго порядка.Эллипсоиды,гиперболоиды,Параболоиды, цилиндры,конусы.Канонич.ур-я.Инварианты. Поверхность второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлет-ют уравнению вида a11x2 + a22y2 + a33z2 + 2a12xy + 2a23yz + 2a13xz + 2a14x + 2a24y + 2a34z +a44= 0 в
котором по крайней мере один из
коэффициентов a11, a22, a33, a12, a23, a13 отличен
от нуля. Эллипсо́ид
– поверхность,которая в некоторой
системе декартовых прямоугольных
координат определяется ур-ем
Велечины a,b,c суть полуоси эллипсоида.Если a=b-ось вращения будет Oz,если a=b<c эл-д назыв.вытянутым. При a=b>c-сжатым.Если a=b=c,эл-д-сфера. Гиперболоид назыв.поверхности,которые в некоторой системе декартовых прямоугольных координат определ.ур-ми: |
Параболо́идами назыв.поверхности,которые в некоторой системе декартов.координат определ.ур-ями.
,где p,q-положит.числа назыв.параметрами параболоида.
Конической поверхностью или конусом назыв.поверхность,которая описывает движущейся прямой(образующей) при условии,что эта прямая проходит через постоянную точку s и пересекает некоторую определенную линию L.Точка S назыв.вершиной конуса,линия L-направляющей. |
|
||||
|
24.Поверхности второго порядка.Эллипсоиды,гиперболоиды,Параболоиды, цилиндры,конусы.Канонич.ур-я.Инварианты.
Цилиндрической поверхностью,или цилиндром,назыв. поверхность,которая описывается движущейся прямой (образующей)при условии,что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляюшую).
|
Поверхности второго порядка, поверхности, декартовы прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению 2-й степени a11x2 + a22y2 + a33z2 + 2a12xy + 2a23yz + 2a13xz + 2a14x + 2a24y + 2a34z + a44 = 0(*) Уравнение (*) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую Поверхности второго порядка В зависимости от значений коэффициентов общего уравнения (*) оно может быть преобразовано с помощью параллельного
|
|
||||
|
24.Поверхности второго порядка… переноса и поворота системы координат к одному из 17 приведённых ниже канонических видов, каждому из которых соответствует определённый класс Поверхности второго порядка Среди них выделяют пять основных типов поверхностей. Именно, 1) эллипсоиды
2) гиперболоиды:
|
3) параболоиды (p > 0, q > 0):
4) конусы второго порядка:
|
|
||||
|
24.Поверхности второго порядка… 5) цилиндры второго порядка:
Перечисленные Поверхности второго порядка относятся к т. н. нераспадающимся Поверхности второго порядка; распадающиеся Поверхности второго порядка:
|
х2 = а2 — пары параллельных плоскостей, х2 = —а2 — пары мнимых параллельных плоскостей, х2 = 0 — пары совпадающих плоскостей. Для Поверхности второго порядка установлена аффинная и проективная классификация. Две Поверхности второго порядка считают принадлежащими одному аффинному классу, если они могут быть переведены друг в друга некоторым аффинным преобразованием (аналогично определяются проективные классы Поверхности второго порядка). Каждому аффинному классу соответствует один из 17 канонических видов уравнения Поверхности второго порядка Проективные преобразования позволяют установить связь между различными аффинными классами Поверхности второго порядка Это объясняется тем, что при этих преобразованиях исчезает особая роль бесконечно удалённых элементов пространства. Например, эллипсоиды и двуполостные гиперболоиды, различные с аффинной точки зрения, принадлежат одному проективному классу Поверхности второго порядка. |
|
||||
|
25.Линейные операторы в линейном пространстве. Матрица линейного оператора. Если
задан закон(правило), по которому
каждому вектору х
пространства Rn
ставится в соответствие единственный
ветор y
пространства
Rm,то
говорят,что задан оператор (преобразование,
отображение)
1. 2.
Вектор
y= Если пространства Rn и Rm совпадают, то оператор A |
отображает пространство Rn в себя. Матрица
А=(aij)
(i,j=1,2,...n)
назыв.матрицей оператора
в базисе l1,l2,...ln,а ранг r матрицы A-рангом оператора
Действия над линейными операторами: С (А+В)(х)=А(х)+В(х). Произведен.линейн.оператора А на число лямбда назыв.оператор лямбдаА,определ. равенством : (лямбдаА)(х)=лямбда(А(х)). Произведением лин.операт-ов А и В назыв.оператор АВ определ-ый равенством (АВ)(х)=А(В(х)). |
|
||||
|
26.Преобразование координат вектора при переходе к новому базису. Изменение координат вектора при изменении базиса Пусть
в n-мерном
линейном пространстве L
выбран базис l1,l2,...ln
который мы будем для удобства называть
"старый" и другой базис Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно "связать" друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису |
Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса
Эта
матрица называется матрицей перехода
от старого базиса к новому. Матрица
перехода всегда невырождена, то есть
|
|
||||
|
26.Преобразование координат вектора при переходе к новому базису. где справа стоит произведение матрицы перехода S на матрицу-столбец. Матрица
А и А`линейного оператора
А`=С(«в –1степени»)АС,где С-матрица перехода от старого базиса к новому. При
воздействии линейного оператора
|
Левую часть полученного выражения в соответствии с (2), имеем: СУ`=АСХ` или У`=C(«в –1степени»)АСX` |
|
||||
|
27.Собственные векторы и собственные значения линейного оператора. Характеристический многочлен линейного оператора. В
Собственный
вектор под действием оператора
Определитель
|A
- лямбдаЕ| является многочленом n-й
степени относительно лямбды.Этот
многочлен называется характеристическим
многочленом оператора
|
|A - лямбдаЕ|=
-характеристическим
ур-ием оператора
А. Характеристический многочлен линейного оператора не зависит от выбора базиса.
Матрица
оператора
Если оператор имеет n попарно различных собственных значений,то отвечающие им собственные векторы линейно независимы , и матрица этого оператора в соответствующем базисе имеет диагональный вид. |
|
||||
|
|
№1. Матрицы, виды, действия с ними. Задачи. Матрицей размера mn назыв прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа составляющие матрицу назыв элементами матрицы. Их обозначают aij, где i-номер строки, а j-номер столбца. Виды матриц: Матрица, состоящая из одной строки, называется матрицей (вектором)-строкой, а из одного столбца-матрицей(вектором)-столбцом. А=(а11а12,..,а1n)-матрица-строка; В=b11 матрица-столбец. Матрица называется квадратной b21 n-го порядка,если число ее строк равно числу столб … и равно n. Элементы матрицы aij, у которых bm1 номер столбца равен номеру строки (i=j), называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы а11,а22,..аnn. Если все недиагональные элементы квадратной матрицы равны нулю,то матрица |
называется диагональной. Если у диагональной матрицы n-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n-го порядка, она обозначается буквой Е. Произведение матрицы А на число λ называется матрица В= λА, элементы которой bij=λ aij для i=1.2....m; j=1.2…n. Общий множитель всех элементов матрицы можно выносить за знак матрицы. Суммой двух матриц А и В одинакового размера mхn называется матрица С=А+В, элементы которой сij= aij+ bij для i=1.2....m, j=1.2…n(т.е матрицы складываются поэлементно). Разность двух матриц одинакового размера определяется через предыдущие операции: А-В=А+(-1) В. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Произведением матриц А mхk х B kхn называется такая матрица С mхn, каждый элемент которо |
||||
|
|
№1. Матрицы, виды, действия с ними. Задачи. сij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В: сi j = ai 1b1 j+ ai 2 b2 j+ ai k b k j, i=1.2....m, j=1.2…n. Свойства: 1)А+В=В+А 2)(А+В)+С=А+(В+С) 3) λ(А+В)= λА+ λВ 4)А(В+С)=АВ+АС 5)(А+В)С=АС+ВС 6) λ(АВ)=( λА)В=А(λВ) 7)А(ВС)=(АВ)С Целой положительной степенью Аm (m>1) квадратной матрицы А называется произведение m матриц, равных А. Транспонирование матрицы-переход от матрицы А к матрицы А’ или Ат, в которой строки и столбцы поменялись местами с сохранением порядка. Свойства: 1)(А’)’=А 2)( λА)’=λ А’ 3)(А+В)’ = А’+В’ 4)(АВ)’= В’ А’ Задача: |
Найти
произведение матриц А =
|
||||
|
|
№2.Определители квадратных матриц. Св-ва опр. Миноры и алгеб дополнения. Методы вычисления опр. Элемент а11 называется опред-ем 1-го порядка. Опр 2-го порядка назыв число, которое вычисляется по формуле: а11а22- а12 а21. Опр 3-го порядка назыв число, которое вычисляется по формуле: а11 а22 а33+ а12 а23 а31+ а21 а32 а13- а31 а22 а13- а12 а21 а33- а32 а23 а11. Опр квадратной матрицы n-го порядка, назыв число, равное алгебр-ой сумме n членов, каждый из которых явл произведением n элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем знак каждого члена опред-ется как (-1)r(j) , где r(j)-число инверсий в перестановке j из номеров столбцов элементов матрицы, если при этом номера строк записаны в порядке возрастания: (инверсия в перестановке j это наличие пары чисел, в которой большее число предшествует меньшему). |
׀А׀=׀ а11 а12… а1n׀=∑j(-1) r(j) а1j1 х а2j2 х .. аnjn. Минором Мi j ׀ а21 а22… а2n׀ элемента аij матрицы n-го порядка назы׀ аn1 аn2… аnn׀ определитель матрицы (n-1)-го порядка, полученной из матрицы А вычеркиванием i-й строки и j-го столбца. Алгебраическим дополнением Аi j элемента аij матрицы n-го порядка назыв его минор, взятый со знаком (-1) i+j . Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки(столбца) на их алгебраические дополнения: ׀А׀= аi1А i1+ аi2А i2+ аin А in (разложение по элементам i-й строки; i=1.2.... n. Свойства опред: 1)Если какая-либо строка(столбец) матрицы состоит из одних нулей, то ее определитель равен 0. 2)Если все элементы какой-либо строки(столбца) матрицы умножить на число λ, то ее опред умножится на это число λ. 3)При транспонирова- нии матрицы ее опред не изменяется:׀А’׀= ׀А׀. |
||||

 ектор
an
назыв.линейн.комбинацией
векторов
ектор
an
назыв.линейн.комбинацией
векторов
 общем случае утверждение "вектор
общем случае утверждение "вектор
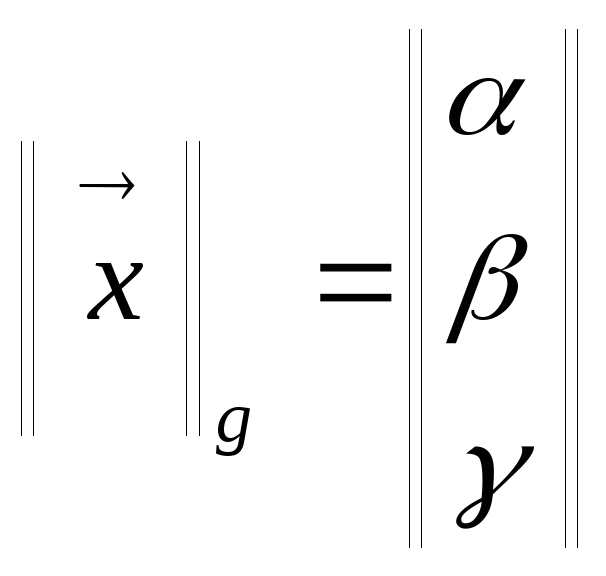 .
.

 называется основной матрицей
системы, а матрица
называется основной матрицей
системы, а матрица
 - расширенной матрицей этой
системы.
- расширенной матрицей этой
системы.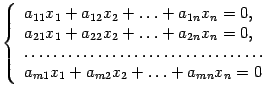
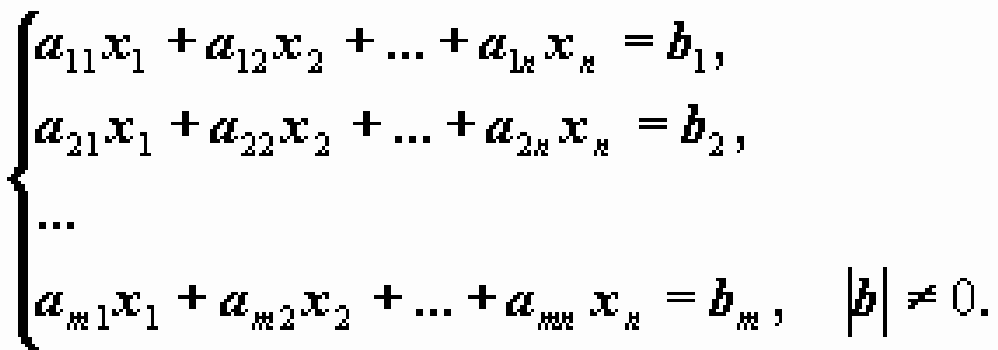
 еопределенная
и имеет бесконечное множество решений.
еопределенная
и имеет бесконечное множество решений.


 Зависимые несовместная
(множ.реш.)
Зависимые несовместная
(множ.реш.)

 инейных
инейных Системы
Сис-ма определенная
Системы
Сис-ма определенная ля
получения системы при m=n
в общем виде предположи,что
квадратн.матрица системы An*m
невырожденная,т.е.её определитьель
|A|=0.В
этом случае существ.обратная матрица.
Умножая слева обе части матричного
равенства на матрицу обратную,получим
…
ля
получения системы при m=n
в общем виде предположи,что
квадратн.матрица системы An*m
невырожденная,т.е.её определитьель
|A|=0.В
этом случае существ.обратная матрица.
Умножая слева обе части матричного
равенства на матрицу обратную,получим
…



 еорема
Крамера.Пусть
-определитель матрицы системы А,а
j-определитель
матрицы,получаемый из матрицы А заменой
j-го
столбца столбцом свободных членов.
Тогда,если =0 ,то система имеет
единственное решение,определяемое
по формулам:Xj=
j
/ , (j=1,2…n)
еорема
Крамера.Пусть
-определитель матрицы системы А,а
j-определитель
матрицы,получаемый из матрицы А заменой
j-го
столбца столбцом свободных членов.
Тогда,если =0 ,то система имеет
единственное решение,определяемое
по формулам:Xj=
j
/ , (j=1,2…n)


 2
Y2
Z2
2
Y2
Z2 линейно
независимы.
линейно
независимы.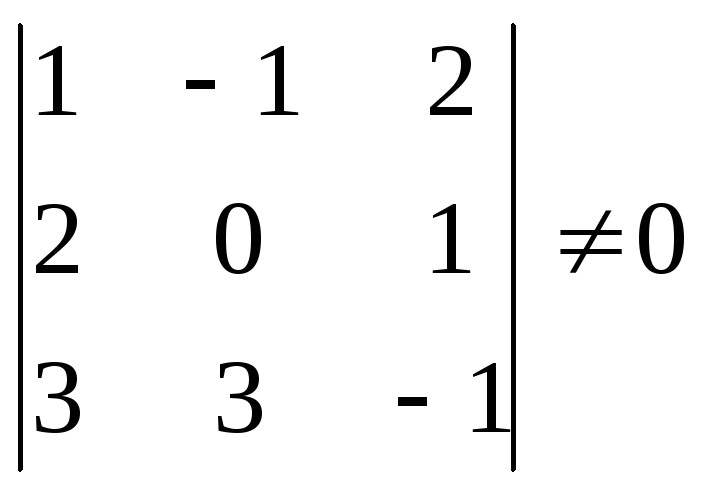

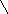 =4 =0
=4 =0 Для
решения этой системы воспользуемся
методом Крамера.
Для
решения этой системы воспользуемся
методом Крамера.


 - уравнение
эллипса.
- уравнение
эллипса.
 2.Кривые
второго порядка на плоскости:эллипс,
гипербола,парабола.
2.Кривые
второго порядка на плоскости:эллипс,
гипербола,парабола.
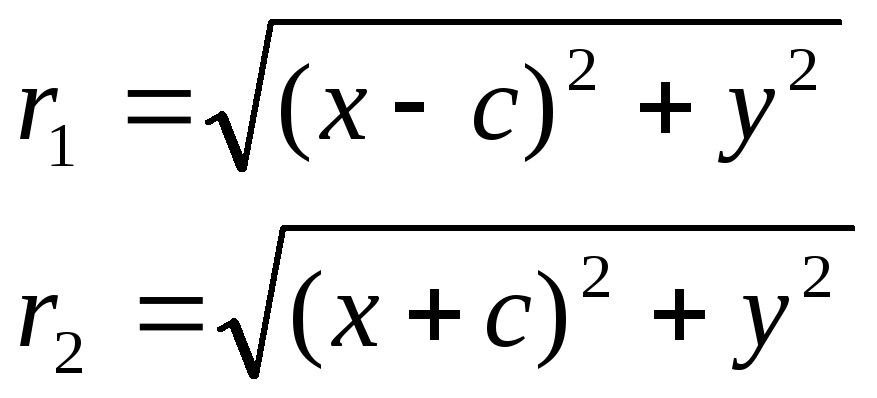
 ипербола.
По опреде-
ипербола.
По опреде-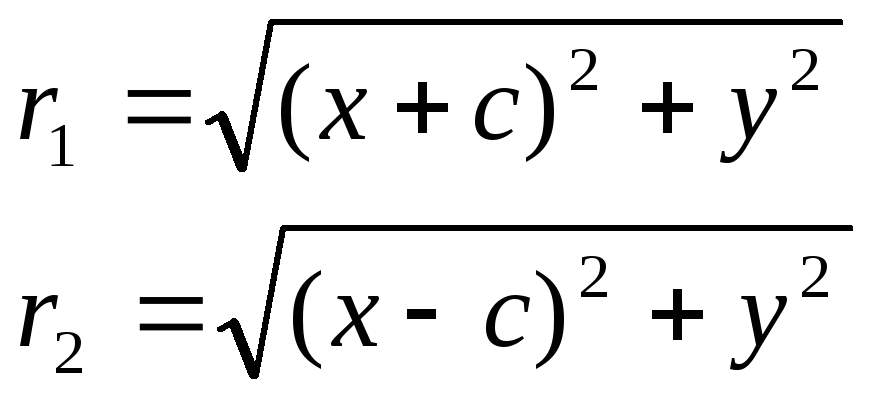
 Ось
2b
называется мнимой осью гиперболы.
Гипербола имеет
две асимптоты, уравнения которых
Ось
2b
называется мнимой осью гиперболы.
Гипербола имеет
две асимптоты, уравнения которых тношение
тношение

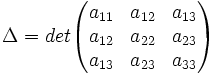
 ллипс
— при условии D>0
и I
<0
ллипс
— при условии D>0
и I
<0 =0
и I
>0
=0
и I
>0 ырожденные
кривые. Кривая
второго порядка называется «вырожденной»,
если =0
ырожденные
кривые. Кривая
второго порядка называется «вырожденной»,
если =0
 уммой
двух линейных операторов
уммой
двух линейных операторов
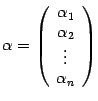 а в новом
а в новом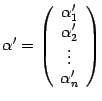
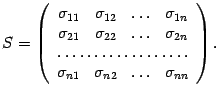
 ектор
х=0 назыв.собственным
вектором линейного оператора
ектор
х=0 назыв.собственным
вектором линейного оператора
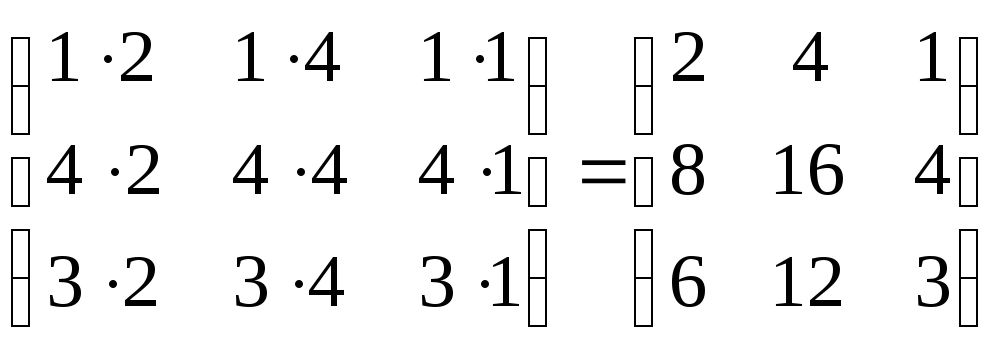 .
.