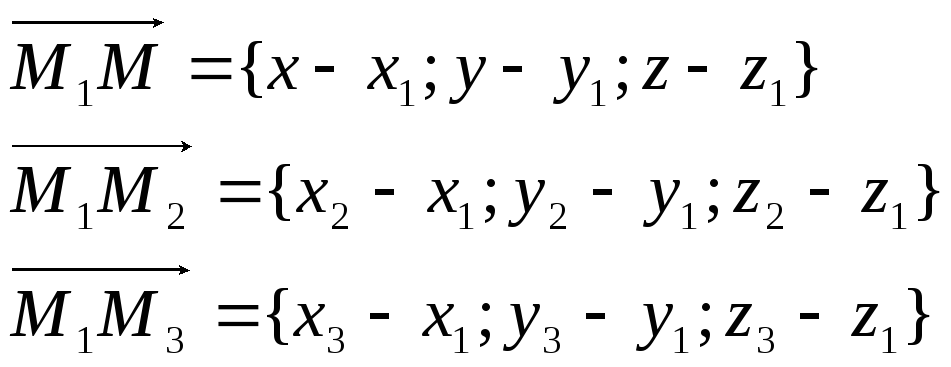МАТАН (шпоры)

№2.Определители квадратных матриц. 4)При перестановке двух строк(столбцов) матрицы ее опред меняет знак на противоположный. 5)Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен 0. 6)Если элементы двух строк (столбцов) матрицы пропорциональны, то ее опред равен 0. 7)Сумма произведений элементов какой-либо строки(столбца) матрицы на алгебр дополнения элементов другой строки (столбца) этой матрицы равна 0, т.е ∑ ⁿ_S=1 а_isА_js=0, при i не равное j. 8)Опред матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки(столбца), предварительно умноженные на одно и то же число. 9)Сумма произведений произвольных чисел b_1, b_2, … b_n на алгебр дополнения элементов любой строки(столбца) равна опред матрицы, полученной из данной заменой элементов этой строки

(столбца) на числа b_1, b_2, … b_n. 10)Опред произведения двух квадратных матриц равен произведению их опред: ׀С׀= ׀А׀x׀В׀ где С=АхВ, А и В-матрицы n-го порядка.

№3.Обратная матрица. Критерии существования обр матрицы. Алгоритм вычислен обр матр. Матрица А^-1называется обратной по отношению к квадратной матрице А, если при умножении этой матрицы на данную как справа, так и слева получается единичная матрица: А^-1хА=Ах А^-1=Е. Необходимое и достаточное условие существования обратной матрицы. Обратная матрица А^-1 существует( и единственна) тогда и только тогда, когда исходная матрица невырожденная. Невырожденной матрицей назыв матрица если ее определитель отличен от нуля. Алгоритм вычисления обратной матрицы. 1)Находим опред исходной матрицы. Если опред=0, то матрица А- вырожденная и обратной матрицы А^-1 не существует. Если опред не равен нулю, то матрица А-невырожденная и обратн матрица существует. 2)Находим матрицу А’ транспонированную к А.

3)Находим алгебраические дополнения элементов транспонированной матрицы А’ij=Аji (i=1.2…n; j=1.2…n) и составляем из них присоединенную матрицу А^~ : aij^~ =А’ij ₌ Аji (i=1.2…n; j=1.2…n). 4)Вычисляем обратную матрицу по формуле А^-1 =1/ ׀А׀x А^~ 5)Проверяем правильность вычисления обратной матрицы А^-1 , исходя из ее определения А^-1хА= Е

№6. Определение геометрического вектора. Нулевой, противоположный вектор, коллинеарные и компланарные векторы. Равенство векторов. Действия с векторами. Направленный отрезок принято назыв геометрич вектором. Если начало и конец вектора совпадают, то такой вектор называют нулевым. Противо-ным вектором –а назыв произведение вектора а на число (-1). Колли-рными назыв векторы лежащие на одной прямой или на параллельных прямых,. Свойства колин: 1)нулевой вектор колинеар любому вектору. 2)Скалярное произ-е колли-ых векторов ахв=+-ав равно произведению длин векторов (взятых со знаком – если противо-но направ). 3)Векторное произведение векторов [ав]=0 4)Колл-ные векторы линейно зависимы. Т е сущ число λ такое, что а= λв, если в не равно о. 5)На пл-ти неколлинеарные векторы образуют базис с=х1а+х2в, (х1,х2)-координаты

с в данном базисе. Векторы назыв компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Признак компл: если вектор с можно разложить по векторам а и в, т е представить в виде с=ха+ув, где х и у некоторые числа, то векторы а, в и с комплан. Св-ва компл: 1)Тройка векторов, содерж-ая пару колинеарн векторов компл-на. 2)Смеш-ое произведение компланар векторов =0. Вект назыв равными, если они имеют одинаковые длины, лежат на пара-ых прямых или на одной прямой и направлены в одну сторону. Суммой двух векторов а и в назыв вектор с=а+в, начало которого совпадает с началом вектором а, а конец с концом вектора в при условии, что начало вектора в совпадает с концом вектора а.Ели векторы а и в приведены к общему началу и на них построен пара-амм, то сумма а+в есть вектор, совпадающий с диагональю этого парал-ма.

№15.Опр скал-ого произв-я. Его св-ва. Вывод формулы скал пр. Признак ортогональности векторов. Ортог проекция вект-а на ось. Вычисление угла между векторами. Число равное произведению модулей векторов на косинус угла между ними назыв скаляр произ-ие двух вект-ов. Св-ва: 1)аха≥0, аха>0 при Ане равном о. 2)ахв=вха(переем закон) 3)(kха)хв=k(ахв)(сочет-й закон). 4)(а+в)хс=ахс+вхс(распред-й закон). Вывод формулы скал пр: Дано а и в не равн о и не коллинеарные. Тогда в+с=а, с др стороны с=а-в. По теореме косинусов с² =а² +в² -2ав cosi. (а-в) ² = а² +в² -2ав. 2ав= а² +в²-(а-в) ² . ав=1/2(а² +в²-(а-в) ²). а-в (х1-х2;у1-у2;z1-z2) ׀а׀ =√х1²+у1²+ z1² ׀в׀ =√х2²+у2²+ z2² (а-в)= √(х1-х2) ²+(у1-у2) ²+(z1-z2) ² –х1+2х1х2+х2. ахв=1/2(х1² +у1² +х2² +у2² +z1² +z2² – (х1-х2) ² -(у1-у2)² –(z1-z2) ²

Ахв=1/2(2х1х2+2у1у2+2 z1z2) ахв=х1х2+у1ху2+ z1хz2. Если скалярное произвед равно о, то векторы ортогональны. Угол между векторами а(х1,у1, z1) и в(х2,у2,z2) вычисляется по формуле cosi.=ав/ ׀а׀ ׀в׀. пр_хS=х cosα+уcosβ+ zcosγ-проекция произвольного вектора на ось.

№16.Правые и левые тройки геометр-их вект-ов. Опред вектор-ого произв-я.Его св-ва.Признак коллин-сти. Тройка некомпланарных векторов а,в,с назыв правой, если ее векторы, приведены к общему началу и располагаются в порядке нумерации аналогично тому, как расположен большой, указательный и средний пальцы правой руки. Если векторы а,в,с расположены анологично тому, как расположены большой, указательный и средний пальцы левой руки, то тройка этих векторов называется левой. Векторным произведением вектора а на вектор в называется вектор, обозначаемый символом [ав] и определяемый следующими тремя условиями: 1)модуль вектора [ав] равен / ׀а׀ ׀в׀ sinα, где α-угол между векторами а и в 2)вектор [ав] перпендикулярен к каждому из векторов а

и в 3)направление вектора [ав] соответствует правилу правой руки. (т е если векторы приведены к общему началу. То вектор [ав] должен быть направлен так, как направлен средний палец правой руки, большой палец-а, а указательный в. Св-ва: 1)векторное произведение зависит от порядка сомножителей: [ав]=- [ва] 2)модуль векторного произведения равен площади пар-ма, построенного на векторах а и в. 3)векторное произведение превращается в нуль, если векторы а и в коллинеарные. 4)векторное произведение при а(х1,у1,z1) и в(х2,у2,z 2)может быть вычислено по формуле: [ав]=i j k

х1у1z1

х2у2z 2 Признакjv коллин-сти 2-х векторов а(х1,у1, z1) и в(х2,у2,z2) явл пропорциональность их координат: х2/х1=у2/у1=z2/ z1.

№17.Определение смешанного произведения трех векторов. Его св-ва. Признак компланарности 3 векторов. Нахождение объема тетраэдра. Число равное векторному произведению [ав] умноженному скалярно на вектор с назыв смешанным произведением. Св-ва: 1)авс=[ав]с 2)смешанное произведение авс равно объему параллелепипеда, построенного на векторах а в с, взятому со знаком +, если тройка а в с правая и со знаком -, если эта тройка левая. 3)если векторы а,в,с компланарны, то смешанное произведение а,в,с=о. 4)авс= х1у1z1 где а(х1,у1, z1)

х2у2z2 в(х2,у2,z2

х3у3z3 с(х3,у3,z3)

Признак компл: если вектор с можно разложить по векторам а и в, т е представить в виде с=ха+ув, где х и у некоторые числа, то векторы а, в и с комплан.

№18.Общее уравнение прямой и его исследование. Уравнение вида Ах+Ву+С=0 назыв общим уравнением прямой. К(угловой коэф-ент-тангенс угла наклона прямой к Ох)=-А/В. Рассмотр-им уравнение первой степени с двумя переменными в общем виде, в котором коэф-ты А и В не равны одновременно нулю, т е А² +В² не равно о. 1)Пусть В не равно о. Тогда уравнение общее можно записать в виде у=-А/Вх-С/В. Обозначим к=-А/В, в= С/В. Если А и С не равны о, то получим у=кх+в(уравн прям с угловым коэф-ом). Если А не равно о, а С равно, то у=кх(уравнение прямой проходя-ей через начало коорди-ат). Если А=о, а С не равно о, то у=в(уравнение прямой, парал-ой Оу). Если А=0, С=0, то у+0(уравнение Ох). 2)Пусть В=о, А не равно о. Тогда уравнение общее примет вид х=-С/А. Обозначим а=-С/А. Если С не равно о, то получим х=а(уравнение

Прямой, парал-ой Оу). Если С=0, то х=0(уравнение Оу). Т.е при любых значениях коэффиентов А, В(не равных одновременно нулю) и С уравнение есть уравнение некоторой прямой линии на плоскости Оху. Уравнение у=кх+в назыв уравнением прямой с угловым коэф-от. Где к-угловой коэф-ент, в-величина отрезка, который отсекает прямая на Оу, считая от начала координат. Рисунок. Пусть прямая пересекает Оу в точке В(0,в) и образует с Ох угол α (0< α <п/2). Возьмем на прямой произвольную точку М(х,у). Тогда тангенс угла α наклона прямой найдем из прямоугольного треугольника MBN: tg α= MN/NB=у-в /х. Введем угловой коэф-ент прямой к= tgα, получим к=у-в/х. у=кх+в. Формула остается справедливой и для случая п/2< α<п. Частные случаи: 1)Если в=о, то получаем у=кх- уравнение прямой, проходящей через начало координат и образующей при к= tgα>0 острый

№18.Уравнением прямой с угловым коэф-от.

угол α с осью Ох, а при к= tgα<0 –тупой угол. В частности, уравнение биссектрисы 1 и 3 коорд-ых углов имеет вид у=х (так как к= tgП/4=1), а уравнение биссектрисы 2 и 4 координат-ых углов у=-х(к= tg 3П/4=-1). 2)Если α=0, то к= tg0=0, и уравнение прямой, параллельной Ох, имеет вид у=в, а самой оси Ох- вид у=0. 3)Если α=П/2, то прямая перпендикулярна Ох и к= tg П/2 не существует, т е вертикальная прямая не имеет углового коэф-ента. Предположим, что эта прямая отсекает на оси Ох отрезок, равный а. Очевидно, что уравнение такой прямой х=а (так как абцисса любой точки прямой равна а), а уравнение Оу есть х=0.

Уравнение прямой в отрезках. Найдем уравнение прямой по заданным отрезкам а и в не равной 0, отсекаемым на осях координат. Используя уравнение прямой, проходящей через точки А(а;0) и В(0;в), примет вид у-о/в-0 = х-а/0-а или после преобразований х/а+у/в=1-уравнение прямой в отрезках.

Уравнение прямой, проходящей через две данные точки. Пусть даны две точки М1(х1;у1) и - М2(х2;у2) и х1не равен х2, у1 не равен у2. -- Для составления уравнения пучка прямых, - проходящ-их через точку М1: у-у1=к(х-х1) - Т.к точка М2(х2,у2) лежит на данной -- - прямой, то чтобы выделить ее из пучка, подставим координаты точки М2 в уравнение пучка у2-у1=к(х2-х1) и найдем угловой коэф-ент прямой к=у2-у1/х2-х1. Теперь уравнение искомой

№18. Уравнение прямой, проходящей через две данные точки. Искомой прямой примет вид у-у1=у2-у1/х2-х1 (х-х1) или у-у1/у2-у1=х-х1/х2-х1. Взаимное расположение прямых на плоскости. L1: А1х+В1у+С1=0 L2: А2х+В2у+С2=0 1)Когда прямые пар-ны. L1 ׀׀ L2 следовательно А1/А2=В1/В2не равное С1/С2. Если будет равенство то прямые совпадут. 2) L1 перпендикулярна L2(скалярное произв =о), следовательно А1А2+В1В2=0. Если у=к1х+в1 у=к2х+в2 к1= к2-прямые пар-ны (L1 ׀׀ L2). Если L1перпенд-на L2 следоват к1к2=-1. Угол между прямыми. Пусть заданы две прямые у=к1х+в1 у=к2х+в2 и требуетвся определить угол φ между ними. φ=α2-α1, причем к1= tg α1, к2= tg α2, α1не равно П/2, α2 не равно П/2. Тогда tg φ= tg(α2- α1)= tg α2- tg α1/1+ tg α1 tg α2 или tg φ=к2-к1/1+к1к2. где угол φ получается поворотом прямой к

Прямой против часовой стрелки. Условия пар-сти и перпендикулярности прямых. Если прямые у=к1х+в1 и у=к2х+в2 пар-ны, то угол φ=0 и tg φ=0, откуда из формулы tg φ=к2-к1/1+к1к2 следует к1=к2. И наоборот, если к1=к2, то по формуле tg φ=к2-к1/1+к1к2 tg φ=0 и φ=0. Т.е равенство угловых коэфиц-ов явл необходимым и достаточным условием параллельности двух прямых. Для перпендикулярности прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку. Условием параллельности прямых, заданных общими уравнениями, явл пропорциональность коэффициентов при переменных. (А1/А2=В1/В2). Условием перпендикулярности двух прямых, заданных

№18,Общими уравнениями, явл равенство нулю суммы произведений коэф-ов при переменны х и у. (А1А2+В1В2=0). Расстояние от точки до прямой. Пусть даны точка М(х0;у0) и прямая Ах+Ву+С=0. Под расстоянием от точки М до прямой АВ понимается длина перпендикулярна d=MN, опущенного из точки М на прямую АВ. Для опред-я расстояния d необходимо: а)составить уравнение прямой MN, перпендикулярной данной и проходящей через М0(х0,у0) б)найти точку N(х1,у1) пересечения прямых, решив систему уравнений этих прямых в) по формуле d=√ ׀АВ׀² = √(х2-х1) ² +(у2-у1) ² . определить расстояние между двумя точками, т е найти d= MN. В результате преобразования получим d=׀Ах0+Ву0+С׀ / √А²+В² . Нормальный вектор-это

любой не нулевой вектор перпендикулярный данной

прямой. Направляющий вектор- это любой не нулевой вектор парал-ый данной прямой. Каноническое уравнение х-х0/m=y-y0/n. Параметрическое уравнение х-х0/m=y-y0/n=t. Нормальное уравнение прямой на плоскости: хcosα+уcosβ-р=0 при р>0

№4. Умножение матриц. Транспонирование произведения матриц. Св-ва опред-ля от произведения матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Произведением матриц А _mхk х B _kхn называется такая матрица С _mхn, каждый элемент которой с_ij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В: с_{i j =} a_{i 1}b_{1 j}+ a_{i 2} b_{2 j}+ a_{i k} b _k j, i=1.2....m, j=1.2…n. Свойства: 1)А+В=В+А 2)(А+В)+С=А+(В+С) 3) λ(А+В)= λА+ λВ 4)А(В+С)=АВ+АС 5)(А+В)С=АС+ВС 6) λ(АВ)=( λА)В=А(λВ) 7)А(ВС)=(АВ)С Транспонирование матрицы-переход от матрицы А к матрицы А’ или А^т, в которой строки и столбцы поменялись местами с сохранением порядка. Свойства: 1)(А’)’=А 2)( λА)’=λ

А’ 3)(А+В)’ = А’+В’ 4)(АВ)’= В’ А’

№5. Решение СЛАУ с помощью обратной матрицы.

Для получения системы при m=n в общем виде предположи,что квадратн.матрица системы An*m невырожденная,т.е.её определитьель |A|=0.В этом случае существ.обратная матрица. Умножая слева обе части матричного равенства на матрицу обратную,получим …

№19. Общее уравнение плоскости. Пусть Q проходит через точку М0(х0,у0,z0) перпендикулярно вектору n=(А,В,С). Этими условиями определяется единственная плоскость в пространстве Охуz. Вектор , n назыв нормальным вектором плоскости Q. Возьмем в плоскости Q произвольную точку М(х,у,z). Тогда вектор М₀М==(х-х₀. у-у₀, z- z₀₎ будет перпендикулярен вектору n=(А,В,С). Следовательно, скалярное произведение этих векторов равно 0, т.е (n, М₀М)=0. Полученное уравнение представим в координатной форме: А(х-х0) + В(у-у0) + С(z- z0)=0 – данное уравнение представляет уравнение плоскости, перпендикулярной данному вектору n=(А,В,С) и проходящей через данную точку М0(х0,у0, z0). Уравнение плоскости, записанное в виде Ах+Ву+Сz+D=0 (где D= -А х₀ -В у0-С z0) назыв-ся

общим уравнением плоскости. Условия парал-ти и перпен-ти плоскостей определяются условиями коллинеарности и перпендикулярности нормальных векторов n1=(А1,В1,С1) и n2=(А2,В2,С2). Условием пар-ости двух плоскостей явл пропорциональность коэффициентов при одноименных переменных А1/А2=И1/В2=С1/С2, а условием их перпендикулярности

А1А2+В1В2+С1С2=0. Если уравнение плоскости Ах+Ву+Сz+D=0 ни один из коэффициентов А, В, С, D не равен нулю, то это уравнение может быть преобразовано к виду х/а+у/в+z/с=1, где а=- D/А, в+- D/В, с=- D/С суть величины отрезков, которые плоскость отсекает на координатных осях. Уравнение данное назыв уравнением плоскости в отрезках. Нормальным уравнением плоскости назыв-ся ее уравнение, написанное в виде хcosα+уcosβ+ z cosγ-р=0,

№19. Нормальным уравнением плоскости. где cosα, cosβ, cosγ-направляющие косинусы нормали плоскости, р- расстояние от начала координат до плоскости. При вычислении направляющих косинусов нормали следует считать, что она направлена от начала координат к плоскости. Расстояние от точки до плоскости. Пусть М*-какая угодно точка пространства, d – расстояние от нее до данной плоскости. Отклонение δ точки М* от данной плоскости назыв число + d, если точка М* и начало координат лежат по разные стороны от данной плоскости, и число – d, если они лежат по одну сторону от данной плоскости. Если точка М* имеет координаты х*,у*, z*, а плоскость задана нормальным уравнением хcosα+уcosβ+ z cosγ-р=0, то отклонение точки М* от этой плоскости дается формулой δ=х* cosα+у*cosβ+ z *cosγ-р. Очевидно, d= ׀δ׀. Уравнение плоскости Ах+Ву+Сz+D=0 приводится к

нормальному виду умножением на нормирующий множитель, определяемый формулой μ=+- 1/√А²+В²+С² знак нормирующего множителя берется противоположным знаку свободного члена нормируемого уравнения. Уравнение плоскости проходящей через три точки. Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.

Рассмотрим точки М₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃) в общей декартовой системе координат.

Для того, чтобы произвольная точка М(x, y, z) лежала в одной плоскости с точками М₁, М₂, М₃ необходимо, чтобы векторы были компланарны. ) = 0

№19.Уравнение плоскости проходящей через три точки. Таким образом,

Уравнение плоскости, проходящей через три точки:

№ 20. Каждый не равный нулю вектор, лежащий на данной прямой или пар-ый ей, назыв направляющим вектором этой прямой. Направляющий вектор произвольной прямой обознач а, а его координаты l.m.n. а=( l.m.n). Если известна точка М0 (х0,у,z0) прямой и направляющий вектор а=(l.m.n), то прямая может быть определенна (двумя) уравнениями вида х-х0/ l = у-у0/ m = z-z0/ n – каноническое уравнение прямой. Канонич уравн прямой проход-ие через данные точки М1(х1,у1,z1) и М2(х2,у,z2) имеют вид х-х1/ х2-х1 = у-у1/у2-у1= z-z1/z2-z1. Обозначим буквой t каждое из равных отношений в канонических уравнениях получим х-х0/ l = у-у0/ m = z-z1/ n = t. Отсюда х= х0+lt, у=у0+mt z=z0+nt –это параметрические уравнения прямой, проходящей через точку М0 в направлении вектора а=(l.m.n).

№7. Опред линейного векторного пространства. Линейная комбинация векторов. Линейное векторное пространство это множество элементов произвольной структуры для которых заданы условия равенства и две операции, а именно сложение этих элементов и умножение на число. Св-ва: 1)для любых х и у принадлежащих v 2)? (λх) принадлежит v.

Линейная комбинация векторов. Вектор аm назыв линейной комбинацией векторов а1,а2,,,аm-1 векторного пространства R если он равен сумме произведений этих векторов на произведение действительного числа. аm= λ1а+ λ2а2,,,,+ λ m-1а m-1.

№21. Взаимное расположение L и П. 1) L׀׀ П следовательно n перпендикулярен П 2) L перпендикулярна П следовательно n ׀׀ а 3) L принадлежит П 4) L пересекает П=М

Угол между L и П. cosα=( n, а) / ׀ n׀ ׀а׀ =sin φ , где а- направляющий вектор. Расстояние от точки L до v3. Если прямая r=r1+at, где t параметр а-направляющий вектор, то h= S/ ׀а׀ = ׀ (r0-r1, a) ׀ S- площадь пар-ма построенного наь векторах r0- r и а, приведенных к общему началу.

№1. Матрицы, виды, действия с ними. Задачи.

№2.Определители квадратных матриц

№3.Обратная матрица. Критерии существования обр матрицы. Алгоритм вычислен обр матр.

№4. Умножение матриц. Транспонирование произведения матриц. Св-ва опред-ля от произведения матриц.

№5. Решение СЛАУ с помощью обратной матрицы.

№6. Определение геометрического вектора. Нулевой, противоположный вектор, коллинеарные и компланарные векторы. Равенство векторов.

№7. Опред линейного векторного пространства. Линейная комбинация векторов.

8.Линейная зависимость и линейная независимость векторов.

9.Определение базиса и размерности линейн.пространства.

10.Определение базисного минора матрицы. Лемма.Ранг.Вычисление ранга.

11. Системы линейных алгебраических уравнений (СЛАУ).Координатная и матричная формы записи.Равносильность СЛАУ.

12.Теорема Кринекера-Капелли о совместности СЛАУ.Решение СЛАУ с помощью обратной матрицы.Крамер.Гаусс.Критерий определен.слау

13.Решение однородных СЛАУ.Критерий существования ненулевого решения. Фундаментальная система.

14.Декартова прямоуг.система координат.Линейные операции над векторами.Вычисление длины вектора.

№15.Опр скал-ого произв-я. Его св-ва. Вывод формулы скал пр. Признак ортогональности векторов. Ортог проекция вект-а на ось.

№16.Правые и левые тройки геометр-их вект-ов. Опред вектор-ого произв-я.Его св-ва.Признак коллин-сти.

№17.Определение смешанного произведения трех векторов. Его св-ва. Признак компланарности 3 векторов. Нахождение объема тетраэдра.

№18. Уравнение прямой, проходящей через две данные точки. Уравнением прямой с угловым коэф-от. Уравнение прямой в отрезках.

№18 Уравнение прямой, проходящей через две данные точки. Взаимное расположение прямых на плоскости. Условия пар-сти и перпендикулярности прямых. Расстояние от точки до прямой. Нормальный вектор. Направляющий вектор. Каноническое уравнение. Параметрическое уравнение. Нормальное уравнение прямой на плоскости.

№19. Общее уравнение плоскости. нормальным вектором. общим уравнением плоскости. Условием пар-ости двух плоскостей. Нормальным уравнением плоскости. Расстояние от точки до плоскости. Уравнение плоскости проходящей через три точки. Уравнение плоскости проходящей через три точки.

каноническое уравнение прямой. параметрические уравнения прямой.

21.Взаимное расположение L и П. Угол между L и П.

Расстояние от точки L до v3.

22.Кривые второго порядка на плоскости:эллипс, гипербола,парабола. Определения,вывод их канонических ур-ий.Фокусы,эксцентриситет,директр.

23.Общие ур-ие кривых второго порядка на плоскости. Инварианты кривых второго порядка на плоскости.Классификация и виды каноническихь ур-ий(9)кривых второго порядка.

24.Поверхности второго порядка.Эллипсоиды,гиперболоиды,Параболоиды, цилиндры,конусы.Канонич.ур-я.Инварианты.

25.Линейные операторы в линейном пространстве. Матрица линейного оператора.

26.Преобразование координат вектора при переходе к новому базису. Изменение координат вектора при изменении базиса.

27.Собственные векторы и собственные значения линейного оператора. Характеристический многочлен линейного оператора.