
Математика. Шпоры
.doc
|
10.Линейное пространство решений однородного линейного ОДУ n-ого порядка, его размерность. ФСР линейного однородного ОДУ n-ого порядка. Линейным дифференциальным уравнением n –го порядка называется уравнение вида y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x). Коэффициенты уравнения an-1(x), an-2(x), ..., a1(x), a0(x) и правую часть f(x) полагаем непрерывными на отрезке [a;b] . y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x) — неоднородное линейное дифференциальное уравнение n–го порядка, y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0 — однородное линейное дифференциальное уравнение n–го порядка, Выражение в левой части уравнения называется линейным дифференциальным оператором n –го порядка: L(y) ≡ y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y. L(y) = 0 и L(y) = f(x) — соответственно однородное и неоднородное уравнения в операторной записи. При изучении линейных дифференциальных уравнений используются пространства C[a;b] — пространство непрерывных на отрезке [a;b] функций, и Ck [a;b] — пространство функций, непрерывных на [a;b] , вместе со своими производными до k –го порядка включительно. Рассмотрим линейное однородное дифференциальное уравнение y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0. Фундаментальной системой решений однородного линейного дифференциального уравнения называется упорядоченный набор из n линейно независимых решений уравнения. Иными словами любые n линейно независимых решений y1(x), y2(x),..., yn(x) уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0 образуют фундаментальную систему решений. Доказано, что у однородного линейного дифференциального уравнения с непрерывными коэффициентами существует фундаментальная система решений. Пусть задана некоторая линейно независимая система n векторов из Rn:
И пусть функции y1(x), y2(x),..., yn(x) — решения линейного однородного уравнения с начальными условиями:
|
Функции y1(x), y2(x),..., yn(x) образуют фундаментальную систему решений линейного однородного уравнения. Рассмотрим на [a; b] линейное однородное дифференциальное уравнение y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0. Общим решением этого уравнения на отрезке [a;b] называется функция y = Φ(x, C1,..., Cn ), зависящая от n произвольных постоянных C1,..., Cn и удовлетворяющая следующим условиям : − при любых допустимых значениях постоянных C1,..., Cn функция y = Φ(x, C1,..., Cn ) является решением уравнения на [a; b] ; − какова бы ни была начальная точка (x0, y0, y1,0 ,..., yn − 1,0 ) , x0∈ [a;b] , существуют такие значения C1 =C10 , ..., Cn = Cn0 , что функция y = Φ(x, C10 , ..., Cn0) удовлетворяет начальным условиям y(x0) = y0, y '(x0) = y1,0 ,..., y(n − 1) (x0) = yn− 1,0 . Справедливо следующее утверждение ( теорема о структуре общего решения линейного однородного уравнения). Если все коэффициенты уравнения линейного однородного дифференциального уравнениния непрерывны на отрезке [a;b] , а функции y1(x), y2(x),..., yn(x) образуют фундаментальную систему решений этого уравнения, то общее решение уравнения имеет вид y(x,C1,..., Cn) = C1 y1(x) + C2 y2(x) + ... + Cn yn(x), где C1,...,Cn — произвольные постоянные.
фундаментальную систему решений которого образуют функции y1(x) = ln x , y2(x) = x. Общим решением уравнения является функция y(x, C1, C2) = C1 ln x + C2x.
|
|
11.Формула Лиуви́лля-Острогра́дского — формула, связывающая определитель Вронского (вронскиа́н) для решений дифференциального уравнения и коэффициенты в этом уравнении. Пусть есть дифференциальное уравнение вида y(n) + P1(x)y(n − 1) + P2(x)y(n − 2) + ... + Pn(x)y = 0,
тогда Для линейной однородной системы дифференциальных уравнений y'(x) = A(x)y(x), где A(x) — непрерывная квадратная матрица порядка n, справедлива формула Лиувилля-Остроградского
Правило дифференцирования определителя размерности n
Пусть Тогда для производной Δ'(x) верно
(в i-м слагаемом продифференцирована i-я строка)
|
Доказательство Воспользуемся формулой полного разложения определителя
Дифференцируя это выражение по x, получим
В каждой сумме продифференцированы элементы i-й строки и только они. Заменив суммы определителями, получим
|
|
15.Теорема о ФСР для линейного однородного ОДУ n-ого порядка с постоянными коэффициентами. Фундаментальная система решений (ФСР) представляет собой набор линейно независимых решений однородной системы уравнений.
Совокупность
любых двух линейно независимых на
интервале (a; b) частных решений
Теорема (о ФСР)
Если
два частных решения
Линейное однородное уравнение n-го порядка с постоянными коэффициентами Уравнение n-го порядка для одной неизвестной функции z независимого переменного t с постоянными коэффициентами имеет вид:
(2.1) где a1,ј,an - постоянные числа (действительные или комплексные). К уравнению (2.1), очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось. Решения уравнения (2.1) будут построены в явном виде и тем самым установлена еще раз теорема существования. Теорема единственности будет использоваться по существу для доказательства того, что найдены все решения данного уравнения. Прежде, чем приступить к решению уравнения (2.1) условимся о некоторых обозначениях и понятиях. Производную по времени от произвольной функции z = z(t) удобно обозначать через pz = p(z), трактуя символ p как линейную операцию над функцией z:
(2.2)
Тогда
натуральная степень k операции p,
обозначаемая через pk,
естественно понимается как
и представляет собой производную k-го порядка от функции z:
(2.3) Ясно, что степень pk операции p подчиняется формальным алгебраическим правилам
|
Естественным представляется определение операции cpk, где c - число и суммы pk + pm:
(2.4) Пользуясь введенными обозначениями, мы можем записать левую часть уравнения (2.1) в виде
(2.5) Положим
Данное выражение в соответствии с равенством (2.5) представляет собой линейную операцию над функцией z, т.е.
С другой стороны само выражение (2.6) представляет собой выражение относительно символа p с постоянными (действительными или комплексными) коэффициентами, для которого справедливы обычные алгебраические правила оперирования, т.е. если L(p) и M(p) - два произвольных многочлена относительно символа p (или, как говорят, оператора дифференцирования p), то
Предложение 2.1.1 Если L(p) -многочлен относительно оператора дифференцирования вида (2.6), то справедлива следующая формула
(2.8) Здесь l - произвольное действительное или комплексное число;
Доказательство. Мы имеем
Отсюда
следует, что
Из формулы (2.8) следует, что функция elt является решением уравнения (2.1), т.е.
тогда и только тогда, когда число l есть корень многочлена L(l), т.е. L(l) = 0.
|
|
20.Определитель Вронского Определителем Вронского W(x; y1(x), y2(x), ..., yn(x)) называется определитель, первая строка которого образована функциями y1(x), y2(x), ..., yn(x) из Cn-1[a, b] , а последующие строки образованы производными от функций предыдущей строки:
Справедливо следующее необходимое условие линейной зависимости функций. Если функции y1(x), y2(x), ..., yn(x) линейно зависимы на отрезке [a;b], то их определитель Вронского тождественно равен нулю на этом отрезке: W(x; y1(x), y2(x), ..., yn(x)) ≡ 0 на [a;b]. Важно понимать, что обратное утверждение неверно. Определитель Вронского линейно независимой системы функций может быть тождественно равен нулю. Однако, если определитель Вронского системы функций на некотором отрезке отличен от тождественного нуля, то система функций линейно независима на этом отрезке. Вычислим на всей числовой оси определитель Вронского W(x;1, x, x2,..., xn) — определитель Вронского системы функций 1, x, x2,..., xn.
Определитель Вронского на всей числовой оси отличен от нуля, следовательно функции 1, x, x2,..., xn линейно независимы на всей числовой оси. Определитель Вронского линейно независимой системы функций может быть тождественно равен нулю. Рассмотрим две функции:
|
Эти функции линейно независимы на [0, 2]. Действительно:
Вычислим определитель Вронского W(x; y1(x), y2(x)) на [0, 2]:
Итак, функции линейно независимы на [0, 2], а W(x; y1(x), y2(x)) ≡ 0 на [0, 2]. Этот пример означает, что тождественное равенство нулю определителя Вронского системы функций является необходимым условием линейной зависимости системы функций, но не является достаточным условием линейной зависимости системы функций. С другой строны, отличие от тождественного нуля определителя Вронского системы функций является достаточным условием условием линейной независимости системы функций. (Ведь если бы она была бы линейно зависима, то определитель Вронского был бы тождественным нулём). Определителем Вронского вектор-функций Y1(x), Y2(x), ..., Yn(x),
называется определитель W[x; Y1, Y2, ..., Yn], заданный равенством
|
|
21.СТРУКТУРА ОБЩЕГО РЕШЕНИЯ НЕОДНОРОДНОЙ СИСТЕМЫ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Рассмотрим неоднородную линейную систему обыкновенных дифференциальных уравнений n-го порядка
Здесь
Справедлива следующая теорема о структуре общего решения этой неоднородной линейной системы ОДУ. Если матрица A(x) и вектор-функция b(x) неперерывны на [a, b], и пусть Φ(x) — фундаментальная матрица решений однородной линейной системы Y' = A(x)Y , то общее решение неоднородной системы Y' = A(x)Y + b(x) имеет вид:
|
Из приведенной формулы легко получить формулу решения задачи Коши для линейной неоднородной системы ОДУ — формулу Коши. Решением задачи Коши Y' = A(x)Y + b(x), Y(x0) = Y0 является вектор-функция
Принцип суперпозиции: Если y1(x) и y2(x) — решения неоднородных линейных уравнений L(y) = f1(x) и L(y) = f2(x), то их сумма y(x) = y1(x) + y2(x) является решением уравнения L(y) = f1(x) + f2(x).
|
|
22.Метод вариации постоянных для поиска частного решения линейной неоднородной системы ОДУ. Задача состоит в вычислении какого–либо частного решения линейного неоднородного дифференциального уравнения с непрерывными коэффициентами и непрерывной правой частью. Рассмотрим линейное неоднородное дифференциальное уравнение y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x). с нерерывными на [a; b] коэффициентами и непрерывной правой частью. Предположим, что известна фундаментальная система y1(x), y2(x),..., yn(x) решений соответствующего однородного уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0. Будем искать частное решение неоднородного уравнения в виде y*(x) = C1(x) y1(x) + C2(x) y2(x) + ... + Cn(x) yn(x) , где C1(x), C2(x) , ... , Cn(x) — неизвестные, n раз дифференцируемые на [a; b] функции. Их называют варьируемые постоянные общего решения однородного уравнения. Справедливо следующее утверждение. Пусть y1(x), y2(x),..., yn(x) — фундаментальная система решений однородного уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0 с непрерывными на отрезке [a; b] коэффициентами. Если правая часть f(x) неоднородного уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x) непрерывна на [a; b], то его частное решение можно искать в виде y*(x) = y(x,C1,..., Cn) = C1(x) y1(x) + C2(x) y2(x) + ... + Cn(x) yn(x) .
|
Неизвестные функции C1(x), C2(x) , ... , Cn(x) находятся из системы
Такой метод отыскания частного решения неоднородного уравнения называется методом вариации произвольных постоянных или методом Лагранжа.
|
|
12Понижение
порядка линейного однородного
уравнения, если известно одно его
частное решение. Пусть
для линейного уравнения |
|
|
12.Восстановление
линейного однородного уравнения по
фундаментальной системе решений. Пусть
дана система функций y1(x), y2(x),
…, yn(x) с
отличным от нуля на
отрезке (a,b) вронскианом W(x).
Требуется составить линейное
однородное уравнение,
у которого фундаментальная система
решений состоит из функций y1(x), y2(x),
…, yn(x).
|
Заметим,
что коэффициент при старшей производной
оказывается равным вронскиану
фундаментальной система
решений:
|
|
13) Структура общего решения линейного неоднородного ОДУ n-ого порядка. Рассмотрим на [a; b] линейное однородное дифференциальное уравнение y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0. Общим решением этого уравнения на отрезке [a;b] называется функция y = Φ(x, C1,..., Cn ), зависящая от n произвольных постоянных C1,..., Cn и удовлетворяющая следующим условиям : − при любых допустимых значениях постоянных C1,..., Cn функция y = Φ(x, C1,..., Cn ) является решением уравнения на [a; b] ; − какова бы ни была начальная точка (x0, y0, y1,0 ,..., yn − 1,0 ) , x0∈ [a;b] , существуют такие значения C1 =C10 , ..., Cn = Cn0 , что функция y = Φ(x, C10 , ..., Cn0) удовлетворяет начальным условиям y(x0) = y0, y '(x0) = y1,0 ,..., y(n − 1) (x0) = yn− 1,0 . Справедливо следующее утверждение ( теорема о структуре общего решения линейного однородного уравнения): Если все коэффициенты уравнения линейного однородного дифференциального уравнения непрерывны на отрезке [a;b] , а функции y1(x), y2(x),..., yn(x) образуют фундаментальную систему решений этого уравнения, то общее решение уравнения имеет вид y(x,C1,..., Cn) = C1 y1(x) + C2 y2(x) + ... + Cn yn(x), где C1,...,Cn — произвольные постоянные. Метод вариации постоянных для поиска частных решений линейного неоднородного ОДУ n-ого порядка. Задача состоит в вычислении какого–либо частного решения линейного неоднородного дифференциального уравнения с непрерывными коэффициентами и непрерывной правой частью. Рассмотрим линейное неоднородное дифференциальное уравнение y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x). с непрерывными на [a; b] коэффициентами и непрерывной правой частью. Предположим, что известна фундаментальная система y1(x), y2(x),..., yn(x) решений соответствующего однородного уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0. Будем искать частное решение неоднородного уравнения в виде y*(x) = C1(x) y1(x) + C2(x) y2(x) + ... + Cn(x) yn(x) , где C1(x), C2(x) , ... , Cn(x) — неизвестные, n раз дифференцируемые на [a; b] функции. Их называют варьируемые постоянные общего решения однородного уравнения.
|
Справедливо следующее утверждение. Пусть y1(x), y2(x),..., yn(x) — фундаментальная система решений однородного уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0 с непрерывными на отрезке [a; b] коэффициентами. Если правая часть f(x) неоднородного уравнения y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = f(x) непрерывна на [a; b], то его частное решение можно искать в виде y*(x) = y(x,C1,..., Cn) = C1(x) y1(x) + C2(x) y2(x) + ... + Cn(x) yn(x) . Неизвестные функции C1(x), C2(x) , ... , Cn(x) находятся из системы
Такой метод отыскания частного решения неоднородного уравнения называется методом вариации произвольных постоянных или методом Лагранжа.
|


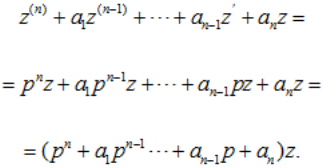
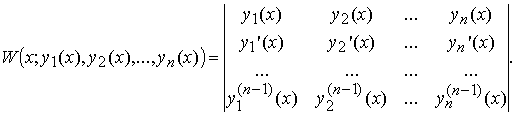
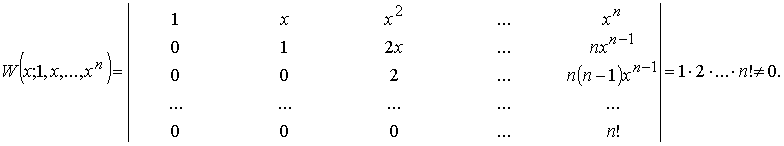
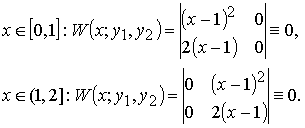
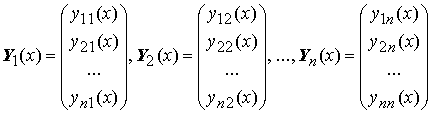
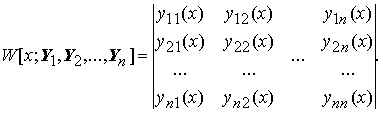
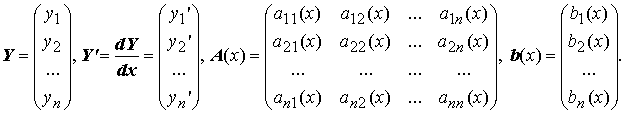
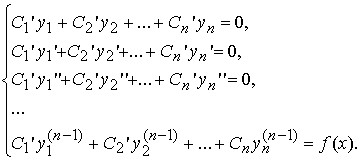
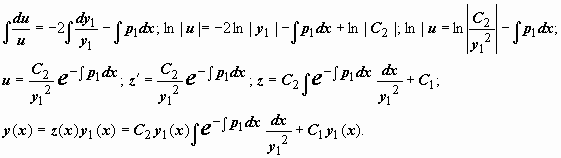 Можно
доказать, что вронскиан системы
функций
Можно
доказать, что вронскиан системы
функций 

